Portale "Ingegneria e Campanologia" - Autore - Sommario - Mappa del Sito - Home
Enciclopedia di Didérot e D'Alembert
AREA II - ARCHIVIO STORICO (ARS)
Cap. ARS-D01 - Arte della fusione delle campane - Pag. ARS-D01.04
Gli argomenti trattati sono stati inseriti da Ing. Arch. Michele Cuzzoni nel 2012 - © Copyright 2007- 2025- e sono desunti dalla documentazione indicata in Bibliografia a fondo pagina
|
Sviluppo della trattazione |
|||||||||||
| Pag. 1 | Pag. 2 | Pag. 3 | Pag. 4 | Pag. 5 | Pag. 6 | Pag. 7 | Pag. 8 | Pag. 9 | Pag. 10 | Pag. 11 | Pag. 12 |
| Quadro | Immagini | Traduzione | Immagine | Immagine | Immagine | Immagine | Immagine | Immagine | Immagine | Immagine | Traduzione |
| Sei qui | |||||||||||
Tavola grafica 1 - Disegno del campione e del Diapason
Tavola grafica (planche) 1 - Disegno del campione e del diapason
Tavola I. Disegno
del campione e del diapason
Fig. 1 - primo pezzo del campione, per la descrizione del quale si sono
usati 30 bordi
Fig. 4 - diapason geometrico, per trovare i diametri convenienti a tutti gli
intervalli
Tavola grafica (planche) 1 - Disegno del campione e del diapason
Traduzione dal francese
antico a cura di Ing. Arch. Michele Cuzzoni
[...] Il testo presentato
nella traduzione tra parentesi quadre in rosso è un commento del traduttore.
(...) Il testo presentato nella traduzione tra parentesi
rotonde in turchese è un completamento della versione italiana per renderla
più comprensibile.
L’Encyclopédie ou Dictionnaire raisonné des sciences, des
arts et des métiers, opera monumentale diretta dal filosofo Denis
Diderot
(1713-1784) e dal matematico Jean-Baptiste d’Alembert
(1717-1783), rappresenta probabilmente la più straordinaria utopia del
secolo dei Lumi; secolo che di utopie ne produsse molte e che dietro la
chiarezza cristallina delle sue enunciazioni nascondeva i forti
antagonismi che in Francia sfociarono nella Rivoluzione. Oltre ai 21 volumi di testo, il progetto conta ben 12
volumi di immagini che compongono la Raccolta di tavole, le
celebri
planches incise su lastre di rame
pubblicate nell’arco di oltre tre decenni, tra il 1746 e il 1780, con
una tiratura di ben 4250 copie (decisamente elevata per l’epoca e per
un lavoro di tale portata). Se l’opera non naufragò definitivamente – come aveva più
volte rischiato di fare, sommersa da innumerevoli difficoltà e oggetto di
feroci ostilità soprattuto da parte delle autorità ecclesiastiche – lo
si deve anche a collaboratori del tutto fuori del comune. Uno su tutti:
Louis-Jacques Goussier (1722-1799), personaggio eclettico e
preparatissimo, a un tempo fisico, matematico e pittore. «Non solo Goussier era abile nel rimaneggiare le
tavole tratte da raccolte varie – scrive lo storico Jacques Proust –
accertando talora sul posto questo o quel particolare. Su richiesta di
Diderot, condusse anche una serie di ricerche in provincia. Trascorse così sei
settimane nella cartiera di Montargis, un mese nella
fonderia di ancore di Cosne-sur-Loire, sei mesi in totale nella
Champagne e in Borgogna per studiare le grosse fucine e le fabbriche di specchi.
Prese schizzi sul posto, si fece spiegare dagli stessi imprenditori le
attrezzature, le macchine e il loro funzionamento».1 Preso in forze da d’Alembert, Goussier probabilmente è già
vicino a Diderot nel 1749 quando questi tenta di coordinare i lavori di
preparazione dell’Encyclopedie
dalla cella di Vincennes, ove era stato rinchiuso (per la verità sotto regime
piuttosto blando) per via di alcuni suoi scritti. Ed è a Goussier che si deve
non solo la realizzazione di gran parte dei disegni preparatori per le
planches 2, ma
anche la redazione di numerosi testi esplicativi che corredano
le immagini e, cosa non meno importante, i lavori di coordinazione e di
supervisione dell’intera Raccolta. Ne risulta che i testi redatti da Goussier come spiegazione
delle tavole da lui stesso disegnate, figli entrambi di una ricerca sul
campo anziché di compilazioni da lavori precedenti, spesso evidenziano
un più alto livello di ricerca rispetto ai corrispettivi lemmi presenti nei
volumi di testo della stessa Enciclopedia. È il caso, ad esempio, del suo
piccolo trattato sulla
Forgiatura delle ancore, o quelli sulla
Fusione delle campane o sulla Stampa delle
incisioni su rame. L’utopia sulla quale si fonda l’Encyclopedie è erede
di quel pensiero affermatosi dopo la scoperta del Nuovo Mondo – e coltivato
soprattutto dai grandi scienziati naturalisti del XVI secolo,
come
Leonhard Fuchs (1501-1566), Conrad Gessner (1516-1565)
e Ulisse Aldrovandi (1522-1605) – secondo il quale l’intero
universo biologico, gli animali e i vegetali, come pure il regno minerale,
potesse essere racchiuso per intero nel Grande libro della natura.
Entro il quale, secondo la loro idea tanto affascinante quanto irrealizzabile
(col senno di poi), ogni cosa avrebbe trovato una sua collocazione chiara e
definita in un casellario ideale; ordinata, descritta e, come si diceva,
picta (dipinta), poiché le immagini sono in grado
di mostrare ciò che le parole, per loro natura, non dicono, assurgendo
a elemento non già decorativo ma di conoscenza. La Raccolta di tavole che accompagna i volumi di
testo è una straordinaria utopia proprio perché «tutto in essa è
trasparente, limpido, senza mistero. È tutto è segno. I muri delle
fabbriche, dei laboratori, delle botteghe vengono abbattuti per mostrarci quanto
di solito vi si fa fuori della vista dei passanti. Per questo le tavole
non si possono leggere senza le spiegazioni che le corredano, e viceversa.
Viste e lette insieme, fanno vedere l’universo naturale e il mondo degli
artefatti creati ed impiegati dall’uomo, nella loro realtà, senza aggiungervi né
togliervi niente. Così concepita, naturalmente, la Raccolta di tavole
dell’Enciclopedia non poteva essere che un’utopia: pura illusione la sua
perfetta leggibilità, la sua malia è quella d’una illusoria certezza»3. Con il tempo, il fallimento della pretesa di dominare tutte
le cose per mezzo della ragione e il riconoscimento dei limiti dei
propri strumenti di pensiero, diverrà un punto di forza decisivo per
l’avanzamento delle conoscenze, dove pure a fronte di conquiste straordinarie si
arriverà a
riconoscere la parzialità dei propri modelli e la loro provvisorietà.
Ecco dunque che diviene di primaria importanza proprio la condivisione dei
saperi, perché possano fornire una base solida sulla quale costruire – e
ricostruire – un presente e un futuro. Diderot delinea assai chiaramente gli obiettivi e la
ragion d’essere dell’Encyclopedie nella voce
omonima dell’opera, quegli stessi obiettivi che lo spronano a portare a termine
il progetto, sia pure tra mille difficoltà, anche dopo che molti collaboratori,
compreso lo stesso d’Alembert, decidono di abbandonarlo: «Questa parola significa ‘concatenazione delle
scienze’, essendo composta dalla preposizione greca in
e dai sostantivi greci circolo e
conoscenza. Scopo di un’enciclopedia è infatti raccogliere
le conoscenze sparse sulla faccia della terra, esporne ai nostri
contemporanei il sistema generale e trasmetterle ai posteri, affinché l’opera
dei secoli passati non sia stata inutile per i secoli a venire; affinché i
nostri nipoti, resi più istruiti, diventino nello stesso tempo più
virtuosi e felici; e affinché noi non dobbiamo morire senza aver ben
meritato del genere umano». 1) Jacques Proust, Il recueil de
planches dell’Encyclopédie, in
L’Encyclopédie di Diderot e d’Alembert. Tutte le tavole,
prefazione di Piergiorgio Oddifredi, saggi introduttivi di Jacques Proust, note
e commenti alle tavole di Giancarlo Buzzi, Arnoldo Mondadori Editore, Milano
2009, p. 12. 2) Contando i numerosissimi disegni a firma
di Goussier e quelli che firmati non sono ma che pure vanno attribuiti a lui, si
può stimare che egli complessivamente realizzò i disegni di circa i due terzi di
tutte le 2.500 planches dell’Encyclopedie, affidando poi ad
altri collaboratori il compito di tradurli in incisioni su rame (calcografia)
per la stampa. 3) Jacques Proust, cit., p. 14.
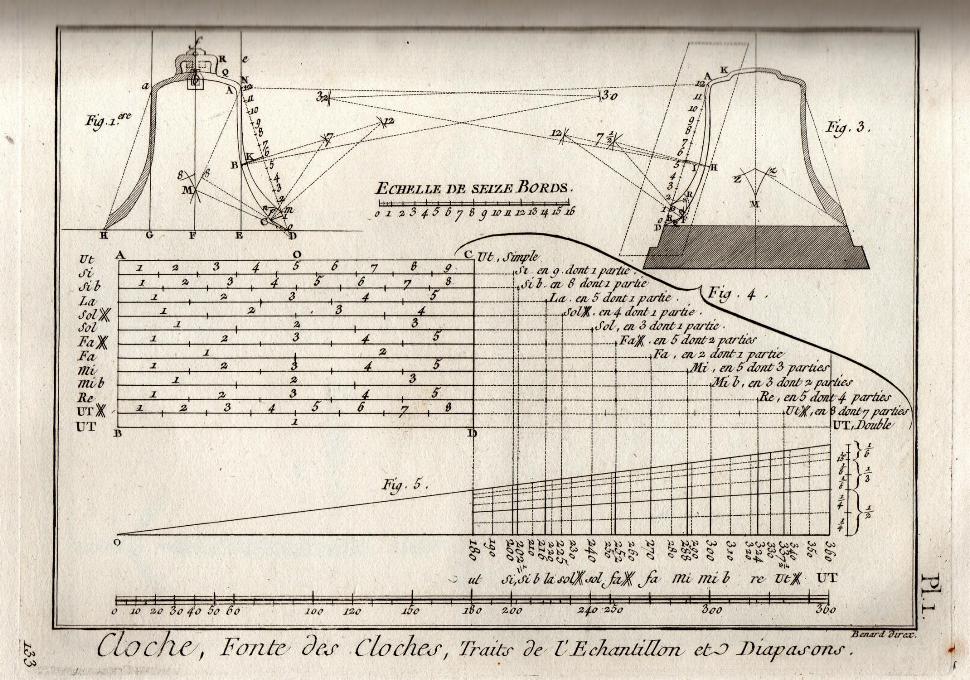
Figura 01 - Tavola 1 - Costruzione geometrica del modello e schema per ottenere
la nota desiderata
La sagoma (nell'originale échantillon) è un calibro, che nella forma dei suoi tratti rappresenta il profilo di una campana, e che essendo montato sul suo albero, fa le veci di un grande compasso girevole, per dare agli stampi la vera figura del di sotto e del di sopra di una campana.
Questo strumento rappresentato dalla
![]() fig. 3 della tavola
seguente, è una sagoma di noce, melo o altro legno pulito e liscio, a cui si
danno per altezza 12 bordi
della campana di cui essa deve essere il calibro, e
5 bordi per larghezza [il
termine "bordo" si rifà alla scala graduata dei "16 bordi" vista nella tavola
soprastante].
fig. 3 della tavola
seguente, è una sagoma di noce, melo o altro legno pulito e liscio, a cui si
danno per altezza 12 bordi
della campana di cui essa deve essere il calibro, e
5 bordi per larghezza [il
termine "bordo" si rifà alla scala graduata dei "16 bordi" vista nella tavola
soprastante].
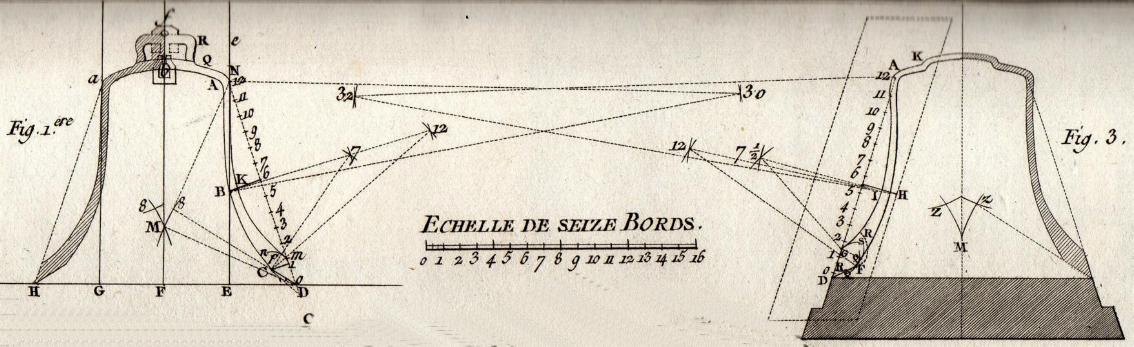
Figura 02 - Dettaglio Tavola 1 - Costruzione geometrica del modello
(Facendo riferimento alla posizione situata) a due
bordi
(alla distanza cioè di due posizioni) del suo bordo
vivo a destra, si tira col misuratore di marcatura
(righello) una linea molto leggera da un capo all'altro, sulla quale si
indicano 14 o 15 bordi, cominciando dal basso, di cui i primi due o tre
sono destinati alla base degli stampi (che si chiamano la sagoma nel termine
dell'arte), e gli altri 12 sono impiegati per ricercare le forme del calibro;
perché le campane devono avere nella loro altezza 12 bordi, dal punto D al punto
A [Vedi figura soprastante].

Figura 03 - Dettaglio Tavola 1 - Costruzione geometrica del modello
- Sia la linea A0, divisa in 12 bordi meno 1/6
(di bordo), - e questo 1/6
(di bordo) collegato da 0 in D, per completare i 12
bordi, e per fare il morsetto della campana in D; - siano
anche 6 piccole linee puntinate, facenti squadra con la linea A0;
- la prima al numero 1 e mezzo,
- la seconda al numero 3, - la terza
al numero 5 e mezzo,
- una al numero 6, - una al numero
11, - l'ultima al numero 12 e 1/6.
La prima, la terza e l'ultima a partire dal punto 0, serviranno a fare il
campione, e le altre a fare la verifica.
Poiché il luogo del grande cavo (interno) è
il terzo indicato al numero 3, - si deve contare 2/3
del bordo nel suo spessore, - si deve portare 1/3 e 1/15 di
bordo di spessore, - e lo spessore che è al numero 11, deve
portare 1/3 di bordo.
Figura 04 - Dettaglio Tavola 1 - Costruzione geometrica del
modello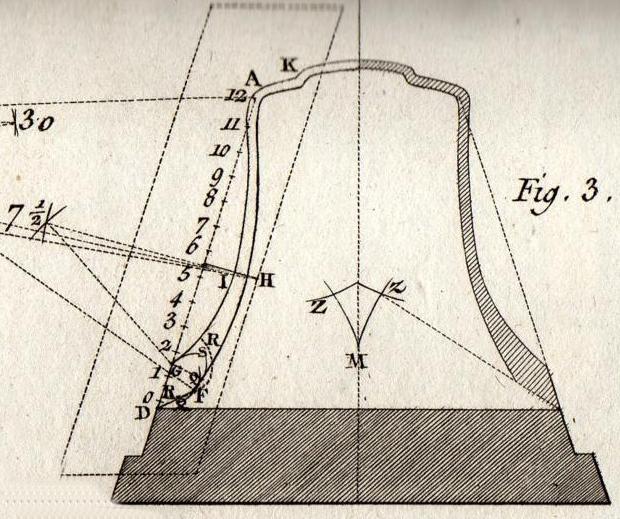
Questi 3 spessori, dopo aver fatto la verifica, devono incontrarsi giusti
con l'operazione (di costruzione), se è
stata fatta esattamente, diversamente bisogna ricominciare.
Le cose sono così disposte: - si prende nel compasso 1/6 di
bordo che si porta dal numero 1 e 1/2 in G (nella figura
in alto), e dal punto 0 in D.
- Di questo passo il punto G si troverà scartato dalla
linea A0 di 1/6 di bordo; - dopo ciò, e fino a quando
si sarà aperto il compasso dell'ampiezza di un bordo e 1/2, uno dei punti posati
sul punto 5 e 1/2,
- l'altro punto darà sulla perpendicolare il punto H:
- poi tenendo il compasso chiuso alla quota di 1/3 + 1/15
[= 6/15 = 2/5] di bordo, si porterà questa lunghezza dal punto H in I, e
per HI si creerà il punto di "flesso" e
(la posizione del) ripieno o della nota
nominale della campana.
Figura 05 - Dettaglio Tavola 1 - Costruzione geometrica del
modello
Si apre il compasso di 1 bordo e 1/15 di bordo [= 16/15]
: - si pone uno dei bracci sul punto G, e dall'altro si fa
il piccolo arco RR;
- poi dal numero 1, l'altro piccolo arco QQ;
- e dal punto di intersezione F di questi due archi, come centro, si forma
la figura SGI; - poi si tira la diagonale FD, che con
D, G, darà il grande bordo.
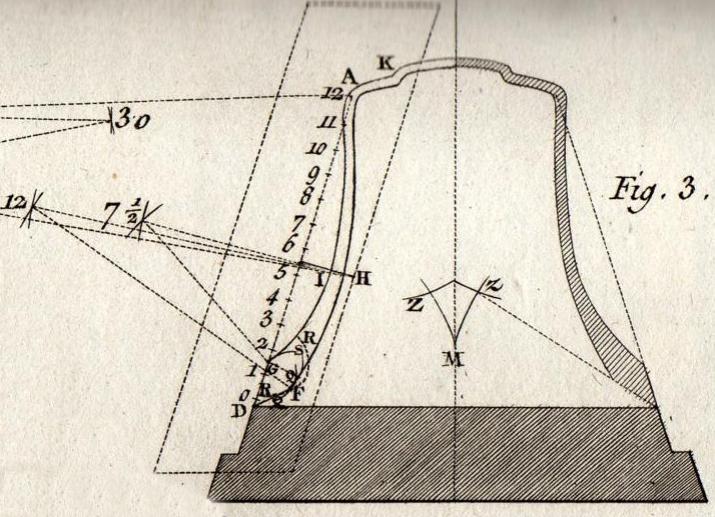
Figura 06 - Dettaglio Tavola 1 - Costruzione geometrica del modello
- Si dà al compasso un'apertura di 12 bordi: - dal punto
H si va costruendo un piccolo arco a sinistra fuori della base dello stampo;
- dal punto F, un altro piccolo arco che, per sua intersezione con l'arco
precedente, darà il centro di curvatura HF. - Si
apre quindi il compasso per un'ampiezza di 7 bordi e 1/2; -
e dal punto I, poi dal punto G, si fanno due piccoli archi fuori dello stampo
anch'essi a sinistra, da cui, e dalla loro comune intersezione presa come
centro, si traccia l'altra curva IG: ed ecco tracciato il vaso inferiore.
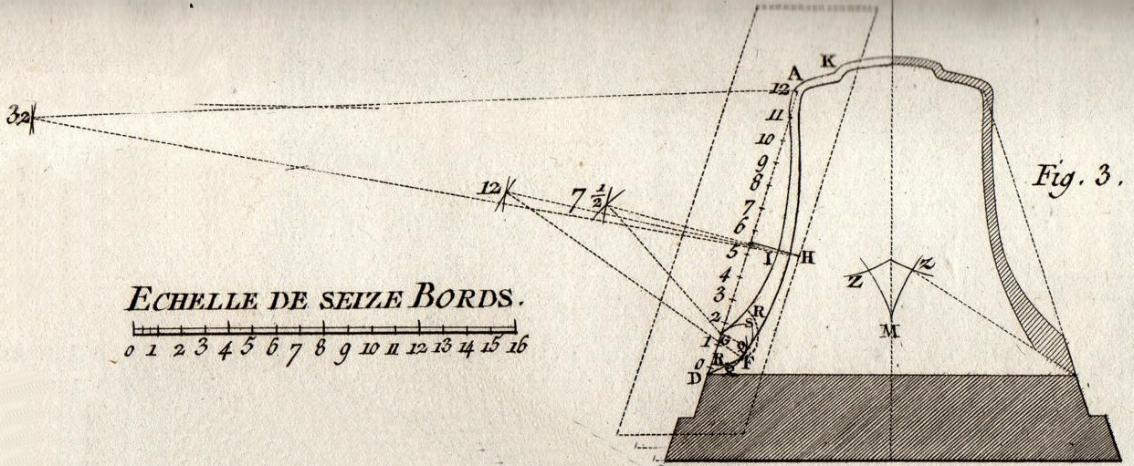
Figura 07 - Dettaglio Tavola 1 - Costruzione geometrica del modello
- Si apre il compasso di 32 bordi, avendolo messo su H e su L,
- si tracciano due archi fuori dello stampo a sinistra; -
dal punto ove essi si intersecano, si forma il tratto HL;
- in seguito e senza cambiare l'apertura, si pone un capo su K e su I, per
avere parallelamente due archi e un centro comune, da cui si tira
l'ultima curva KI: e il vaso superiore è fatto.
Figura 08 - Dettaglio Tavola 1 - Diapason geometrico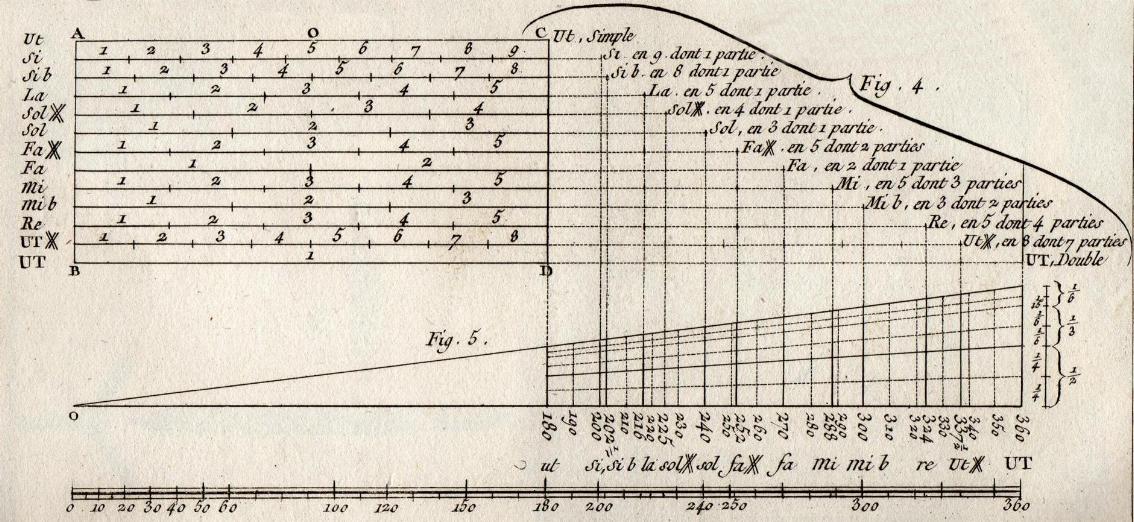
| Tono | Proporzione |
| Tono unisono è in proporzione di | 1 a 1 |
| La seconda maggiore è in proporzione di | 9 a 8 |
| La seconda minore è in proporzione di | 10 a 9 o di 16 a 15 |
| La terza maggiore è in proporzione di | 5 a 4 |
| La terza minore è in proporzione di | 6 a 5 |
| La quarta è in proporzione di | 4 a 3 |
| La quinta è in proporzione di | 3 a 2 |
| La sesta maggiore è in proporzione di | 5 a 3 |
| La sesta minore è in proporzione di | 8 a 5 |
| La settima maggiore è in proporzione di | 9 a 5 |
| L'ottava è in proporzione di | 2 a 1 |
| Tono | Proporzione |
| La nona maggiore è in proporzione di | 9 a 4 |
| La nona minore è di 32 a 15 o di | 20 a 9 |
| La decima maggiore è di | 5 a 2 |
| La decima minore è di | 12 a 5 |
| La undicesima è in proporzione di | 8 a 3 |
| La dodicesima è in proporzione di | 3 a 1 |
| La tredicesima maggiore è di | 10 a 3 |
| La tredicesima minore è di | 16 a 5 |
| La quattordicesima maggiore è di | 15 a 4 |
| La quattordicesima minore è di | 18 a 5 |
| La doppia ottava è di | 4 a 1 |
E' su questa tavola che tutti i
fonditori devono basare il loro lavoro; essa contiene i principi da dove
(si) devono dedurre non solo le leggi dell'eleganza e del buon gusto, ma
quelli del vero e del necessario. Si può lo stesso affermare
che senza questa specie di vademecum, non si può trovare né accordi, né armonie,
né pesi, né spessori, né diametri, se non per puro azzardo.
Così quella è la base di tutto.
Figura 09 - Dettaglio Tavola 1 - Diapason geometrico
Per fare uso di questa tabella, bisogna
tracciare 12 linee parallele e perpendicolari alle due linee AB, CD. Queste
parallele rappresentano tutti i diametri del do acuto.
In seguito a ciò, per trovare i diametri delle altre 11 campane, bisogna
dividere tutte queste perpendicolari in questa maniera.
1) Si divide la linea AC nel suo uguale, che è al di sotto,
in 9 parti uguali di cui una parte è stata portata al prolungamento sulla linea
del si, formerà 10 parti contro 9, e nello stesso tempo la proporzione 10
a 9 è quella del si, seconda minore. 2) La
stessa linea è divisa in 8 parti uguali, di cui l'una è portata fino al punto
del si bemolle, darà 9 parti contro 8, e tuttavia la proporzione del 9 a 8 è
quella della seconda maggiore.
3) La parallela seguente si divide in 5 parti, di cui una è stata portata al
punto la, darà il diametro di 6 parti al posto di 5, e formerà lo stesso, la
proporzione di 6 a 5, a cui appartiene la terza minore.
4) La parallela al di sotto, essendo divisa in 4 parti, e
una di queste è stata portata al sol diesis, darà la proporzione di 5 a 4,
questa è quella della terza maggiore o sol diesis.
5) La linea seguente sarà divisa in 3 parti, una terza sarà portata al punto del
sol, ciò che darà 4 parti per 3 al sol naturale, e per questo la proporzione di
4 a 3, che è quella della quarta.
6) Per il fa diesis, si divide la linea ACo il suo uguale in 5 parti: una quinta
parte porta 2 volte al di là del punto C, e darà insieme alla linea AC, il
diametro del fa diesis.
7) si divide la linea seguente in 2, di cui metà sarà
portata in fa, e si avranno 3 metà per 2, ove la proporzione è per conseguenza 3
a 2 per la quinta. 8) Per avere il
diametro del mi naturale, si dividono in 5 parti uguali la linea AC, si
prende una quinta parte che si porta 3 volte al punto mi, ciò che farà 8 parti
al posto di 5, e nello stesso tempo la proporzione sarà di 8 a 5 per la sesta
minore.
9) Quanto al mi bemolle, si divide la linea in 3, e senza cambiare l'apertura
del compasso lo si porta per 2 volte fino al punto del mi bemolle, per avere il
diametro di questa campana, e la proporzione di 5 a 3 per la sesta maggiore.
10) Per quel che concerne il re, si divide in 5 parti la
linea AC. La quinta parte che si riporta in seguito 4 volte al punto re, dà 9
parti al posto di 5, e la proporzione di 9 a 5 per il re, settima minore.
11) Per trovare il diametro del do diesis, si divide in 8 la
linea AC , e si riporta per 7 volte una parte fino al punto del do diesis, ciò
che dà 15 parti contro 8, e la proporzione di 15 a 8 per la settima maggiore.
12) Do grave B D U T, è il doppio della linea del do acuto
AC.
Si sarà curiosi di conoscere la ragione primitiva di questa tavola, e perché, per esempio, si mette la quinta in proporzione di 3 a 2 e l'ottava di 2 a 1; e perciò bisogna fare un monocordo [vedi spiegazione del monocordo pitagorico facendo clic qui], che non sarà altro che un regolo di legno diviso in 360 parti uguali di due linee ciascuna o circa, lunghe da 5 a 6 piedi.
Si monterà questo regolo con una corda flessibile o di latta, di tutta la lunghezza delle 360 divisioni.
Occorrerà anche una seconda corda dello stesso materiale della prima, della stessa lunghezza e spessore montata con lo stesso accordo all'unisono.
Questa corda sarà sempre pizzicata a vuoto e in tutta la sua lunghezza, mentre si colpirà la prima a destra o a sinistra del cavalletto mobile.
Lo strumento è così disposto e accordato.
Spostate il cavalletto sulla prima corda al numero 180, che ne è la metà; pizzicate a destra e a sinistra del cavalletto, e poiché la parte destra e la parte sinistra sono ugualmente 180 numeri ciascuna, esse vi daranno l'uno e l'altra un insieme in perfetto unisono, e nello stesso tempo la proporzione 1 a 1.
Per rendere ragione alle proporzioni della tabella occorre un principio. Questo principio è che la parità deve essere per rapporto pari alle differenze proporzionali che si trovano dentro alla seconda corda che suona sempre il tono grave, e le parti della prima corda che suonano il tono acuto di una parte, e le proporzioni armoniche della tabella. Cioè, pizzicate la prima corda ai due lati del cavalletto; questi due lati, che sono di 180 ciascuno, suoneranno il do acuto, e la seconda corda che è immaginata di 360, suonerà il do grave, ottava (grave) del do acuto; e ciò sarà per la proporzione di 2 a 1, o altrimenti due corde di 180 divisioni contro 360.
Ponendo quindi il cavalletto al numero 240, se si pizzica il lato 240, e la seconda corda che è vuota, otterrete una quinta ben formata, e contemporaneamente la proporzione di 3 a 2; ecco la prova. La quinta è al tono grave come 240 a 360, ora, tra 240 e 360 c'è una differenza proporzionale, che è di 120, ma 120 si trova 3 volte compreso in 360, e due volte in 240, che è una differenza di 3 a 2: dunque la quinta è anche in proporzione di 3 a 2 col suono grave.
Spostate da là il cavalletto al numero 270, pizzicate questa parte di corda, e nello stesso tempo la corda del suono grave, voi avrete una quarta, e la proporzione di 4 a 3.; poiché la differenza che si trova tra 360 e 270, si deve trovare dentro al suono grave e la quarta; ora questa differenza è di 90 divisioni, che sono 4 comprese in 360 e 3 in 270. La differenza del tono grave alla quarta è dunque di 4 a 3.
La terza maggiore troverà il suo posto al numero 288, di cui la differenza proporzionale fino a 360 è di 72 divisioni; questa differenza si trova 5 volte in 360 e 4 volte in 288: dunque la differenza proporzionale dal tono grave alla terza maggiore è di 5 a 4.
Il numero 300 sarà il posto del cavalletto per la terza minore, e la differenza di 360 da 300 sarà anche quella della corda intera con la terza; ora questa differenza, che è di 60, si trova compresa 6 volte in 360 e 5 volte in 300. La proporzione armonica di 5 a 6 è dunque quella della terza minore.
La seconda minore si trova sotto il cavalletto al numero 320. C'è un vuoto di 40 tra 360 e 320, che forma la differenza proporzionale di questi due numeri; è anche la differenza che bisogna trovare tra la corda e il vuoto e questa è la seconda maggiore. Ora, 40 è compreso 9 volte in 360 e 8 volte in 320; la proporzione della seconda maggiore è per conseguenza di 9 a 8.
La seconda minore si trova al numero 324; da 324 fino a 360, c'è una differenza di 36 che si trova 10 volte nella corda intera che si suppone lunga 360 e 9 volte nella parte della corda della grandezza di 324: è dunque la proporzione di 10 a 9 che appartiene a questa seconda minore.
La sesta maggiore è al numero 116, dove si sposta il cavalletto; fino a 360 c'è il numero 144 di differenza, ma affinché questa grandezza di 144 non si trova che due volte in quella di 360 con il resto di 72, e non si trova che una volta in quella di 216, con resto uguale di 72, e che quindi questa proporzione di 2 a 1 non si può fare la proporzione che si cerca, poiché quella è già la proporzione dell'ottava, si opererà con questo resto di 72, come se fosse la differenza; ora, in 360, quante volte sta 72? 5 volte; e quante in 216? 3 volte, e tutto senza resto. Da cui si conclude che la proporzione cercata è di 5 a 3.
E' al numero 225 che si deve mettere il cavalletto per ottenere la sesta minore, il cui numero lascia un vuoto di 135 fino a 360; il qual numero 135 non è che una volta in 235 con il resto di 90, e 2 volte con lo stesso resto in 360: ora la proporzione di 2 a 1, come abbiamo appena detto, non può che essere l'ottava. Bisogna allora operare sul resto di 90, come se fosse la differenza, e dire, in 360 quante volte sta 90? 4 volte senza resto; e in 225 quante volte sta 90? 2 volte con il resto di 45. Ma perché non si deve avere alcun resto che non sia comune a questi due numeri? 360 e 225, bisogna passare a una terza operazione, e agire normalmente con il resto 45: ora come questo resto sia contenuto 8 volte giuste e senza alcun resto in 360, e 5 volte giuste in 225, si concluderà che il rapporto di 8 a 5 è quello della sesta minore.
Giunti alla settima maggiore, dove il numero 192 avrà suonato questo tono, si opererà nello stesso modo che per la sesta maggiore; cioè che tra 192 e 360 c'è una distanza di corda che comprende 168 parti, e che questo numero 168, non è compreso che due volte in 360 col resto di 24, e una volta in 192, con lo stesso resto preciso, bisognerà operare su questo resto di 24, e vedere quante volte lo contengono i numeri 360 e 192; sono 15 volte nell'uno, e 8 volte nell'altro; ed è anche il risultato cercato, e per cui la settima maggiore è detta in proporzione di 15 a 8.
C'è infine la settima minore di cui ora si tratta; lei deve suonare al numero 200, e lasciare un intervallo di corda di 160 parti. Ora questa grandezza 200 non comprende quella di 160 che una volta sola con il resto di 40; e siccome la proporzione di 2 a 1 non è che per l'ottava, bisogna lavorare su questo resto di 40, che è una grandezza comune a quella di 360 e di 200, nello stesso modo che precedentemente, e vedere quante volte 40 si trova in 360 e in 200; sono 9 volte nell'uno e 5 volte nell'altro.; da cui risulta che la proporzione di 9 a 5 è giustamente il valore cercato. Si è detto tutto per la prima ottava, e per ciò che riguarda la tesi dimostrativa delle proporzioni armoniche enunciate nella tabella.
E' per la differenza dei battimenti d'aria che si giunge a questa conoscenza; poiché, dopo il giro, le consonanze e le dissonanze si fanno per addizione e sottrazione degli stessi battimenti.
In effetti, finché non si aggiungerà niente, e non si toglierà niente a ciascuno dei due suoni, che, si suppongono produrre ognuno 8 battimenti, è certo che conservano sempre la stessa uguaglianza, andranno sempre a pari, e formeranno tra loro ciò che si chiama l'unisono.
Se al contrario a uno degli unisoni si aggiunge un secondo battimento, tanto che l'altro unisono sia fermo e allo stesso tono, si avranno 2 battimenti d'aria contro uno, e la proporzione di 2 a 1; due battimenti per il do acuto, e uno per il do grave.
E se si aumentano questi due battimenti di ottava di una terza, si avrà per la quinta tre battimenti al posto di due, perché la quinta è composta di due movimenti in ragione di 5 suoni, di cui uno batte l'aria due volte mentre l'altro lo batte tre volte.
Dove non arriva che una corda che sarà divisa in questo modo, tale che lascerà tre parti da un lato e due dall'altro, si avrà necessariamente la quinta, perché il lato che ha tre parti batterà 2 volte l'aria, mentre questo - che non ne ha che 2 - lo batterà 3 volte, essendo reciproco il numero dei battimenti rispetto alla lunghezza della corda.
Consiste nel mescolamento di due suoni, di cui la proporzione è 4 a 3; perché nello stesso tempo in cui la quarta acuta batte 4 volte l'aria, la sua tonica, cioè la quarta grave, non la batte che tre volte; è per questo che bisogna che la più grande campana di quarta grave sia più alta e più larga di un terzo dell'altra.
Affinché le altre consonanze si formino attraverso due movimenti, di cui uno batte l'aria 5 volte nella terza maggiore acuta, e l'altra quattro volte nella terza grave; sei volte per la terza minore acuta e 5 volte per la terza grave; ora, se dopo aver aggiunto tutti questi differenti battimenti d'aria per salire di tono in tono, li si smorza, si discenderà come si è saliti, di consonanza in consonanza, fino al primo suono.
Si manterrà ugualmente la stessa strada nelle dissonante, sia salendo che scendendo.
Se si suppongono i due unisoni composti di 8 battimenti d'aria ciascuno, si aggiunge a uno dei due un nono battimento, si avrà ciò che si chiama il tono o la seconda maggiore di 8 a 9, e aggiungendone ancora un secondo, si avrà ciò che si chiama il semitono o la seconda minore di 10 a 9; ma se dopo questa somma si volesse togliere un'unità, da 10 a 9, semitono diverrà tono.
Si forma anche con 3 battimenti d'aria, i quali aggiunti ai 5 battimenti della quinta, ne danno 8, e nello stesso tempo la proporzione di 8 a 5.
Non bisogna dimenticare il più grande termine, ossia la più alta cifra delle ottave che precedono di tono in tono, e ciò ripetute tante volte quanto si vorrà.
Il più grande termine di do grave della prima ottava è 2, che essendo raddoppiato dà 4 per il do grave della seconda ottava; ciò che si farà sicuramente quando si sarà osservato che, di ottava in ottava, i battimenti diminuiscono successivamente di metà, tanto che al contrario il volume delle campane aumenta del doppio in spessore, altezza, peso e larghezza, di misura che esse diminuiscono per ottava: è la proporzione inversa.
Portale "Ingegneria e
Campanologia" -
Autore -
Sommario
- Mappa del Sito -
Home
Bib-ST-000 - Testo di Ing. Arch. Michele Cuzzoni
Bib-ST-186 - Enciclopedia di Didérot - D'Alembert: traduzione a cura di Ing. Arch. Michele Cuzzoni
Bib-ST-187 - Disegni grafici tratti dalle Tavole grafiche (planches - Enciclopedia di Didérot - D'Alembert) presentate e spiegate in opportune pagine (vedi sommario)
Bib-ST-188 - Nota sulle tavole grafiche: documentazione desunta da: http://www.storiadelleimmagini.it/2010/09/disegno-incisioni-planches-goussier-encyclopedie/ (collegamento attivo fino al 2012)