Portale "Ingegneria e Campanologia" - Autore - Sommario - Mappa del Sito - Home
Suono e tono della Campana individuale
AREA I - ARTE TECNICO-SCIENTIFICA (ATS)
Cap. ATS-J02 - Acustica della Campana - Pag. ATS-J02.09
Gli argomenti trattati sono stati inseriti da Ing. Arch. Michele Cuzzoni nel 2012 - © Copyright 2007- 2024 - e sono desunti dalla documentazione indicata in Bibliografia a fondo pagina
Il disegno della Campana
Sulla progettazione di una campana è sempre prevalso in passato un equivoco popolare.
Spesso si assume che il profilo di una campana sia realizzato esclusivamente mediante un calcolo. Sarebbe quindi sufficiente avere nota la forma geometrica per conoscere la posizione dei parziali e quindi bastevole conoscere alcune teorie fisiche per calcolare il profilo.
Ma già dagli anni ’80 del secolo scorso, è vero il contrario.
Poiché solo da allora, grazie al computer, è stato possibile realizzare una rivoluzione nel progettare la campana.
Per ora, comunque, faremo l’approccio tradizionale, poiché la conoscenza del metodo specifico è indispensabile solo a un computer per progettare una campana.
In precedenza la metodologia di costruzione era così empirica, che il progetto era stato creato per aiutare. Per fortuna si aveva una ricca esperienza. Per ciò si aveva una inesauribile ricchezza di campane buone, e naturalmente, anche meno buone. Sarebbe pertanto sufficiente produrre una splendida campana con la stessa cura con cui se ne fanno copie. Ma questo è fin troppo semplice, perché ogni produzione ha un suo profilo distinto dai precedenti. Ma questo che senso ha? La risposta sembra essere negativa, perché quando si confrontano i profili dei fonditori contemporanei, evitano di farlo tra loro, anche se non sono inglesi. Le differenze di timbro sembrano determinate da altri fattori, ad esempio la qualità dei getti. Eppure, ci chiediamo quali siano le regole empiriche di produzione per aiutare a mantenere costante la forma di una campana scevra da piccole variazioni. Si deve concordare tuttavia in anticipo quali requisiti minimi debba avere una campana, e quelli storici sono aumentati senza i quali la campana non sarebbe una buona campana.
La campana
deve suonare piacevolmente, cioè i toni parziali della campana devono essere
ragionevoli e non dirompenti, di elevata purezza e taglienti. Per quanto
riguarda l’ultimo aspetto, il tipo di bronzo e la qualità dei getti hanno un
ruolo importante. Si veda a
![]() pag. J02.15 "Le
campane di bronzo o d'acciaio".
pag. J02.15 "Le
campane di bronzo o d'acciaio".
Ma il modello può avere un’influenza decisiva. Vale a dire che si può facilmente vedere che una piccola campana si può ottenere come un elemento a piastra. Al contrario, non si può escludere il rischio che una campana troppo spessa sia melodiosa e possedere tuttavia timbro tagliente.
Apparentemente vi è una relazione tra la forza dei parziali e lo spessore della parete. Ma non è così.
In
passato, è stato determinato che una campana troppo spessa, specialmente per
ottenere una campana ideale, come definito a pagina
![]() j02.01 "La nota della campana e le sue
sfumature", può difficilmente essere realizzata o per
nulla. Solo l’effetto di una parete leggermente più spessa o più sottile
può modificare il processo di assorbimento dei parziali nella struttura
armonica. Nei casi più estremi è impensabile. Quando abbiamo convertito tutto
ciò in numeri concreti, significa per esempio che una campana con un diametro di
77 cm, può essere sia un sib3 (parete sottile) oppure un re4 (parete spessa).
L’ideale si trova come do4. Questo è determinato dal
principio di simulazione dinamica (Cfr.
j02.01 "La nota della campana e le sue
sfumature", può difficilmente essere realizzata o per
nulla. Solo l’effetto di una parete leggermente più spessa o più sottile
può modificare il processo di assorbimento dei parziali nella struttura
armonica. Nei casi più estremi è impensabile. Quando abbiamo convertito tutto
ciò in numeri concreti, significa per esempio che una campana con un diametro di
77 cm, può essere sia un sib3 (parete sottile) oppure un re4 (parete spessa).
L’ideale si trova come do4. Questo è determinato dal
principio di simulazione dinamica (Cfr.
![]() pag. J04.01 "Il
Principio di Simulazione Dinamica"). Tutto questo vale per le campane non troppo piccole. Per
quelle acute sono diverse le regole applicate (Cfr.
pag. J04.01 "Il
Principio di Simulazione Dinamica"). Tutto questo vale per le campane non troppo piccole. Per
quelle acute sono diverse le regole applicate (Cfr.
![]() pag. K01.02
"Dimensionamento delle Campane da Carillon").
pag. K01.02
"Dimensionamento delle Campane da Carillon").
Il modello base è quindi chiaro. E’ stato derivato da esempi di torri in cui è noto l’accordo delle campane realizzate, oppure ancora che può essere realizzato. Questo accordo, e lo ripetiamo ancora una volta, deve possedere almeno la seguente immagine (esempio, campana do4):
|
Parziale |
Tipo |
Nota corrispondente |
|
Subbasso |
I-2 |
Do3 |
|
Prima |
II-2 |
Do4 |
|
Terza Minore |
I-3 |
Mib4 |
|
Quinta |
II-3 |
Sol4 |
|
Ottava |
I-4 |
Do5 |
In questa presentazione abbiamo ancora ignorato la questione se si debba dare un’accordatura ai parziali di una campana con temperamento moderno equabile oppure un’accordatura storica.
Ora si deve solo notare che si tratta di visualizzare una campana per attribuirle un tono inequivocabile.
Si devono principalmente considerare il Subbasso, la Prima e l’Ottava, dopo il tono di battuta do4, mentre la terza minore mib4, e la quinta sol4 sono le armoniche aggiunte che danno colore al suono.
Naturalmente, questo non implica che le armoniche più alte debbano essere tralasciate.
Un problema interessante è, ad esempio la questione di come debba essere il rapporto di duodecima I-5 rispetto alla doppia ottava I-6 e all’ottava I-4, quindi come variano i rapporti rispetto al tono di battuta primario. Dovrebbe allora essere chiaro che questo problema coinvolge anche la terza minore I-3.
Dopo tutto, i toni dello stesso gruppo lavorano insieme quasi sempre. In un gruppo un intervallo può essere sempre allargato, quindi seguiranno altre parziali. Se applichiamo questo concetto al primo gruppo, si può anzitutto osservare che la seguente serie da I-3 a I-6 si realizza bene ed è la più comune:
mib4 – do5 – sol5 – do6+
Se così fosse, tuttavia, la doppia ottava ha solo bisogno di presenziare, mentre non ci sarebbe rispetto all’ottava I-4 come nel seguente esempio:
mib4 + – do5 – sol5- – do6
Ciò va a scapito della terza e della dodicesima.
E’, quindi, solo con i cambiamenti estremi del profilo che questi quattro armonici puri possono essere presenti.
Un altro problema è l’insieme della terza maggiore mi4 (II-4), della prima undicesima fa5- (III-2) e della seconda undicesima fa5+ (III-3). Questi parziali sono troppo vicini tra loro, se compaiono durante il transitorio d’attacco e poco dopo durante il suono pieno si verificano effetti molto spiacevoli.
Pertanto sembra solo un’opzione ridurre la terza maggiore mi4 alla terza minore mib4, e questo è tanto maggiore perché la terza minore mib4 crea un rapporto con il parziale di ottava. Può servire a verificare progressivamente quali siano le conseguenze di questo intervento in altre parti del suono.
Un esempio: se si ha la terza maggiore bassa, allora troppo spesso saranno tutti associati con una quinta bassa.
Con tutto ciò si apprezzerà che nella progettazione di una campana non è un problema quello di avvicinarsi il più precisamente possibile alla tonalità di una campana ideale, bensì presumere che questa obiezione si possa trasmettere alla campana da fare.
Al contrario, la progettazione di una campana composta dalle componenti più favorevoli comporta di far uso di caratteristiche spesso contrastanti in modo che si ottenga il miglior compromesso.
Quindi si ha una visione personale di tale compromesso quando si vogliono creare campane che hanno una colata proprio ideale.
Al fine di progettare una campana così, si deve possedere una buona conoscenza delle conseguenze dei cambiamenti di modello. La fusione deve quindi sapere quale sarà l’effetto sulla posizione dei parziali quando si effettua una particolare modifica per creare il profilo.
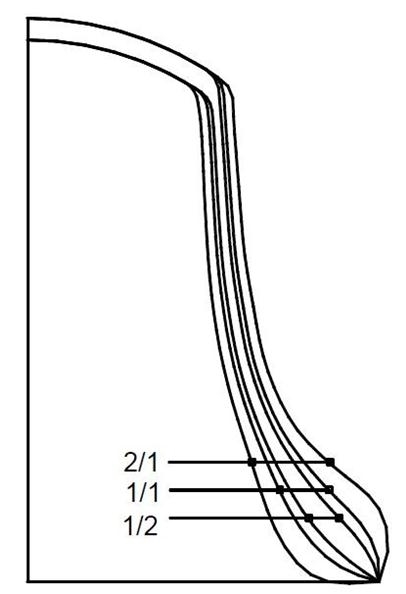
In figura 01 è dato l’esempio più semplice. Tre campane di prova con spessore ½ del normale e 2/1. Nello spessore normale le loro frequenze sono state attentamente misurate.
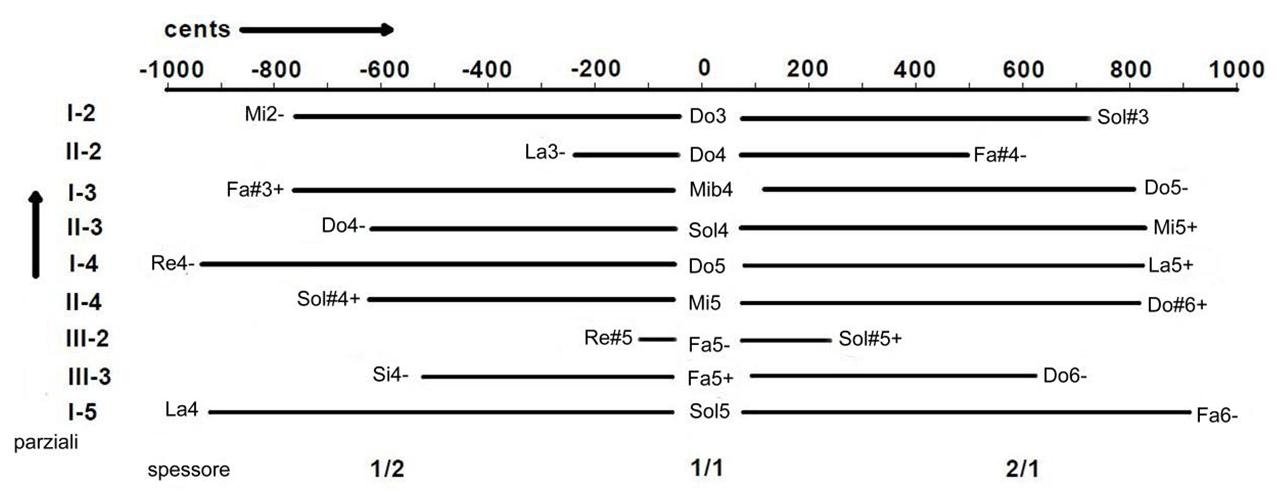
Figura 01: Assottigliamento e ispessimento.
|
Figura 02: Spostamento delle parziali nello spessore di 1/2 - 1/1 - 2/1 |
La figura 02 a sinistra, mostra il risultato in forma schematica. Vi è la campana con spessore normale, in modo che si legga il solito suono complessivo. Questo stato è leggibile dall’alto verso il basso al centro della tabella (Fig. 01). A sinistra si può vedere l’effetto di una parete sottile fino a ½ del suo valore originale. Questo comporta di specificare la lunghezza della linea orizzontale per diminuire il tono. La riga superiore si può leggere in centesimi. La cosa più sorprendente è che la campana viene completamente sconvolta. Le cinque parziali che partecipano per metà dello spessore sono più basse, e considerando il valore di ottava si è fissato il do5 e vale la seguente relazione: re3- sol4- mi4+ sib4- do5 Ciò fa di una campana uno strumento inutilizzabile. Qualcosa di simile, come si vede nella figura, si applica anche per un bordo ispessito fino a due volte il suo valore originale. La causa sta nel fatto che le parziali reagiscono ciascuna a modo loro a seconda che si assottigli o si ispessisca il bordo. Naturalmente, in pratica, non si impiegheranno tali variazioni all’estremo. Ma attraverso qualche interpolazione si sarà in grado di visualizzare la fusione e di stabilire gli effetti dei piccoli cambiamenti necessari per realizzare lo spessore ottimale che permetterà di effettuare certi cambiamenti nello spettro sonoro. Tuttavia non ci si può fermare alla conoscenza di una sola variazione di profilo, al contrario, occorre progettare più campane da mettere a disposizione dello studio, alcuni esempi dei quali sono visualizzati in figura 03 a sinistra. |
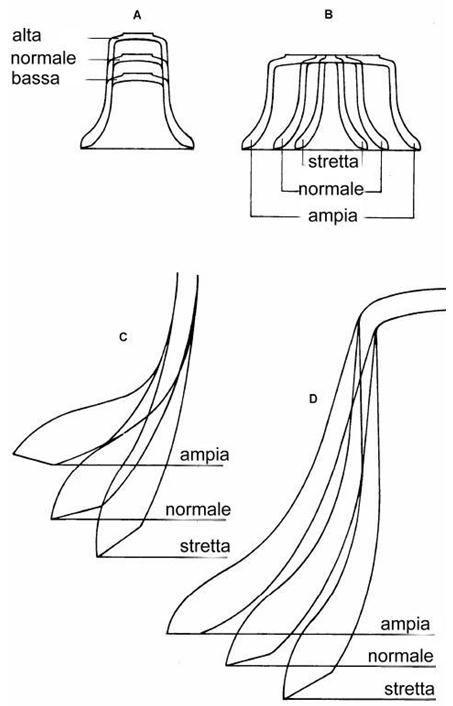 Figura 03: Variazioni del profilo. |
In A c’è solo la variazione di altezza. In B modifiche nel diametro. In C l’anello di battuta piegato verso l’esterno o l’interno. Mentre in D le modifiche sono fatte per l’intero bordo. Le maggiori variazioni fatte comportano di gran lunga un cambio di modello, per cui più frequentemente si usano variazioni locali di spessore della parete. Il risultato che si ottiene per l’ubicazione del parziale, consente di leggere in un grafico con precisione quel è la conseguenza di un assottigliamento o ispessimento della parete locale. Per tanto le modifiche di fusione molto sottili incidono nello spettro sonoro di una campana; l’importanza di questo tipo di grafici risulta anche dal fatto che essi sono in sintonia con l’uso delle campane. Si veda questo aspetto a
Resta da parlare dei computer di cui hanno fatto uso alcune fonderie di campane. Ci sono due modi per cui si può usare il disegno del computer. 1). Il primo è che un particolare profilo può essere calcolato velocemente. In precedenza quando si progettava una campana era necessario calcolare uno o più campioni, ora grazie al computer questo non è più necessario. 2). La seconda applicazione è che il computer può specificare che struttura tonale deve avere un nuovo tipo di campana, dopo di che calcola gli elementi che appartengono a questo profilo. Si comincia con la prima applicazione. Per il calcolo delle frequenze naturali, le parziali primitive, si ricorre all’uso di programmi informatici che si basano sul metodo degli elementi finiti. Tali programmi hanno molte applicazioni in ingegneria. Possono essere classificati in due gruppi principali . Nel primo gruppo il programma calcola la forza di una costruzione, per esempio di un ponte, di una gru, ma eventualmente anche di una campana. Nel secondo gruppo ci sono le frequenze naturali di una struttura centrale, per esempio di un ponte, di una torre, ma anche della campana che vibra. |
|
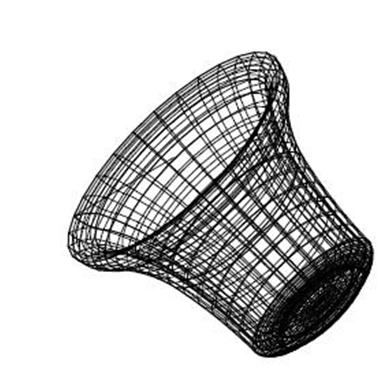
Figura 04: Suddivisione a elementi finiti di una campana. |
Il metodo qui è il seguente. Innanzitutto l’oggetto da esaminare è diviso in un gran numero di piccoli cubi virtuali, detti elementi. Per una campana, il numero è dell’ordine di grandezza di almeno 1000. La figura 04 mostra una campana divisa in tali elementi. La campana è inclinata per rendere più visibili gli elementi. Poi per ciascun elemento si formulano un certo numero di equazioni algebriche, che segnalano la deformazione dell’elemento per effetto di una forza esterna, o per l’effetto delle vibrazioni. Dopo di ciò tutti gli elementi sono considerati come un oggetto in modo che se ne possa misurare l’energia cinetica durante la vibrazione della campana e l’energia potenziale a riposo. Nell’ultimo passaggio le frequenze naturali vengono calcolate in questo modo. Il ruolo del computer in questo processo è la capacità di compiere migliaia di operazioni che sarebbero impossibili da risolvere manualmente. Tuttavia per un computer, il calcolo di una campana è una questione di secondi. Sarà chiaro che il grande vantaggio consiste nel comprendere rapidamente gli effetti acustici di un dato profilo. Eppure sono richieste le regole tradizionali di disegno: il fonditore di campane deve sapere come deve cambiare il suo modello di campana per raggiungere l’obiettivo desiderato. |
In breve, in questo metodo, il computer è un grande strumento, ma non disegna ancora nessuna campana. Si calcolano solo le forme parziali di un profilo che il programma può accettare.
La diversità appare nella seconda applicazione. In tal caso non solo si deve tener conto del metodo degli elementi finiti, per il calcolo delle parziali naturali di un profilo, ma in aggiunta si usa un programma di ottimizzazione che cerca un profilo ottimale per lo scopo desiderato. Il fonditore di campane fornisce al programma un profilo di base più o meno arbitrario e l’obiettivo per le cinque parziali più basse, come la terza maggiore di una campana, come mostrato dal seguente schema:
do3 do4 mi4 sol4 do5
La procedura è la seguente:
Innanzitutto il programma degli elementi finiti calcola le frequenze del profilo di base. In generale queste non corrispondono ancora allo scopo perseguito. Per questo motivo, il profilo viene raffinato usando un programma di ottimizzazione guidato da una certa metodologia matematica che può apportare cambiamenti nel profilo.
Questo profilo è calcolato con il sistema delle autofrequenze. L’esperienza dimostra che l’obiettivo non è ancora raggiunto, anche se si è fatto un passo avanti. Per questo motivo, occorre cambiare di nuovo qualcosa del profilo nell’ottimizzatore, si calcola poi con le frequenze, ecc.
Passo dopo passo, dunque, l’obiettivo è raggiunto, almeno se questo obiettivo fosse possibile in realtà. Perché questo non è sempre verificato. Il metodo qui descritto è noto come processo iterativo. Ogni ottimizzazione del profilo è una iterazione di calcolo. Al fine di raggiungere l’obiettivo, si compiono centinaia di iterazioni. L’accordatura di una campana è un processo iterativo, fatto a piccoli passi controllati che portano a questo obiettivo.
Portale "Ingegneria e
Campanologia" -
Autore -
Sommario
- Mappa del Sito -
Home
Bib-TS-000 - Testo di Ing. Arch. Michele Cuzzoni
Bib-TS-246 - André Lehr - Een klankanalyse van de 16de-eeuwse Van Wou-klokken in de Domtoren te Utrecht (Asten, 1980)
Bib-TS-247 - André Lehr - Partial Groups in the Bell Sound. In: The Journal of the Acoustical Society of America , vol.79, 1986, blz.2000-2011
Bib-TS-248 - André Lehr - The designing of swinging bells and carillon bells in the past and present (Asten, 1987)
Bib-TS-249 - André Lehr - The tuning of the Bells of Marquis Yi. In: Acustica , vol.67, 1988, blz.144-148
Bib-TS-250 - André Lehr - A statistical investigation of historical swinging bells in West Europe. In: Acustica , vol.74, 1991, blz.97-108
Bib-TS-251 - André Lehr - Profielconstructies van luid- en beiaardklokken in het verleden (Asten, 1991)
Bib-TS-252 - André Lehr - Acoustic research. In: 45 Years of Dutch Carillons 1945-1990 , L.Boogert, A.Lehr, J.Maassen (ed.), 1992, blz.132-145
Bib-TS-253 - André Lehr - Vormoptimalisatie van luid- en beiaardklokken. In: Symposium Structural Optimization in the Netherlands , F. van Keulen en A.J.G. Schoofs (ed.), November 9, 1995, Technische Universiteit Delft
Bib-TS-254 - André Lehr - Berekening van het klokprofiel. De eindige-elementen-methode in combinatie met optimalisatie-techniek helpt een oud ambacht. In: Principieel, werktuigbouwkundig magazine, Universiteit Twente , jg.1, Lente 1997, blz.23-28
Bib-TS-255 - André Lehr - Designing Chimes and Carillons in History. In: Acustica, 1997, vol.83, blz.320-336
Bib-TS-256 - André Lehr - Metaalkunde en Torenklokken. In: Metalen in Monumenten en Vernieuwbouw , Syllabus van de Studiedag van WTA, Nederland-Vlaanderen, Wetenschappelijk-Technische Groep voor Aanbevelingen inzake Bouwrenovatie en Monumentenzorg, op 21 november 1997 in het Provinciehuis te Antwerpen, blz.60-73
Bib-TS-257 - André Lehr - Campanologie. Een leerboek over klank en toon van klokken en beiaarden (Mechelen, 1997, 2de druk 1998)
Bib-TS-258 - André Lehr - The Geometrical Limits of the Carillon Bell. In: Acustica, vol.86, 2000, blz.543-549
Bib-TS-259 - André Lehr - The Removal of Warbles or Beats in the Sound of a Bell. In: Acustica , vol.86, 2000, blz.550-556
Bib-TS-260 - André Lehr - Geschiedenis van de campanologie (Asten, 2001)
Bib-TS-261 - André Lehr - Leerboek der Campanologie, 2007