Portale "Ingegneria e Campanologia" - Autore - Sommario - Mappa del Sito - Home
Campane da Carillon
AREA I - ARTE TECNICO-SCIENTIFICA (ATS)
Cap. ATS-K01 - Carillon - Pag. ATS-K01.02
Gli argomenti trattati sono stati inseriti da Ing. Arch. Michele Cuzzoni nel 2012 - © Copyright 2007- 2024 - e sono desunti dalla documentazione indicata in Bibliografia a fondo pagina
A
![]() pag. J04.01 "Il
Principio di Simulazione Dinamica", mediante il
principio della somiglianza dinamica, si era sviluppato un
metodo per calcolare e controllare le dimensioni delle
campane oscillanti. La tabella delle campane presentata in quella pagina
è stato il risultato di quei calcoli.
pag. J04.01 "Il
Principio di Simulazione Dinamica", mediante il
principio della somiglianza dinamica, si era sviluppato un
metodo per calcolare e controllare le dimensioni delle
campane oscillanti. La tabella delle campane presentata in quella pagina
è stato il risultato di quei calcoli.
La questione ora è se questo metodo possa essere applicato anche ai carillon.
O, ancora più specificamente, come si possono trasferire le dimensioni e i pesi di quelle campane ai carillon?
Come si
può leggere a
![]() pag. K01.04 "Come si
deve intonare precisamente un carillon", le campane di un carillon sono leggermente
diverse. Ogni tipo di campana da carillon ha quindi
un proprio profilo. Esso ha a che fare con la posizione del parziale di terza
minore. D’altra parte è chiaro che ci sono differenze molto sottili sia
in sezione trasversale sia in peso.
pag. K01.04 "Come si
deve intonare precisamente un carillon", le campane di un carillon sono leggermente
diverse. Ogni tipo di campana da carillon ha quindi
un proprio profilo. Esso ha a che fare con la posizione del parziale di terza
minore. D’altra parte è chiaro che ci sono differenze molto sottili sia
in sezione trasversale sia in peso.
Da questo punto di vista, le campane da oscillazione sono quasi identiche alle campane da carillon, ma con la condizione che le campane da carillon, nella maggior parte dei casi, sono senza corona. I pesi calcolati con la corona, in questo contesto, hanno poco significato.
Tuttavia le campane da carillon ad alto volume hanno la corona sono all’inizio delle due ottave.
Ai fini del carillon che si può estendere oltre il do8, questa tabella dovrebbe essere prolungata negli acuti.
Con l’aiuto del principio della somiglianza dinamica si calcola, per esempio, che una campana do7 ha un diametro di 97 mm con un peso di circa ½ kg. Il do8 avrebbe un diametro di soli 49 mm e un peso di non più di 65 grammi.
|
Figura 01: due campane do7 (diametro 97 e 194 mm) |
Va da se’ che queste relazioni sono più pratiche per le campane pesanti. Le campane più acute diventano quasi impercettibili. Per risolvere questo problema, ma è solo un mezzo a disposizione, si usano i campanelli di sagoma pesante. Più sono pesanti e avranno il tono più potente. Si sa che una campana con lo stesso tono può avere una parete più spessa. Se si vuole mantenere la tonalità, pertanto, non solo la parete sarà più spessa, ma anche il diametro sarà più grande. Il seguente esempio può chiarire il concetto con i numeri arrotondati. Un do7, secondo i calcoli di cui sopra, ha un diametro di 97 mm e un peso di ½ kg. Se si raddoppia lo spessore della parete, il peso aumenta a 1 kg, mentre la tonalità aumenta complessivamente di un’ottava. Infatti un raddoppio dello spessore della parete corrisponde approssimativamente a un rapporto di frequenza 2/1. Il tono è così do8. Per poter tornare nuovamente a do7, si può usare il principio della somiglianza dinamica. La campana è due volte più grande in tutte le dimensioni, per cui il diametro è 194 mm e il peso è 8 x 1 = 8 kg. Il risultato si può vedere in figura 01 a sinistra. A un do7 piccolo corrisponde un do7 relativamente grande con parete più spessa. |
La conclusione da quanto precede è evidente. Quando il gioco di campane è più acuto, occorre ingrandire le dimensioni delle campane e quindi si applica il principio di similitudine dinamica.
Ciò è illustrato in figura 02 sottostante: sull’asse orizzontale ci sono i toni delle campane, sull’asse verticale i diametri in mm. La linea delle campane da oscillazione arriva al massimo a do7, con l’annotazione ovvia da fare che campane forti più acute non esistono.

Figura 02: Pesi di campane da carillon da do4 leggere e pesanti
Asse x = note - Asse y = mm
Un tono di mi5 è il massimo. Le altre due linee indicano dimensioni possibili per un gioco di campane.
Una prima conclusione è che fino al re4 le dimensioni di campane da carillon sono uguali a quelle delle campane da oscillazione. Solo dopo quella nota si potranno avere campane proporzionalmente più grandi e quindi più pesanti.
La pratica ha così portato a due tipi di peso, mentre le campane da carillon relativamente leggere si avevano in carillon che si basano principalmente su esempi storici particolarmente pesanti che si producevano negli anni ’50 e ’60 del secolo XX.
Si noti tuttavia che tali linee non sono state calcolate, ma si sono ottenute da una libera scelta sulla base dell’esperienza.
Da qui due possibilità diverse.
Considerando la dimensione dei carillon, in piccole torri basse servono soprattutto campane piccole e leggere, mentre si applicano campane pesanti per carillon estesi in torri alte. Questi pesi sono visibili in figura 03 sottostante.

Figura 03: Pesi di campane da carillon da do4 leggere e pesanti
Asse x = nota fondamentale – Asse y = kg – Asse y = mm
Nella tabella 01 sottostante la formula per trovare i pesi delle campane da carillon con i valori più accurati dei diametri elencati, valori che sono di uso comune.
Inoltre, ogni volta il peso è dato senza la corona.Sono valori ricavati sulla base di una formula che non viene ulteriormente illustrata. Vi si legge:
M = c . f . D4
Dove:
m = peso in kg senza corona
f = frequenza del tono fondamentale (subbasso)
D = diametro in metri
c = costante che dipende dal profilo utilizzato
Per esempio, nei calcoli presenti, c = 2,8 kg . sec / m4
Una campana la3 (sagoma media) con una frequenza fondamentale di 220 Hz e un diametro di 0,925 metri pesa: 2,8 . 220 . 0,9254 = 451 kg
In questo contesto è possibile stabilire una statistica correlata, ossia il cosiddetto valore f D, cioè il prodotto della frequenza del tono fondamentale per il diametro in metri.
Per esempio per impostare una campana la3, si ha: f D = 220 . 0,925 = 203,5 m/s.
Il valore f D dice qualcosa circa lo spessore della parete di una campana.
Una campana la5, secondo un certo profilo, ha un f D = 880 . 0,231 = 203 m/s, ossia lo stesso valore arrotondato del precedente.
Ciò era ovvio anche perché queste sono campane che possono essere create secondo il principio della somiglianza dinamica. Ad esempio, la frequenza è raddoppiata mentre il diametro è dimezzato, cosicché il valore f D non cambia.
Tuttavia, supponiamo di voler considerare una campana la5 con un diametro di 276 mm in base al profilo pesante, quindi con parete spessa. f D = 880 x 0,276 = 242,9 m/s.
Apparentemente il valore f D è una misura dello spessore della parete di una campana. Per i profili pesanti di carillon la campana do8 può arrivare fino a 0,750 m/s, per i profili leggeri fino a oltre 600 m/s.
|
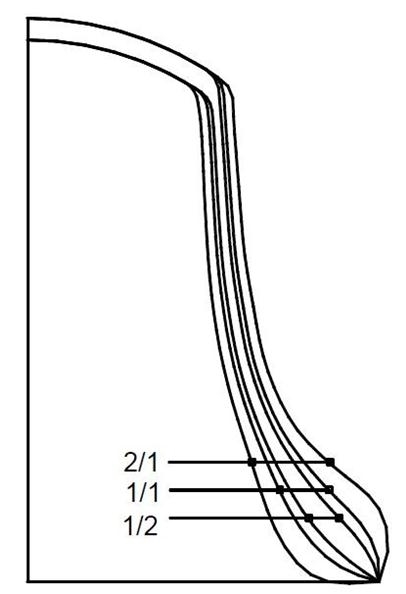
Figura 04: Spostamento delle parziali nello spessore di 1/2 - 1/1 - 2/1 |
Dalla
Nei giochi di campane, però, si è agito in modo diverso. Nell’esempio precedentemente menzionato, una campana do7 ha un profilo pesante con un diametro di 216 mm. Se la campana fosse una campana normale, con questa sezione si avrebbe un sib5, quindi con una differenza di più di un’ottava. Questo è comunque accettabile per le campane piccole, sulla base delle seguenti considerazioni. Come
è stato dichiarato a
Certo, con alcune modifiche locali si può ottenere un profilo quasi ideale, ma mai completamente. Nella
figura 02 di
Nelle campane soprane di un carillon si sarebbero sentiti i primi parziali troppo bassi. Fortunatamente, però, il parziale di Prima troppo basso è compensato dall’altezza ridotta della campana. Giochi di campane piccoli non sono solo più spessi del normale, ma anche inferiori di parziali. E’ anche possibile, ovviamente avere la testa della campana spessa, in modo che l’altezza interna sia ridotta, senza che ciò sia visibile all’esterno. Lo svantaggio di una testa grande, tuttavia, è che la campana suona frenata. |
Per quanto riguarda la Prima è possibile intervenire, tuttavia, in misura molto minore per le altre parziali.
Il tono di Quinta, per effetto dell’ispessimento delle pareti e per la riduzione delle pareti, rimane sempre alta, mentre le parziali al di sopra dell’ottava I-4 hanno altri problemi. Tutto questo, tuttavia, non è discutibile. Poiché si tratta di campane acute, il sistema uditivo è meno sensibile ai bassi. Quindi nelle campane acute le armoniche superiori possono essere leggermente diverse, mentre la quinta armonica, che ha un nodo nell’anello di battuta, non è più sentita. Le campane più piccole hanno la quinta spesso associata alla terza minore, mentre l’ottava più alta non è nemmeno da prendere in considerazione. Ma ci sono obiezioni per cui il tono più alto è meno valido. Quindi giochi di campane a 5 ottave possono avere molti difetti!
Per quanto riguarda l’intonazione interna al gioco di campane acute, esistono poche obiezioni riguardo l’ispessimento relativo della parete. Questo sembra meno favorevole per i tempi di suono. Sembra che più la parete è spessa e più breve è il tempo di suono. Fortunatamente questo fatto viene compensato dal fatto che una parete più spessa nella campana, a sua volta riceve un più lungo tempo di smorzamento.
Oppure, per fare un esempio, ogni campana do7 suona circa 10 secondi, indipendentemente dalle sue dimensioni. Ma, va notato ancora una volta per essere sicuri, queste campane devono essere delle buone campane con alto contenuto di stagno e fusione d’eccezione.
|
Nota fondamentale |
Profilo leggero |
Profilo pesante |
||
|
Diametro (mm) |
Peso senza corona (kg) |
Diametro (mm) |
Peso senza corona (kg) |
|
|
Dimensioni e pesi per campane da carillon a partire dal do4 per lo stesso carillon.
Vedere
|
||||
|
Do4 |
778 |
268 |
778 |
268 |
|
Do#4 |
734 |
225 |
735 |
226 |
|
Re4 |
693 |
190 |
697 |
194 |
|
Re#4 |
655 |
160 |
662 |
167 |
|
Mi4 |
621 |
137 |
629 |
144 |
|
Fa4 |
589 |
118 |
599 |
126 |
|
Fa#4 |
559 |
101 |
570 |
109 |
|
Sol4 |
530 |
87 |
544 |
96 |
|
Sol#4 |
503 |
74 |
519 |
84 |
|
La4 |
478 |
64 |
495 |
74 |
|
La#4 |
455 |
56 |
474 |
66 |
|
Si4 |
432 |
48 |
453 |
58 |
|
Do5 |
412 |
42 |
434 |
52 |
|
Do#5 |
392 |
37 |
417 |
47 |
|
Re5 |
374 |
32 |
400 |
42 |
|
Re#5 |
357 |
28 |
385 |
38 |
|
Mi5 |
341 |
25 |
370 |
35 |
|
Fa5 |
326 |
22 |
357 |
32 |
|
Fa#5 |
312 |
20 |
435 |
29 |
|
Sol5 |
299 |
17 ½ |
333 |
27 |
|
Sol#5 |
287 |
16 |
322 |
25 |
|
La5 |
276 |
14 ½ |
312 |
23 |
|
La#5 |
265 |
13 |
303 |
22 |
|
Si5 |
255 |
11 ½ |
294 |
21 |
|
Do6 |
246 |
10 ½ |
286 |
20 |
|
Do#6 |
238 |
10 |
278 |
18 ½ |
|
Re6 |
230 |
9 |
270 |
17 ½ |
|
Re#6 |
222 |
8 ½ |
264 |
17 |
|
Mi6 |
215 |
8 |
257 |
16 |
|
Fa6 |
209 |
7 ½ |
251 |
15 ½ |
|
Fa#6 |
203 |
7 |
245 |
15 |
|
Sol6 |
197 |
6 ½ |
240 |
14 ½ |
|
Sol#6 |
192 |
6 |
234 |
14 |
|
La6 |
187 |
5 ½ |
229 |
13 ½ |
|
La#6 |
182 |
5 ½ |
225 |
13 ½ |
|
Si6 |
178 |
5 ½ |
220 |
13 |
|
Do7 |
175 |
5 |
216 |
13 |
|
Do#7 |
171 |
5 |
212 |
12 ½ |
|
Re7 |
168 |
5 |
208 |
12 ½ |
|
Re#7 |
165 |
5 |
204 |
12 |
|
Mi7 |
162 |
5 |
201 |
12 |
|
Fa7 |
160 |
5 |
197 |
12 |
|
Fa#7 |
158 |
5 |
194 |
11 ½ |
|
Sol7 |
156 |
5 |
191 |
11 ½ |
|
Sol#7 |
155 |
5 ½ |
189 |
12 |
|
La7 |
154 |
5 ½ |
186 |
12 |
|
La#7 |
153 |
5 ½ |
184 |
12 |
|
Si7 |
153 |
6 |
182 |
12 |
|
Do8 |
153 |
5 ½ |
180 |
12 ½ |
|
Dimensioni e pesi per campane da carillon |
||||
Portale "Ingegneria e
Campanologia" -
Autore -
Sommario
- Mappa del Sito -
Home
Bib-TS-000 - Testo di Ing. Arch. Michele Cuzzoni
Bib-TS-246 - André Lehr - Een klankanalyse van de 16de-eeuwse Van Wou-klokken in de Domtoren te Utrecht (Asten, 1980)
Bib-TS-247 - André Lehr - Partial Groups in the Bell Sound. In: The Journal of the Acoustical Society of America , vol.79, 1986, blz.2000-2011
Bib-TS-248 - André Lehr - The designing of swinging bells and carillon bells in the past and present (Asten, 1987)
Bib-TS-249 - André Lehr - The tuning of the Bells of Marquis Yi. In: Acustica , vol.67, 1988, blz.144-148
Bib-TS-250 - André Lehr - A statistical investigation of historical swinging bells in West Europe. In: Acustica , vol.74, 1991, blz.97-108
Bib-TS-251 - André Lehr - Profielconstructies van luid- en beiaardklokken in het verleden (Asten, 1991)
Bib-TS-252 - André Lehr - Acoustic research. In: 45 Years of Dutch Carillons 1945-1990 , L.Boogert, A.Lehr, J.Maassen (ed.), 1992, blz.132-145
Bib-TS-253 - André Lehr - Vormoptimalisatie van luid- en beiaardklokken. In: Symposium Structural Optimization in the Netherlands , F. van Keulen en A.J.G. Schoofs (ed.), November 9, 1995, Technische Universiteit Delft
Bib-TS-254 - André Lehr - Berekening van het klokprofiel. De eindige-elementen-methode in combinatie met optimalisatie-techniek helpt een oud ambacht. In: Principieel, werktuigbouwkundig magazine, Universiteit Twente , jg.1, Lente 1997, blz.23-28
Bib-TS-255 - André Lehr - Designing Chimes and Carillons in History. In: Acustica, 1997, vol.83, blz.320-336
Bib-TS-256 - André Lehr - Metaalkunde en Torenklokken. In: Metalen in Monumenten en Vernieuwbouw , Syllabus van de Studiedag van WTA, Nederland-Vlaanderen, Wetenschappelijk-Technische Groep voor Aanbevelingen inzake Bouwrenovatie en Monumentenzorg, op 21 november 1997 in het Provinciehuis te Antwerpen, blz.60-73
Bib-TS-257 - André Lehr - Campanologie. Een leerboek over klank en toon van klokken en beiaarden (Mechelen, 1997, 2de druk 1998)
Bib-TS-258 - André Lehr - The Geometrical Limits of the Carillon Bell. In: Acustica, vol.86, 2000, blz.543-549
Bib-TS-259 - André Lehr - The Removal of Warbles or Beats in the Sound of a Bell. In: Acustica , vol.86, 2000, blz.550-556
Bib-TS-260 - André Lehr - Geschiedenis van de campanologie (Asten, 2001)
Bib-TS-261 - André Lehr - Leerboek der Campanologie, 2007