INDICE:

• Riassunto della Pagina

• 01. Introduzione

• 02. Definizione del Problema

• 03. Contatto Hertziano: soluzione mediante il metodo delle WF

• 04. Analisi delle effettive condizioni di contatto

  • 4.1. Modellazione ad elementi finiti

  • 4.2 Calcolo dei FIS effettivi utilizzando il metodo delle WF

• 05. Conclusioni

INDICE

Molti componenti meccanici e strutturali ( es. ruote dentate, cuscinetti, ruote ferroviarie,…) vanno soggetti a danneggiamento per fatica superficiale. Nella fase di innesco e prima propagazione le fessure si presentano usualmente inclinate rispetto alla superficie [1,..,3]. In questi casi la condizione tipica di carico può essere rappresentata dalla distribuzione di pressioni dovuta al contatto elastico tra i corpi, in moto sulla superficie.

Questa passa periodicamente sulla bocca della fessura e ne può essere influenzata a causa della diversa cedevolezza del corpo in funzione della posizione del carico rispetto alla fessura stessa.

Un’analisi della vita a fatica del componente basata su un approccio di meccanica della frattura richiede lo studio del problema al variare della lunghezza della fessura.

La valutazione dei parametri di meccanica della frattura per questo tipo di cricche non è semplice, considerando che molto spesso per migliorare la resistenza a fatica vengono realizzati trattamenti superficiali che in genere introducono specifiche distribuzioni di tensioni residue nel pezzo [4] e conseguentemente il campo locale di tensioni può presentare notevoli gradienti attraverso lo spessore.

La presenza di lubrificante che può essere pompato nella fessura ed intrappolato durante il passaggio del cilindro rende il problema ancora più complesso da affrontare [5,6]. Inoltre l’analisi basata su un approccio di meccanica della frattura risulta complicata dalla mancanza di simmetria del problema che induce modo misto di frattura per qualsiasi condizione di carico applicata [7]. Infine le particolari condizioni di carico generano una condizione di parziale chiusura della fessura [8] rendendo la soluzione del problema non lineare.

In tal caso le forze scambiate tra le superfici di frattura che vengono in contatto influenzano sia la configurazione della fessura sia i valori finali dei fattori di intensificazione della tensioni [9] ragion per cui devono essere accuratamente valutate.

L’approccio basato sulle WF si è dimostrato particolarmente efficace per risolvere questo tipo di problema [10]. Nel caso della fessura obliqua è stata recentemente proposta una formulazione matriciale della WF, i cui termini sono espressi tramite una serie troncata di potenze [11]. Partendo da questa formulazione è stata anche determinata in forma analitica la GF [12] tramite la quale le componenti di COD possono essere determinate attraverso una integrazione diretta per qualsiasi condizione di carico applicata alle facce della fessura.

Partendo da questa formulazione è possibile usare la GF in una procedura iterativa che permette di risolvere la non linearità del problema legata alle condizioni di parziale chiusura della fessura [13]. Infatti, partendo da una condizione di chiusura di primo tentativo è possibile in modo molto efficiente, modificare passo passo l’estensione delle regioni di contatto finchè le condizioni di compatibilità fisica sono soddisfatte su tutta la fessura entro una certa tolleranza.

In questo lavoro, questo approccio è applicato allo studio del problema di contatto ciclico indotto dal movimento di un corpo cilindrico sulla superficie di un semipiano caratterizzato dalla presenza di una fessura di bordo obliqua. L'analisi si può applicare anche alle campane, nel caso di percussione con battaglio in posizione diversa dall'usuale punto di battuta e conseguente rotolamento del battaglio sul bordo della campana.

Particolare attenzione viene rivolta all’analisi dell’effetto della cedevolezza del corpo sulla distribuzione delle pressioni ed alla valutazione dell’effetto della stessa sui valori del FIS e di COD della fessura. Per lo studio delle condizioni di contatto vengono considerate sia l’ipotesi di distribuzione delle pressioni dedotta dalla trattazione di Hertz del problema, sia la distribuzione delle pressioni che scaturisce nell’ipotesi più realistica che tiene conto della diversa deformabilità del corpo.

Quest’ultima informazione si ricava per mezzo di un’accurata analisi ad elementi finiti che simula il passaggio del cilindro sulla bocca della fessura. Il problema della determinazione del FIS e del COD viene risolto utilizzando il metodo proposto, tenendo conto dell’influenza sui valori di K_I e K_II delle pressioni e delle azioni tangenziali di attrito che nascono nelle porzioni chiuse della fessura al variare delle condizioni di carico. L’analisi è stata condottaconsiderando differenti angoli di inclinazione della fessura, differenti dimensioni della zona di contatto rispetto alle dimensioni della fessura e differenti condizioni di attrito tra le facce della fessura in contatto.

Una schematizzazione del problema è riportata in figura 1 e presenta un semipiano che contiene una fessura obliqua di lunghezza a inclinata di un angolo θ rispetto alla normale alla superficie.

Un cilindro di raggio R si muove sulla superficie del semipiano. La coordinata L rappresenta la posizione istantanea rispetto alla bocca della fessura. La forza per unità di spessore W rappresenta la risultante delle azioni scambiate tra i due corpi. Secondo Hertz la pressione massima p_max, e la semiampiezza del contatto b sono correlati al carico W tenendo conto della geometria del problema e delle costanti elastiche dei corpi.

La soluzione di Hertz può essere usata per rappresentare in prima approssimazione il contatto tra cilindro e semipiano ma non tiene conto della diversa cedevolezza del corpo al variare della posizione del cilindro rispetto alla fessura. Pertanto quando il cilindro transita in prossimità della bocca si realizza schematicamente una situazione come quella riportata in fig. 1 b con una distribuzione di pressioni non nota a priori.

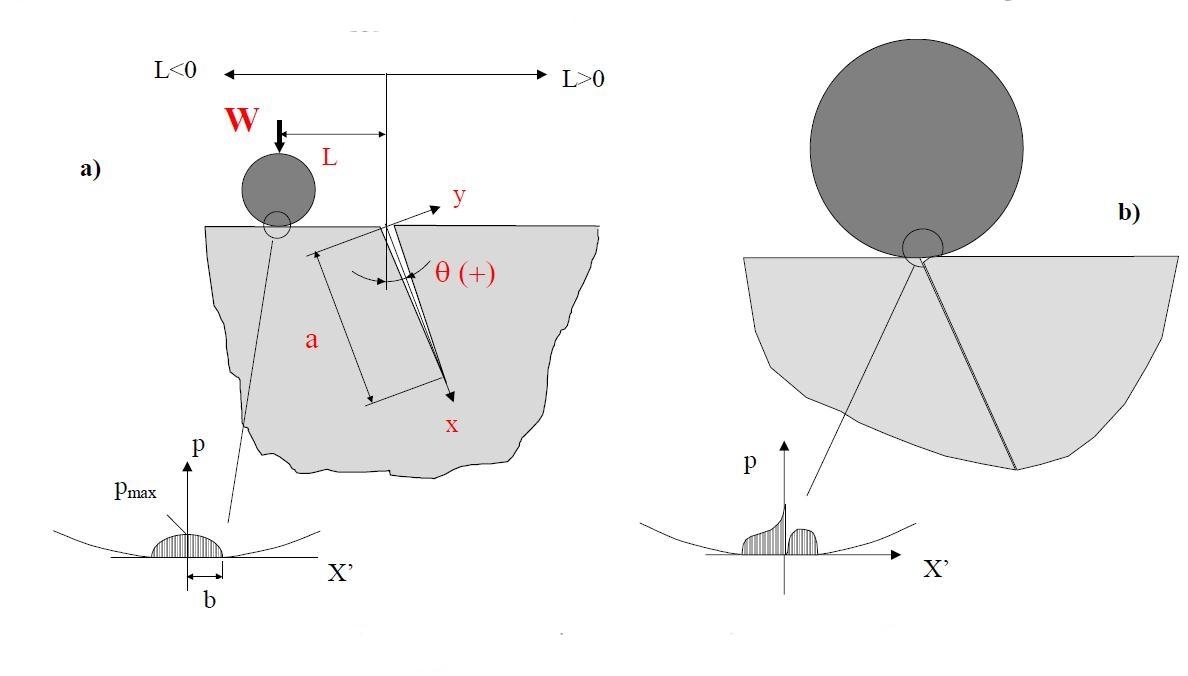
Fig. 1 - Rappresentazione schematica del problema

Tuttavia, sia che si consideri la distribuzione di pressioni che scaturisce dalla trattazione di Hertz del problema, sia che si consideri la distribuzione effettiva delle pressioni, l’andamento nominale delle tensioni nel corpo non fessurato, lungo il percorso della cricca, può essere calcolato approssimando la distribuzione di pressioni al contatto con una serie di forze puntuali. Utilizzando la soluzione analitica dovuta a Boussinesq [14] ed applicando il principio di sovrapposizione degli effetti si può in tal caso rappresentare lo stato tensionale come somma dei contributi delle singole forze. In questo lavoro l’effettiva distribuzione di pressioni è stata calcolata mediante una modellazione ad elementi finiti del contatto.

Non tenendo conto della non uniforme cedevolezza del corpo fessurato, le pressioni di contatto tra cilindro e semipiano possono essere descritte dalla distribuzione di Hertz (fig. 1a) di semiampiezza b. Per questa ipotesi di contatto è stata condotta un’analisi parametrica considerando diversi valori delle grandezze che influenzano il comportamento della fessura:

• inclinazione (θ),

• rapporto tra la dimensione della fessura e quella del contatto (a/b),

• posizione relativa del contatto (L/a),

• attrito tra le superfici di frattura (μ),

• attrito cilindro piano (φ).

I principali risultati sono riportati in [15,16]. Di seguito si richiamano alcuni andamenti rappresentativi. In fig. 2 sono riportati K_I e K_II in funzione di L/a, relativi ad un valore dell’angolo di inclinazione (θ = 40°), attrito moderato sulla fessura (μ=0.1), attrito nullo, cilindro piano, diversi valori del rapporto a/b. I dati sono normalizzati usando il valore:

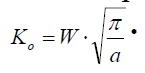
Questi grafici evidenziano come la fessura presenti modo misto di apertura in un limitato intervallo di valori di L/a (ca. 0 < L/a < 0,4) mentre essa è soggetta a puro modo II altrove. In ogni caso il modo II di frattura appare prevalente lungo tutto l’intervallo in cui il cilindro influenza la risposta della fessura.

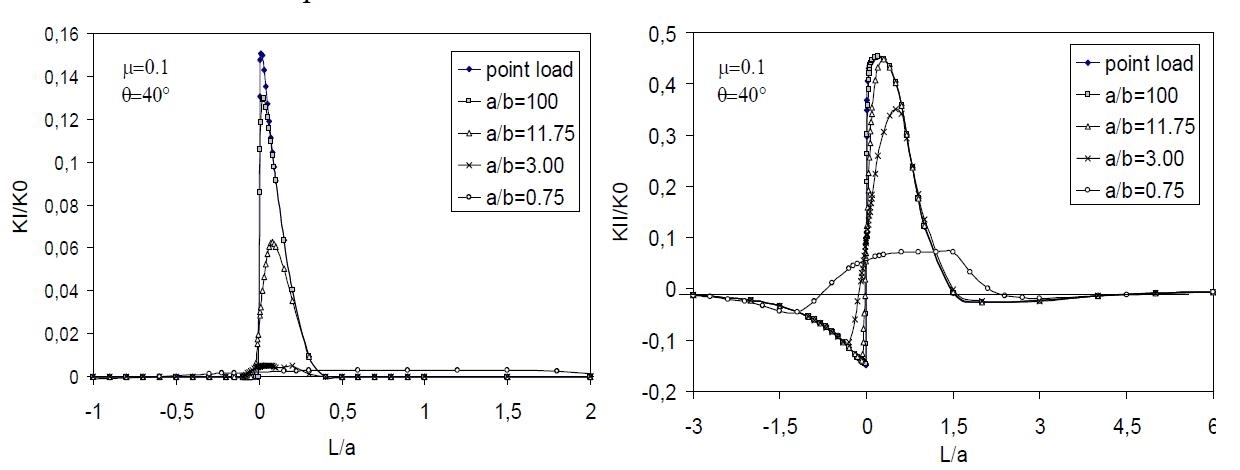
Fig. 2 - KI e KII vs L/a per differenti valori di a/b

Le forze di attrito si oppongono sempre al movimento relativo tra le superfici di frattura per cui l’aumento del coefficiente di attrito determina una diminuzione dei valori di FIS. Inoltre producono storie di carico differenti all’apice in dipendenza dalla direzione del cilindro, come si può osservare in fig. 3, in cui vengono riportati i luoghi K_I vs. K_II generati dal movimento del cilindro verso destra (+) e verso sinistra (-) per una fessura inclinata di θ = +70°.

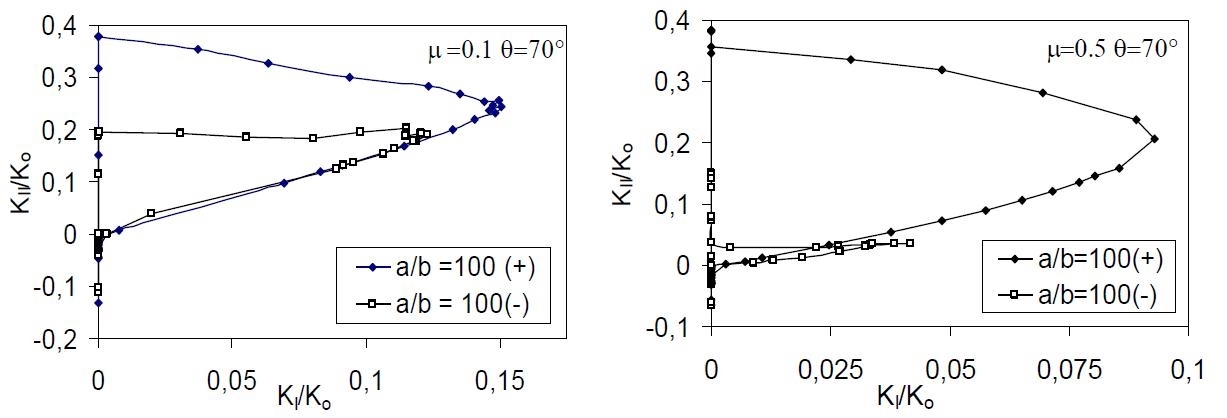
Fig. 3 - luoghi K_II vs K_I al variare del verso di percorrenza del cilindro. (a) attrito moderato μ=0.1, (b) attrito elevato μ=0.5.

L’effetto si traduce in una maggiore criticità per il caso in cui il cilindro è in moto verso destra e la fessura inclinata come in fig. 1. Questo tipo di risposta si manifesta in modo analogo per tutti gli angoli di inclinazione, accentuando le differenze all’aumentare del coefficiente di attrito e dell’angolo. Si osserva infine che una fessura inclinata di un angolo +θ quando il cilindro si muove verso sinistra è del tutto analoga ad una fessura inclinata di un angolo –θ con il cilindro in moto verso destra, pertanto l’analisi condotta per diversi angoli di inclinazione può essere utilizzata per studiare l’effetto dell’inclinazione positiva o negativa della fessura rispetto al movimento del cilindro. In fig. 4 è riportata la dipendenza dall’angolo di inclinazione dei valori ΔK_I e ΔK_II, misurati in un ciclo -∞ < L/a < +∞, per una condizione di attrito, evidenziando la maggior criticità di un’inclinazione positiva della fessura (fig. 1).

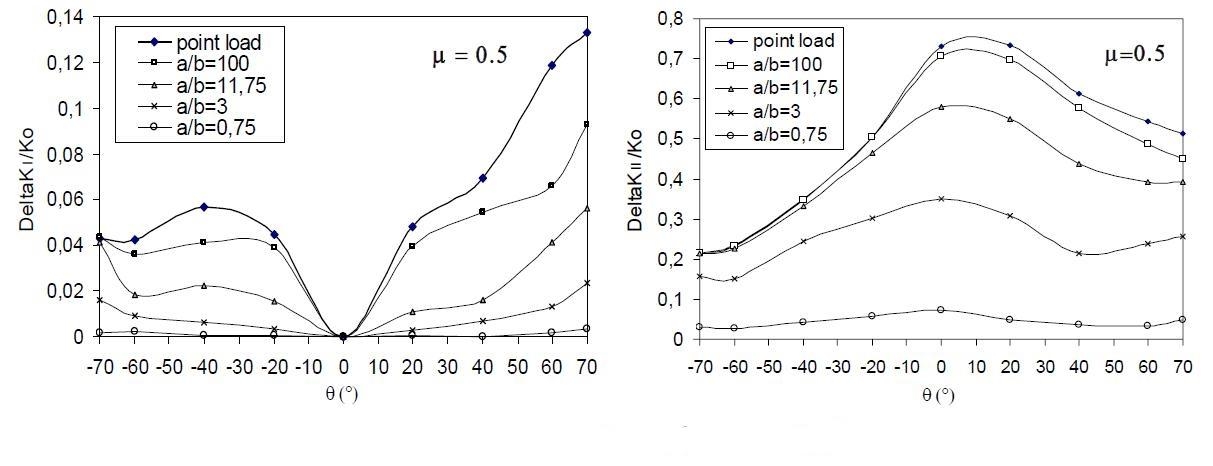
Fig. 4 - ΔKI e ΔKII vs. θ per μ = 0.5

Come anticipato l’effettiva distribuzione delle pressioni al variare della posizione del cilindro rispetto alla posizione della fessura non è nota a priori e può essere determinata mediante una modellazione ad elementi finiti del contatto.

INDICE

L’analisi ad elementi finiti è stata condotta con il codice Ansys 5.7, realizzando un modello bidimensionale, utilizzando elementi quadrilateri a quattro nodi (stiff42) per modellare i solidi ed elementi di contatto punto-superficie (contact48) per modellare il contatto tra cilindro e piano e tra le facce della fessura. Il modello è stato particolarmente affinato in prossimità della bocca della fessura per avere una accurata simulazione del contatto. In figura 5 è riportato il modello generale ed un dettaglio della regione del contatto.

La modellazione è stata condotta per un fessura inclinata di 60°, considerando diversi valori del rapporto a/b. Poiché le forze di attrito tra le superfici della fessura tendono a contrastare lo scorrimento relativo rendendo più rigida la risposta del semipiano fessurato al passaggio del cilindro sulla superficie, nella simulazione del contatto si è considerato come caso limite lo scorrimento senza attrito.

L’analisi è stata anche condotta per la condizione di attrito elevato μ=0,5 in modo da poter confrontare i risultati con quelli, basati sulla distribuzione Hertziana delle pressioni di contatto cilindro-semipiano, ottenuti in precedenti analisi [15,16].

Il modello è stata parametrizzato per adattare la mesh alle dimensioni dell’impronta, la quale dipende essenzialmente dal carico applicato e dal raggio del cilindro in contatto.

Riferendosi alla figura 2 si può osservare che l’intervallo nell’intorno della bocca della fessura entro cui il contatto cilindro semipiano si ripercuote in modo significativo sui valori di SIF della cricca può essere limitato entro –2 < L/a < 2. Sulla base di questo risultato la modellazione è stata condotta considerando diverse posizioni del cilindro entro l’intervallo suddetto.

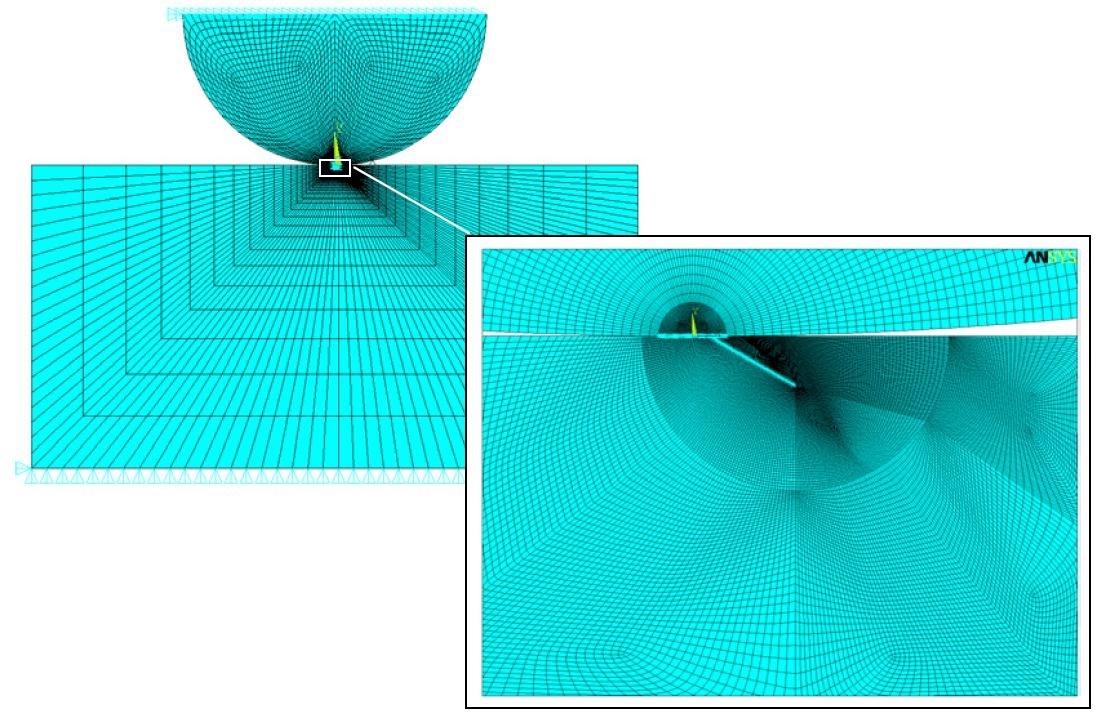
Fig. 5 - modello ad elementi finiti utilizzato per l’analisi

Da una prima analisi è stato possibile osservare che, fino ad una distanza L dalla bocca paragonabile alla dimensione dell’impronta, la distribuzione di pressioni nella regione di contatto tra cilindro e semipiano non risente della presenza della fessura, riproducendo la distribuzione predetta dall’analisi di Hertz.

La modellazione è stata quindi affinata considerando un nuovo intervallo di posizioni del cilindro: -4 < L/b < 4 ove b (cfr. fig.1) rappresenta la semiampiezza stimata del contatto.

La modellazione FEM permette di valutare oltre alla distribuzione di pressioni di contatto tra cilindro e semipiano, anche la configurazione assunta dalla fessura nelle varie condizioni di calcolo. In particolare per ognuna di queste sono stati acquisiti: l’estensione delle porzioni chiuse della fessura, i corrispondenti valori della distribuzione di pressione dovuta al contatto tra le superfici di frattura e l’andamento delle componenti di COD lungo tutta la fessura. Q

uesti dati verranno confrontati con quelli ottenuti utilizzando il metodo delle WF.

In figura 6 viene riportato l’andamento della distribuzione delle pressioni di contatto ottenute per diverse posizioni del cilindro rispetto alla bocca della fessura per un valore del rapporto a/b.

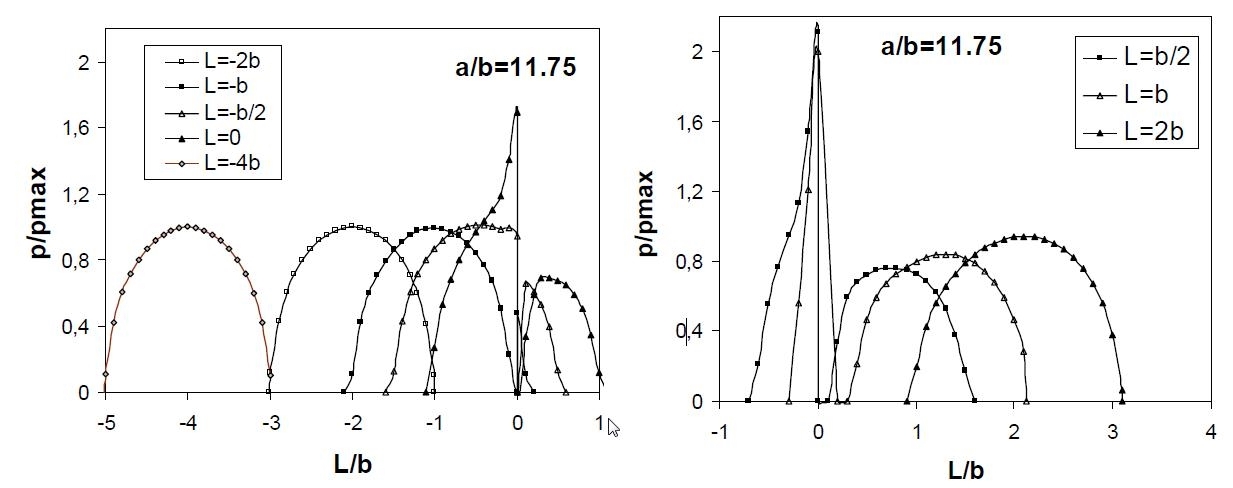
Figura 6 - andamento della distribuzione delle pressioni di contatto ottenute per diverse posizioni del cilindro rispetto alla bocca della fessura

I valori di pmax e di b sono rispettivamente la massima pressione e la semiampiezza teorica del contatto calcolate utilizzando la soluzione di Hertz. Ad una distanza dalla bocca della fessura pari a circa 2 volte l’impronta, la distribuzione di pressioni di contatto appare praticamente indisturbata dalla presenza della fessura e riproduce più o meno fedelmente la soluzione teorica di Hertz.

La perturbazione diviene particolarmente importante quando il cilindro si trova a valori di L ≥ 0, cioè quando il cilindro insiste sopra la fessura e carica la parte più cedevole del semipiano, in tal caso la forza viene scaricata in modo maggiore nella parte di semipiano ad L < 0 generando i picchi localizzati di pressione per L → 0^-.

INDICE

Partendo dalle distribuzioni di pressioni di contatto tra piano e cilindro ottenute dalla modellazione FEM ed anche da quelle calcolate utilizzando la soluzione di Hertz, è possibile determinare lo stato di tensione nominale nel corpo non fessurato.

La distribuzione di pressioni può essere in tal caso rappresentata da una serie di forze puntuali.

Come anticipato, utilizzando la soluzione di Boussinesq [14 ] per il carico puntuale ed il principio di sovrapposizione degli effetti si ottiene la distribuzione delle tensioni nominale lungo il percorso della fessura. In tal modo è possibile applicare il metodo delle WF per calcolare i FIS ed i valori di COD della fessura nelle condizioni più generali.

Si osserva innanzitutto che, poiché nel calcolo FEM sono state determinate anche le condizioni di parziale chiusura della fessura al variare della posizione del cilindro, può essere realizzato un confronto tra i risultati ottenuti con la modellazione FEM e con l’analisi WF in termini di distribuzione delle pressioni di contatto sulla porzioni chiuse della fessura ed in termini di COD della fessura stessa. Nelle figure seguenti è riportato tale confronto per un caso rappresentativo. I valori delle pressioni di contatto delle componenti di COD sono stati normalizzati usando rispettivamente i seguenti valori rappresentativi:

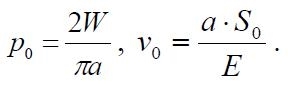
Si nota una quasi perfetta sovrapposizione degli andamenti ottenuti con i due approcci sia in termini di estensione delle porzioni chiuse della fessura, sia per quanto riguarda i valori di pressione e di COD. Ciò rappresenta un’ulteriore conferma della bontà dell’approccio iterativo proposto [12] per lo studio delle non linearità del problema.

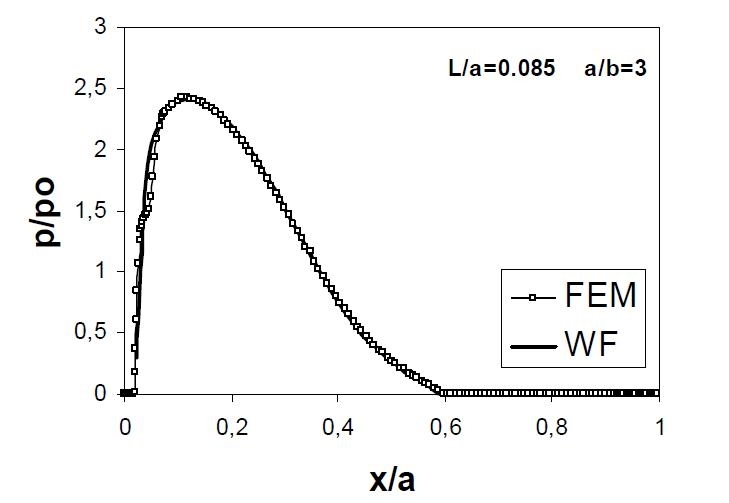
Fig. 7 - andamenti delle pressioni di contatto lungo la fessura ottenuti con i metodi FEM e WF

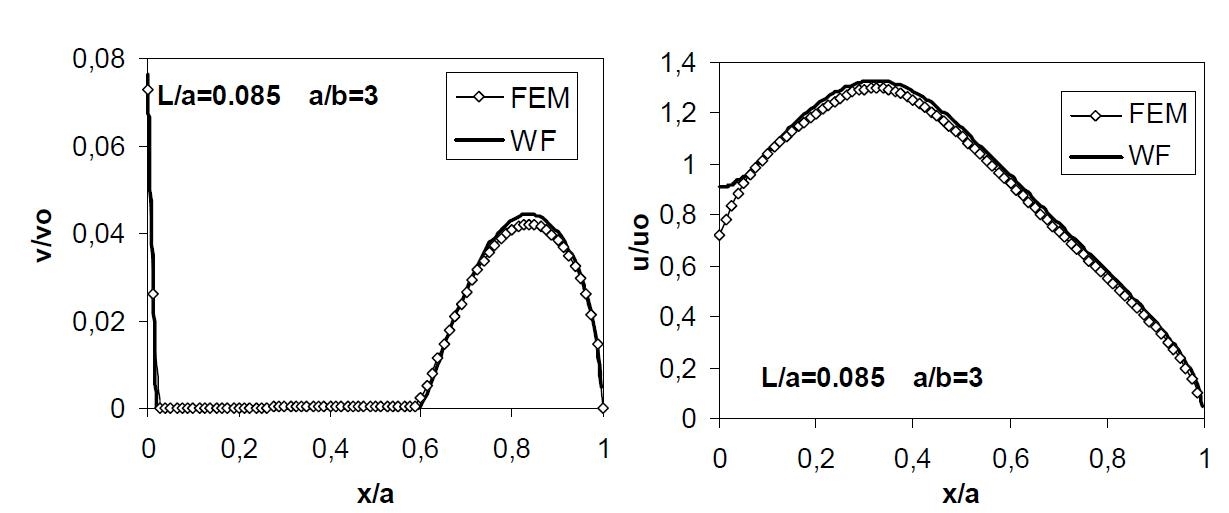
Fig. 8 - confronto tra i valori di e del COD v e COD u ottenuti con i metodi FEM e WF

Si può a questo punto passare ad analizzare i risultati in termini di FIS, ottenuti dall’applicazione del metodo delle WF considerando le due distribuzioni: Hertziana ed effettiva delle pressioni di contatto.

L’analisi è stata limitata all’intervallo di posizioni del cilindro entro cui la perturbazione locale dovuta alla cedevolezza del corpo fessurato risulta significativa. In figura 9 è riportato un esempio dei risultati ottenuti.

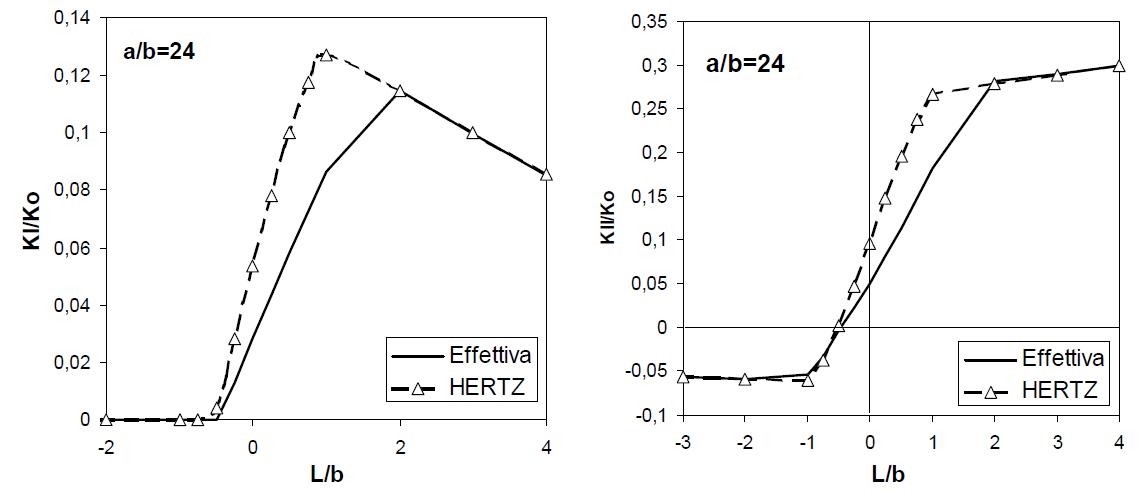
Fig. 9 - K_{I (eff)} e K_{I (HERTZ)} (a) e K_{II (eff)} e K_{II (HERTZ)} (b) in funzione della posizione del cilindro rispetto alla bocca della fessura.

Al variare della posizione di L la differenza tra le due soluzioni diviene significativa, soprattutto per K_I , in un limitato intervallo di posizioni del cilindro, al transito sulla bocca della fessura.

La soluzione basata sull’approccio elastico di Hertz fornisce un approssimazione per eccesso sia di K_I sia di K_II e questo fatto può essere interpretato considerando che nel caso reale le azioni del contatto si scaricano in modo predominante nella porzione di semipiano più rigida, in dipendenza della posizione della fessura.

Nell’analisi dell’effetto di una forza puntuale in moto [16] è stato dimostrato tuttavia che i valori massimi di FIS si raggiungono quando la forza si trova nella porzione più cedevole del semipiano.

Applicando il principio di sovrapposizione degli effetti i valori di FIS reale vengono ad essere quindi più bassi rispetto a quelli predetti usando la distribuzione di Hertz delle pressioni di contatto che non tiene conto della diversa cedevolezza del corpo e carica in modo indistinto la parte a destra ed a sinistra della bocca della fessura.

Gli andamenti rappresentati in figura 9 per uno specifico valore del rapporto a/b si ripropongono in modo sostanzialmente analogo al variare di questo.

In figura 10 è viene riportato l’andamento degli errori relativi sull’ampiezza dell’intervallo di FIS (ΔK_I e ΔK_II ) misurati in un ciclo -∞ < L < +∞.

L’errore che si commette è massimo quando la dimensione dell’area di contatto è paragonabile a quella della fessura mentre diminuisce fortemente per carichi molto concentrati (es. a/b=50) in cui la distribuzione di pressione si avvicina a quella da carico puntuale , o per impronte molto grandi in cui l’errore commesso localmente è mitigato della distribuzione dei carichi su un ampia porzione della superficie.

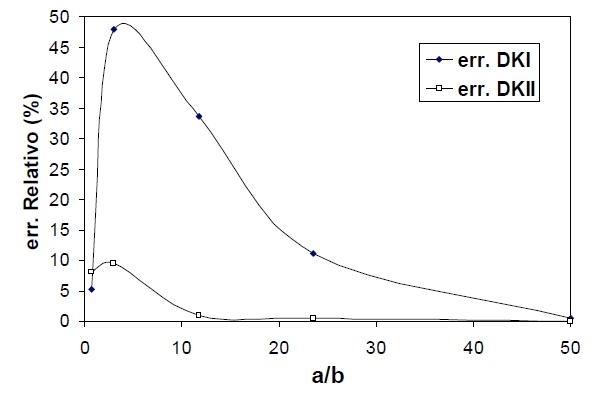
Fig. 10 - Errori relativi nella valutazione di ΔK_I e ΔK_II al variare del rapporto a/b

Per avere un’idea dell’effettivo ciclo di sollecitazione all’apice della fessura quando il cilindro si muove sulla superficie si può assumere una definizione di FIS equivalente e valutare un intervallo ΔK_eq = K_max – K_min , dove, osservando che K_I e K_II sono positivi nella regione di modo misto di sollecitazione,

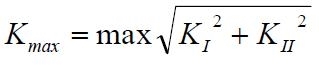
mentre K_min è il minimo di K_II dove K_I=0. In figura 11 sono riportati al variare di a/b i ΔK_eq ottenuti con le due ipotesi di distribuzione delle pressioni.

Come si può osservare l’errore introdotto nella semplificazione basata sull’analisi di Hertz risulta in tal caso molto contenuto e sempre in favore di sicurezza, essendo fornita una stima per eccesso delle condizioni di sollecitazione .

Sono state condotte anche analisi considerando l’effetto della presenza di forze d’attrito tra le superficie della fessura in contatto. I risultati ottenuti hanno evidenziato che queste forze di attrito, opponendosi allo scorrimento delle superfici rendono meno disuniforme la cedevolezza del corpo fessurato in funzione della posizione del cilindro. Pertanto la differenza tra l’ipotesi di distribuzione Hertziana delle pressioni e quella effettiva risulta ancora più contenuta.

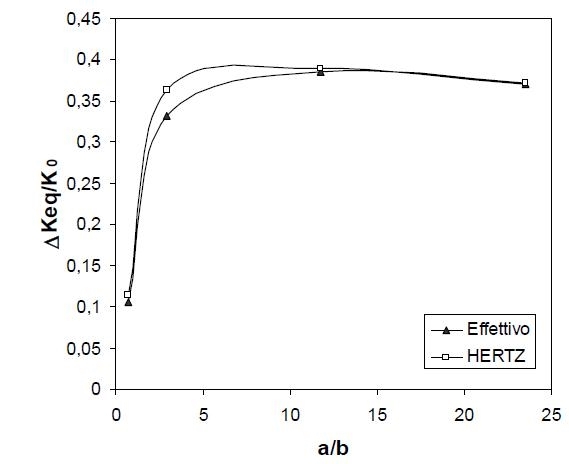
Fig. 11 - ΔK_eq in funzione del rapporto a/b per le due ipotesi di calcolo

INDICE

Mediante il metodo delle WF è stata affrontata l’analisi dell’importanza della non uniforme cedevolezza del corpo recante una fessura obliqua, nel contatto con un altro corpo in moto sulla sua superficie.

L’utilizzo di una modellazione FEM del corpo fessurato e del contatto con un cilindro in moto sulla superficie si è reso necessario in quanto la distribuzione delle pressioni di contatto quando il cilindro transita sulla bocca della fessura non è nota a priori e viene usualmente approssimata con la distribuzione di Hertz.

L’applicazione del metodo delle WF si è rivelata molto efficiente per valutare proprio il grado di approssimazione introdotto nell’utilizzo della distribuzione di Hertz che trascura la cedevolezza locale del corpo.

Si è potuto dimostrare che l’errore che viene commesso è relativamente modesto, è comunque in favore di sicurezza e dipende dalle condizioni di attrito tra le facce della fessura.

Dal confronto tra le condizioni di apertura della fessura simulate tramite FEM e calcolate con le WF si è ottenuto inoltre un’ulteriore conferma della bontà dell’algoritmo iterativo basato sulle WF e messo a punto per lo studio delle condizioni di parziale chiusura della fessura.

INDICE