Principi generali di analisi acustica

AREA I - ARTE TECNICO-SCIENTIFICA (ATS)

Cap. ATS-J01 - Acustica - Pag. ATS-J01.06

Gli argomenti trattati sono stati inseriti da Ing. Arch. Michele Cuzzoni nel 2009 - © Copyright 2007- 2024 - e sono desunti dalla documentazione indicata in Bibliografia a fondo pagina

---

 

 

 

INDICE:

 

• Premessa

• Connessione di sistemi dinamici in MATLAB

• Risposta in frequenza

• Relazioni tra risposte nel tempo e in frequenza

• Analisi di stabilità e stabilizzazione con Nyquist

• Conclusioni

 

Scopo di questi appunti: imparare a usare MATLAB per analizzare le risposte di sistemi dinamici LTI a tempo continuo nel dominio della frequenza e per fare semplici analisi di stabilità di sistemi retroazionati.

Contenuto del testo:

• sistemi interconnessi in MATLAB;

• calcolo di risposte in frequenza;

• correlazione con il dominio del tempo;

• diagrammi di Bode e polari;

• analisi di stabilità di sistemi retroazionati (nelle ipotesi di Bode e non);

• conclusioni.

 

INDICE

 

Esempi (serie, parallelo, retroazione):

» S1=ss(-2,1,1,0);

» S2=tf(1,conv([10 1],[1 1]));

» S3=tf(0.1,[5 1]);

» S4=tf(S1+S2*S3/(1+S2*S3))

Transfer function:

s^6 + 2.6 s^5 + 2.332 s^4 + 0.8806 s^3 + 0.1628 s^2 + 0.01476 s +0.00052

---------------------------------------------------------------

s^7 + 4.6 s^6 + 7.53 s^5 + 5.534 s^4 + 1.905 s^3 + 0.3274 s^2 +0 .02732 s + 0.00088

INDICE

 

Si calcoli una risposta in frequenza con la definizione (immagine tramite la FdT del semiasse I+) e a plottarne modulo (in scala logaritmica) e fase (in gradi) avendo per ascissa (logaritmica) la pulsazione.

La funzione polyval serve a valutare un polinomio; loglog e semilogx[y] sono di funzionamento intuitivo.

» num=[10 1];

» den=conv([1 1],[100 1]);

» j=sqrt(-1);

» w=logspace(-4,2,500);

» RF=polyval(num,j*w)./polyval(den,j*w);

» mRF=abs(RF);

» fRF=angle(RF);

» subplot(211); loglog(w,mRF);

» subplot(212); semilogx(w,fRF/pi*180);

 

 

Altro esempio: si calcoli e plotti modulo e fase della risposta in frequenza di:

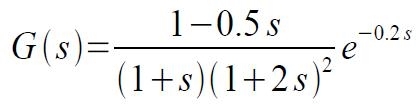
» num=[-5 1]; den=conv([1 1],conv([2 1],[2 1])); d=0.2;

» j=sqrt(-1);

» w=logspace(-4,2,500);

» RF=polyval(num,j*w)./polyval(den,j*w).*exp(-d*j*w);

» mRF=abs(RF);

» fRF=angle(RF);

» fRFu=unwrap(fRF); (evita la riduzione al 1° giro)

» subplot(211); loglog(w,mRF);

» subplot(212); semilogx(w,fRF/pi*180,w,fRFu/pi*180);

Risultato:

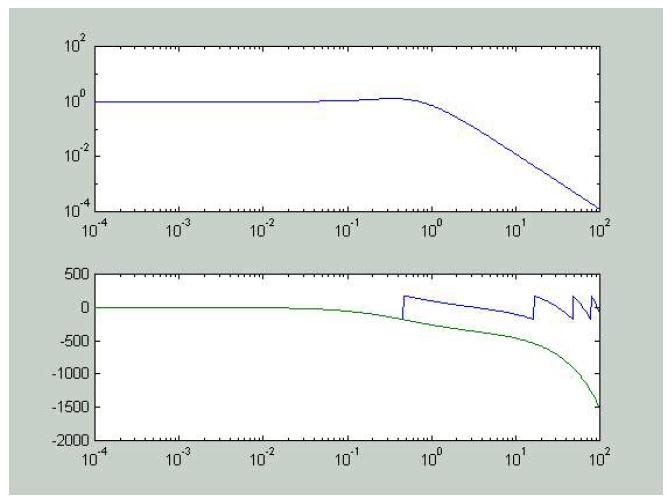
Si prendano adesso le due funzioni di trasferimento:

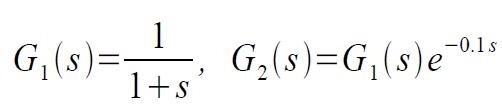
si calcolino le risposte in frequenza e si rappresentino nel piano complesso come curve punteggiate dalla pulsazione:

» num=1; den=[1 1]; d=0.1;

» w=logspace(-3,6,1000);

» RF1=polyval(num,j*w)./polyval(den,j*w);

» RF2=RF1.*exp(-d*j*w);

» plot(real(RF1),imag(RF1),real(RF2),imag(RF2));

 

Risultato:

 

INDICE

 

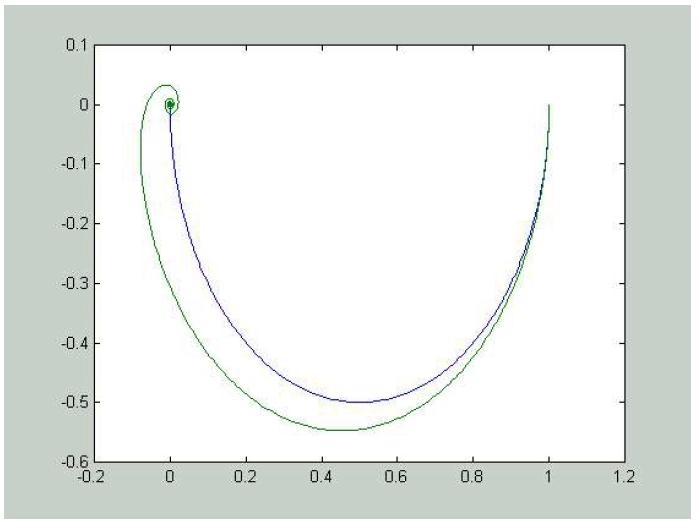
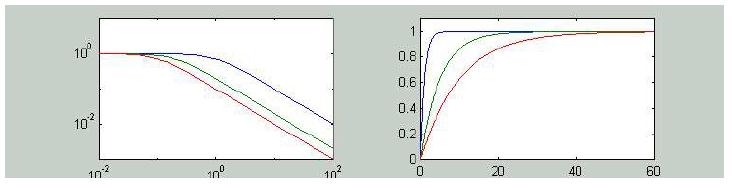
Relazione tra banda passante e velocità di risposta:

» w=logspace(-2,2);

» m1=abs(1./polyval([1 1],sqrt(-1)*w));

» m2=abs(1./polyval([5 1],sqrt(-1)*w));

» m3=abs(1./polyval([10 1],sqrt(-1)*w));

» t=0:0.1:60;

» y1=step(tf(1,[1 1]),t);

» y2=step(tf(1,[5 1]),t);

» y3=step(tf(1,[10 1]),t);

» subplot(121); loglog(w,m1,w,m2,w,m3);

» axis([w(1) w(end) 1e-3 10]);

» subplot(122); plot(t,y1,t,y2,t,y3);

» axis([t(1) t(end) 0 1.1]);

 

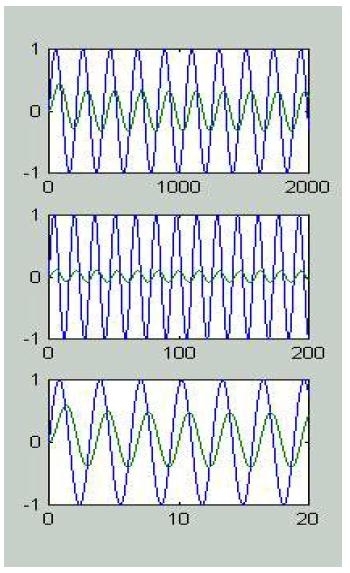
Misura di modulo e sfasamento della risposta in frequenza ad una data pulsazione:

» G=tf([10 1],conv([1 1],[100 1]));

» w1=0.03; » w2=0.4; » w3=2;

» t1=0:2000;

» t2=0:0.1:200;

» t3=0:0.01:20;

» u1=sin(w1*t1);

» u2=sin(w2*t2);

» u3=sin(w3*t3);

» y1=lsim(G,u1,t1);

» y2=lsim(G,u2,t2);

» y3=lsim(G,u3,t3);

» subplot(311); plot(t1,u1,t1,y1);

» subplot(312); plot(t2,u2,t2,y2);

» subplot(313); plot(t3,u3,t3,y3);

» subplot(313); plot(t3,u3,t3,10*y3);

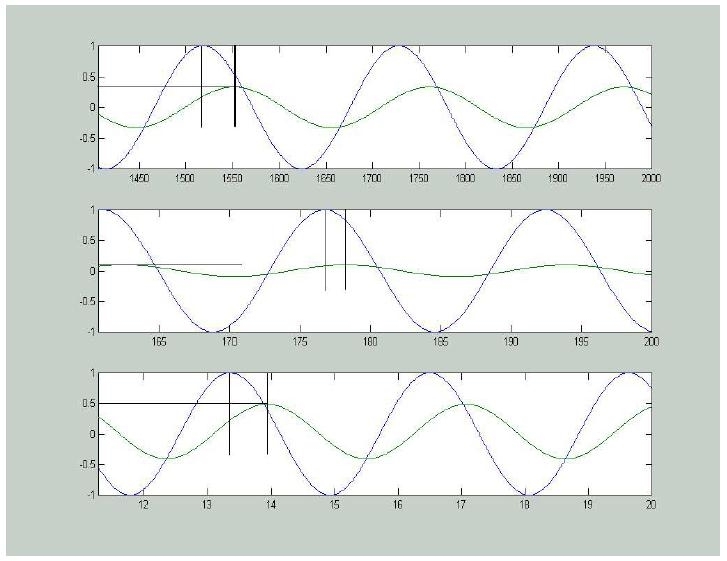
Usando lo strumento di zoom si evidenzino le ultime oscillazioni dei movimenti forzati che si sono calcolate e si valutino:

• l'ampiezza |Y| dell'uscita e

• la distanza temporale D tra i massimi corrispondenti di questa e dell'ingresso (ovviamente col segno + se in anticipo, - se in ritardo).

 

Risultati:

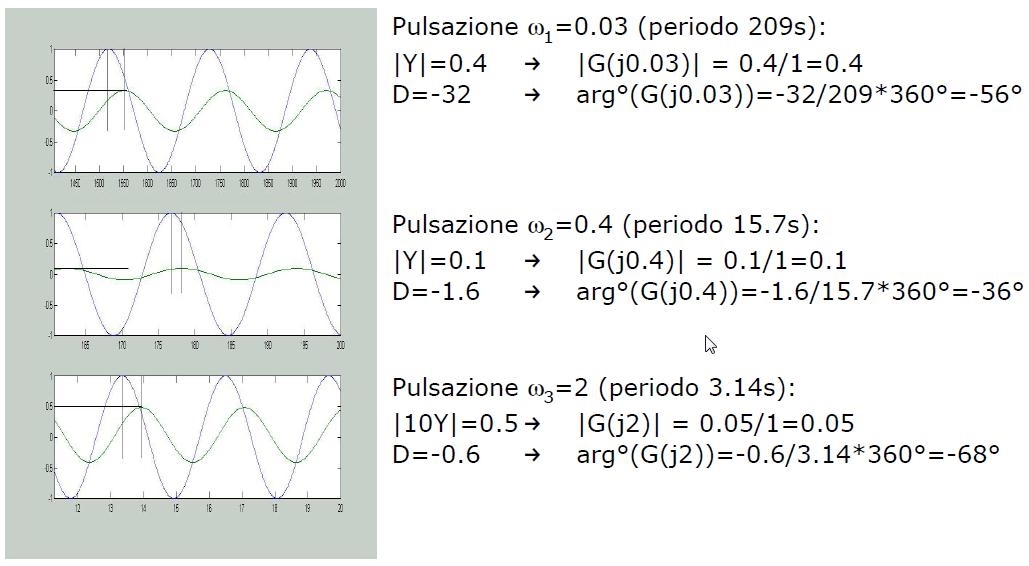
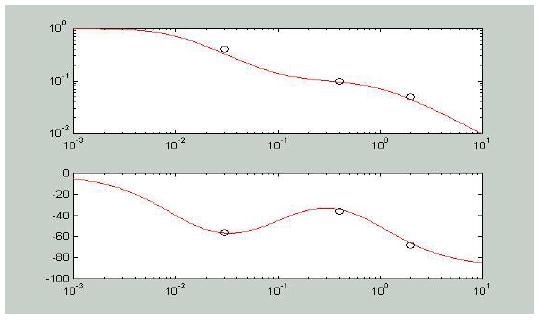
Si verifichi osservando la risposta in frequenza calcolata:

» w=logspace(-3,1,1000); j=sqrt(-1);

» RF=polyval([10 1],j*w)./polyval(conv([1 1],[100 1]),j*w);

» m=abs(RF); f=angle(RF)/pi*180;

» subplot(211);

» loglog(w,m,'r',[w1 w2 w3],[0.4 0.1 0.05],'ok');

» subplot(212);

» semilogx(w,f,'r',[w1 w2 w3],[-56 -36 -68],'ok');

Tre comandi utili:

Il comando bode calcola e/o traccia a video i diagrammi di Bode;

Il comando nyquist calcola e/o traccia a video il diagramma di Nyquist;

Il comando margin calcola i margini di fase e guadagno data la funzione di trasferimento d'anello e/o li mostra a video sui relativi diagrammi di Bode.

 

INDICE

 

Un paio di esempi semplici:

Analizzare con Nyquist la stabilità del sistema di controllo in retroazione negativa con P(s)=1/((s+10)(s-3)) e R(s)=1 (è instabile);

determinate un regolatore in retroazione (negativa) R(s) che renda asintoticamente stabile il sistema in anello chiuso;

 

ATTENZIONE:

• non si è nelle ipotesi di Bode e si deve usare il criterio di Nyquist,

• non si può cancellare il polo instabile; 

SOLUZIONE: ad esempio R(s)=50, che fa fare al diagramma di Nyquist della risposta in frequenza di L=RP un giro antiorario attorno al punto -1.

 

INDICE

 

 

• Si è visto come rappresentare sistemi interconnessi e come calcolare e rappresentare risposte in frequenza in MATLAB.

• Si è correlato, in modo semplice e non esaustivo, i domini del tempo e della frequenza.

• Si è fatta analisi di stabilità nelle ipotesi di Bode e non, vedendo anche un semplice esempio di stabilizzazione con uso del criterio di Nyquist.

 

INDICE

 

---

Portale "Ingegneria e Campanologia" - Autore - Sommario - Mappa del Sito - Home

Bibliografia

 

Bib-TS-197 - Appunti di Laboratorio di Fondamenti di Automatica, Terza esercitazione. Politecnico di Milano, AA. 2004 / 2005

 

 

TOP

 

---