Portale "Ingegneria e Campanologia" - Autore - Sommario - Mappa del Sito - Home
Principi generali di analisi acustica
AREA I - ARTE TECNICO-SCIENTIFICA (ATS)
Cap. ATS-J01 - Acustica - Pag. ATS-J01.05
Gli argomenti trattati sono stati inseriti da Ing. Arch. Michele Cuzzoni nel 2009 - © Copyright 2007- 2024 - e sono desunti dalla documentazione indicata in Bibliografia a fondo pagina
Analisi in frequenza di segnali - Bande
Secondo il teorema di Fourier, una funzione periodica y(t) è sviluppabile in una serie costituita da un termine costante
A0 e da una somma di infinite sinusoidi:
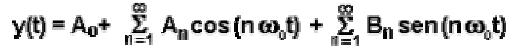
le cui frequenze fn sono multiple intere della frequenza f0 della funzione data (nota che ω=2πf) :
e di ampiezze An e Bn calcolabili secondo le seguenti formule:
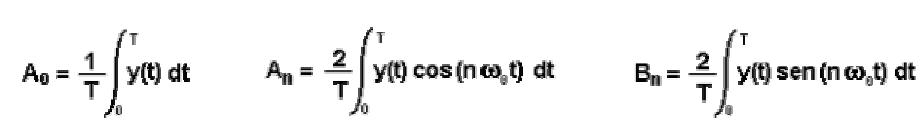
Un segnale di particolare interesse è l'onda quadra per via dei numerosi impieghi che la caratterizzano come il clock nei circuiti digitali e le portanti numeriche nei sistemi di telecomunicazioni.
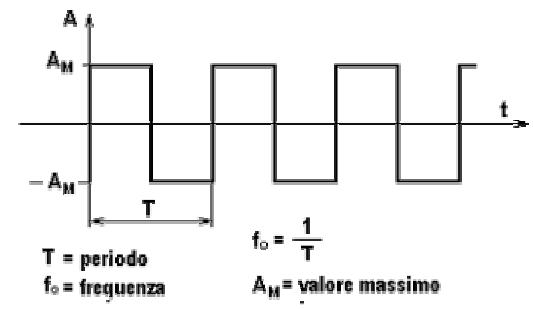
Dall'applicazione delle formule della serie di Fourier risulta che l'onda quadra in oggetto è costituita dalla somma di infinite sinusoidi, dette armoniche, di frequenza multipla intera di fo e di ampiezza data dai valori:
Alla luce dei coefficienti di Fourier appena trovati la funzione onda quadra, sviluppata in serie di Fourier, risulta espressa come segue:
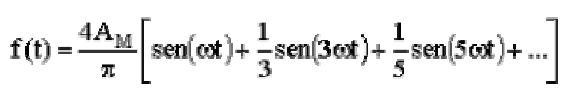
Lo spettro di ampiezza del segnale risulta allora quello riportato in figura: (nota che poiché la serie di Fourier è definita per n che va da 0 a +∞ lo spettro in frequenza è monolatero definito in frequenza da 0 a +∞)
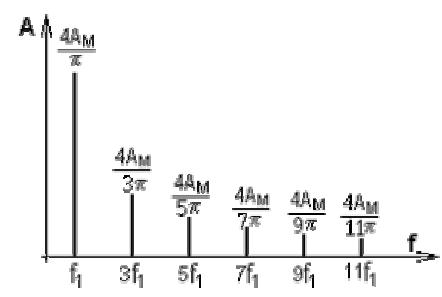
Le funzioni aperiodiche possono essere concepite come funzioni periodiche allorché il periodo tende a crescere fino all'infinito. Allora la distanza fra due righe dello spettro a righe tende a zero e lo spettro diventa a bande continue. La Serie di Fourier si trasforma in un integrale che assume il nome di Trasformata di Fourier, che rappresenta la distribuzione continua delle frequenze presenti in un segnale aperiodico. Ecco che ad un segnale x(t) nel tempo viene associato un segnale X(f) in frequenza:
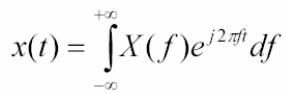e viceversa
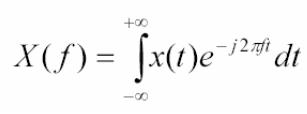
Ecco alcune proprietà che della trasformata di Fourier (TDF):
-
Valori nell'origine: la TDF in f = 0 è uguale all'integrale del segnale nei tempi. Il segnale in t = 0 è uguale all'integrale della TDF nelle frequenze.
-
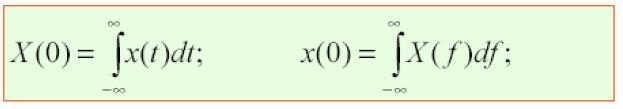
Traslazione nei tempi: la TDF del segnale ritardato è uguale a quella del segnale originale moltiplicata per un esponenziale complesso
Nota: una traslazione nel dominio temporale corrisponde ad una variazione della fase in quello frequenziale.
-
Derivazione nei tempi: la TDF del segnale derivato nel tempo è uguale a quella del segnale originale moltiplicata per j 2 π f:
-
Moltiplicazione nelle frequenze: la TDF inversa del prodotto delle TDF di due segnali è uguale all'integrale di convoluzione dei segnali nei tempi. L'integrale di convoluzione è un operatore utilizzato per descrivere come vengono modificati i segnali quando passano attraverso sistemi lineari tempo-invarianti.
-
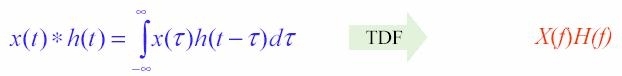
Relazione di Parseval: l'energia di un segnale è uguale all'integrale del modulo quadrato della sua TDF:
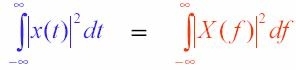
Nota che poiché l’integrale di Fourier è definito da -∞ a +∞ lo spettro in frequenza è bilatero definito in frequenza tra -∞ a +∞ e, per le ampiezze, simmetrico rispetto all’asse delle ordinate.
-
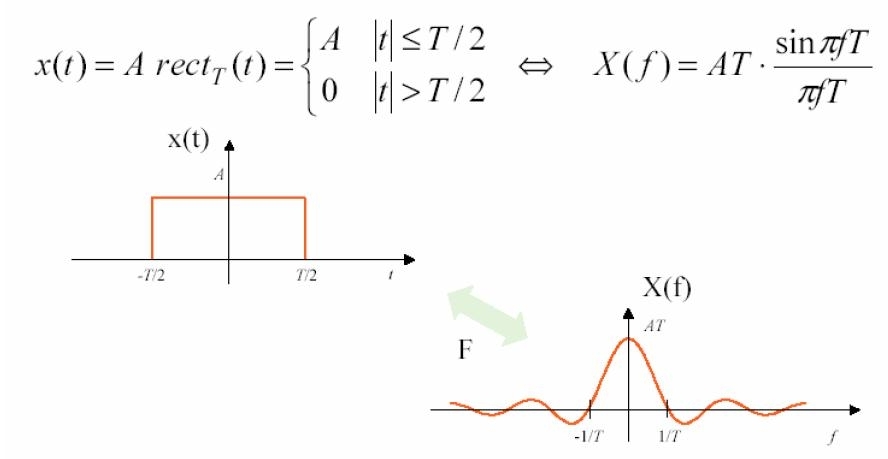
La funzione rect (rettangolo)
-
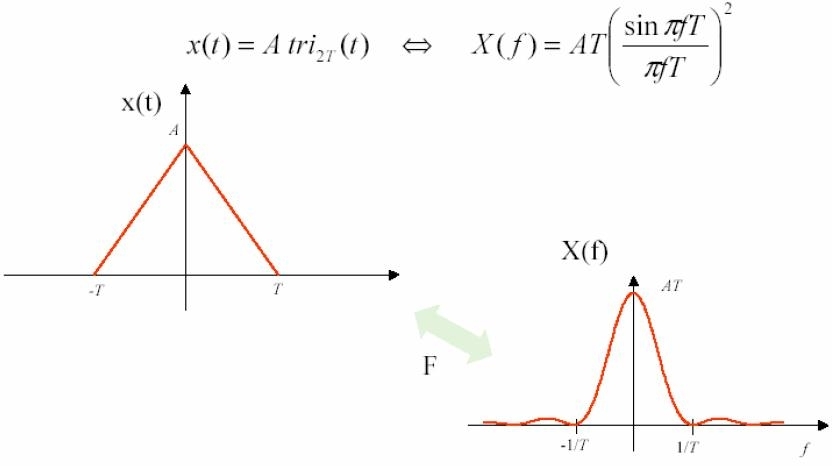
La funzione triangolo
-
La funzione costante
-
La funzione impulsiva
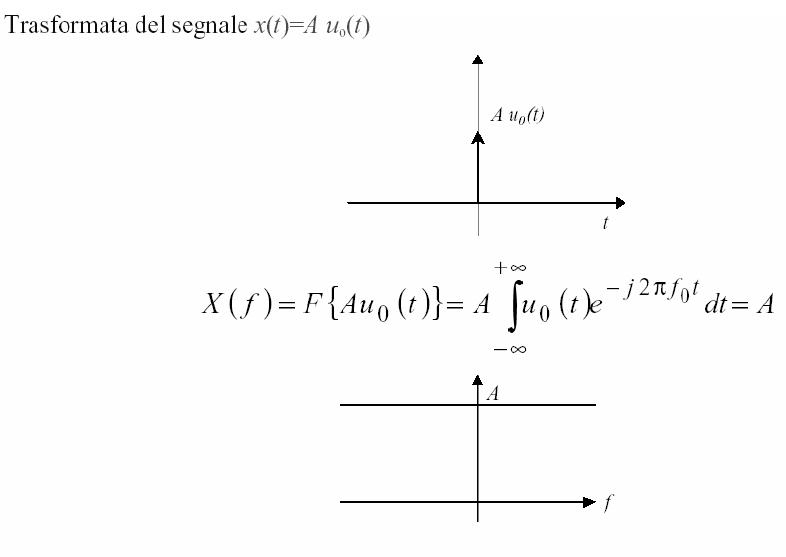
Viene definita banda (B) del segnale x(t) l’intervallo di frequenze (misurato sul semiasse positivo dello spettro bilatero) all’interno del quale X(f) assume valori diversi da 0.
Molto spesso X(f) è a rigore diversa da 0 da -∞ a +∞. In questo caso la banda corrisponde all’intervallo di frequenza in cui X(f) è “significativamente” diversa da 0.
Operativamente, nella definizione di banda, si considerano due classi di segnali: segnali passa-basso e segnali passa-banda (questi ultimi non avendo la componente continua, ovvero a frequenza nulla, hanno nel tempo valor medio nullo).
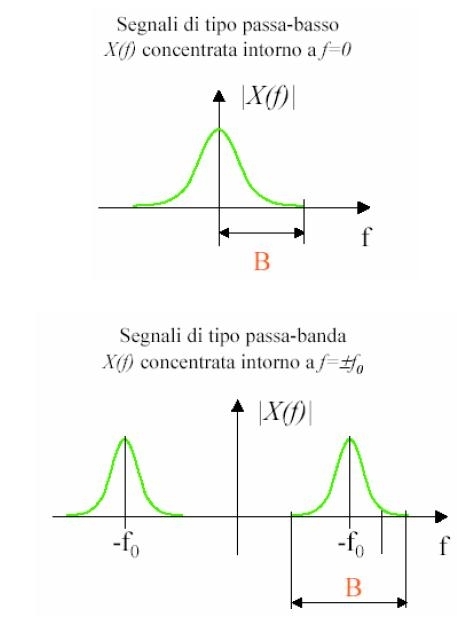
• Segnali sismici 1 ÷ 200 Hz
• Elettrocardiogramma 0.05 ÷ 100 Hz
• Segnali audio 20 Hz ÷ 15 kHz
• Segnali video 50 Hz ÷ 4,2 MHz
• Segnali radio AM 540 KHz ÷ 1600 kHz
• Segnali radio FM 88 MHz ÷ 108 MHz
• Video VHF 54 MHz ÷ 60 MHz
• Video UHF 470 MHz ÷ 806 MHz
• Telefonia cellulare 1 824 MHz ÷ 891.5 MHz
• Video satellitare 3.7 GHz ÷ 4.2 GHz
• Comunicazioni a microonde 1 GHz ÷ 50 GHz
Per modulazione si intende la tecnica di trasmissione di un segnale elettromagnetico rappresentante un'informazione x(t) per mezzo di un altro segnale elettromagnetico detto portante y(t), tipicamente a frequenze molto maggiori.
L'onda portante y(t) è un'onda elettromagnetica con caratteristiche (frequenza, fase, ampiezza) ben determinate e note a priori di cui si modificano una delle proprietà (frequenza, fase o ampiezza) in funzione del segnale modulante x(t) al fine di ottenere un segnale modulato z(t).
z(t) conterrà in se' l’informazione del segnale modulante x(t), che tipicamente è di tipo passa-basso, ma z(t) sarà di tipo passa-banda con frequenze centrate attorno a quelle della portante y(t).
I segnali da modulare possono rappresentare le informazioni più diverse: audio, video, dati. Il motivo per cui si utilizza la modulazione risiede nel fatto che i segnali rappresentanti le informazioni da trasmettere sono in prevalenza di natura passa-basso (il loro contenuto spettrale è concentrato per lo più a basse frequenze, vedi 2.6.2), mentre i canali trasmissivi che più comunemente si utilizzano sono di natura passa-banda. Occorre quindi convertire in frequenza, mediante tale operazione, lo spettro del segnale elettromagnetico rappresentante l'informazione.
L'impiego di questa tecnica permette di trasmettere segnali elettrici (e quindi le informazioni che essi rappresentano) a grande distanza.
In trasmissione il circuito responsabile della modulazione è detto modulatore mentre in ricezione il circuito che recupera dal segnale modulato il segnale informativo è detto demodulatore. Un apparecchiature che trasmette e riceve segnali modulati ha dunque un MODEM (MOdulatore/DEModulatore).
Nel campo delle modulazioni analogiche ricordiamo la AM - (Amplitude Modulation) modulazione di ampiezza e la FM - (Frequency Modulation) modulazione di frequenza che incontriamo nella vita quotidiana tramite la radio.
L'AM è stato il primo metodo usato per trasmettere programmi radio ed è impiegata nelle trasmissioni radio a onde corte su lunghe distanze e nelle trasmissioni della parte video dei programmi televisivi. Le stazioni radio AM commerciali operano a frequenze fra i 540 e i 1600 kHz, separate fra loro di 10 kHz.
Le frequenze dell'onda portante usate per la televisione vanno da 55 a 210 MHz circa. In questa banda vi è spazio disponibile per circa 30 stazioni televisive, ciascuna delle quali usa una larghezza di banda di circa 5 MHz.
La formula che esprime un segnale modulato in ampiezza è la seguente:
dove
è
l'andamento temporale del segnale modulato,
è l'andamento temporale del segnale modulante,
è
la sinusoide portante (dove
è
la tensione di picco della portante ed m è la profondità di modulazione).
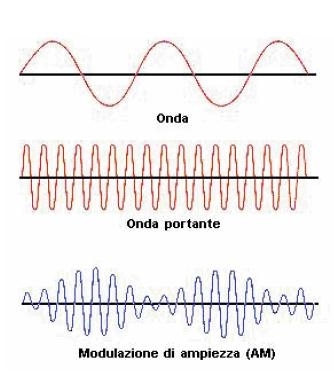
Esempio di modulazione di ampiezza con segnale modulante x(t) e portante y(t) entrambi di tipo sinusoidale ma con frequenza di x(t) << frequenza y(t)
Nelle trasmissioni a modulazione di frequenza (FM) l'ampiezza del segnale portante è mantenuta costante. La sua frequenza viene alterata a seconda delle variazioni nel segnale audio modulante che si vuole trasmettere. La tecnica della modulazione di frequenza fu sviluppata da H. Armstrong negli anni '30, per cercare di rimediare all'interferenza e al rumore che poteva rendere le trasmissioni AM di difficile ricezione. Alle stazioni radio FM commerciali sono state assegnate frequenze nel range che varia da 88 a 108 MHz e le stazioni sono distanziate di 200 kHz fra loro.
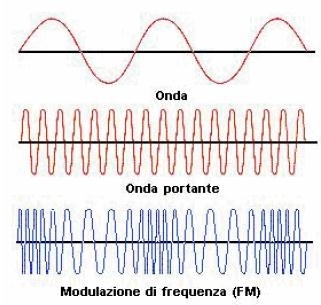
Esempio di modulazione di frequenza con segnale modulante x(t) e portante y(t) entrambi di tipo sinusoidale ma con frequenza di x(t) << frequenza y(t)
Portale "Ingegneria e
Campanologia" -
Autore -
Sommario
- Mappa del Sito -
Home
Bib-TS-196 - Appunti di Esercitazioni di Ing. Saponara del Corso: Autronica (LS Veicoli Terrestri) a.a. 2005/2006