Portale "Ingegneria e Campanologia" - Autore - Sommario - Mappa del Sito - Home
Metallurgia dei metalli e delle leghe
AREA I - ARTE TECNICO-SCIENTIFICA (ATS)
Cap. ATS-H02 - Metallurgia - Pag. ATS-H02.13
Gli argomenti trattati sono stati inseriti da Ing. Arch. Michele Cuzzoni nel 2012 - © Copyright 2007- 2025- e sono desunti dalla documentazione indicata in Bibliografia a fondo pagina
-
Operazioni necessarie per effettuare una analisi di immagine quantitativa
-
Misura delle grandezze stereologiche di interesse e analisi statistica
Uno dei principali obbiettivi dell’analisi quantitativa di immagine applicata alla pp metallurgia è di riuscire a legare la microstruttura della lega in esame con le sue proprietà meccaniche. Ciò è possibile solo se si effettuano delle misure “obiettive”, si trattano queste misure mediante computer e si effettua una analisi statistica su un gran numero di osservazioni. La metallografia quantitativa permette di analizzare in modo quantitativo differenti strutture presenti nella lega in esame: inclusioni, dimensioni dei grani, morfologie di corrosione, morfologie di frattura, forma degli agglomerati etc.
In particolare per quanto riguarda la frattografia quantitativa, si potrà procedere in due modi differenti: analisi della superficie di frattura oppure analisi del profilo della frattura stessa.
Alla base di queste procedure vi è la stereologia, ovvero la scienza che consente la formulazione di relazioni funzionali e la deduzione quantitativa delle caratteristiche di un sistema eterogeneo a partire dall’analisi effettuata su poche sezioni del sistema stesso. Essa può essere considerata:
• una geometria, perché definisce sui sistemi materiali delle caratteristiche geometriche;
• una statistica, in perché acquisisce i dati attraverso tecniche di campionamento.
Attraverso la stereologia è possibile determinare ad esempio:
• la grandezza media dei grani per ciascuna fase
• la superficie di interfaccia comune a due grani
• la superficie specifica dei suoi grani
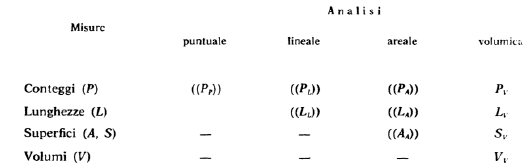
Le principali grandezze stereologiche sono esposte nella tabella seguente.

L’analisi di tipo volumetrico è priva di senso in stereologia, in quanto tale scienza deduce le proprietà volumetriche da indagini effettuate su sezioni piane.
Il sezionamento operato nell’analisi stereologica, provoca la diminuzione di un ordine di grandezza dell’ente geometrico, per cui i volumi vengono analizzati come aree (A), le superfici come linee (L), le linee come punti (P) ed i punti, per così dire, spariscono e non sono identificabili.
L’analisi stereologica può essere:
• areale
• lineare
• puntuale
Qualsiasi grandezza stereologica può essere ricondotta ai conteggi fondamentali (PA, PL, PP). A seconda che si imponga l’analisi di una area nota, di una linea nota o un numero totale di punti si possono effettuare diverse misure.
Per effettuare una analisi stereologica si sovrappone ad una sezione piana del sistema da analizzare un sistema predisposto di aree, linee, punti che costituisce la cosiddetta griglia. I moderni sistemi di analisi di immagine computerizzati superano certamente questa metodologia, che, comunque, resta almeno concettualmente alla base. Dopo tale sovrapposizione si effettua il conteggio degli elementi ritenuti di interesse.
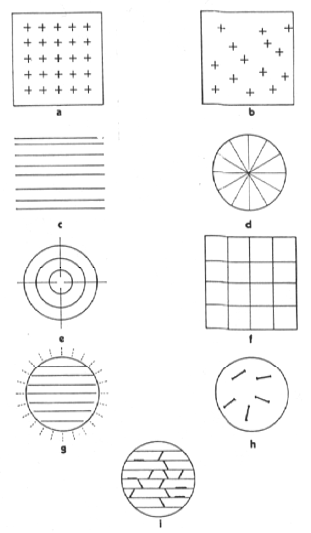
Tipi di griglie: a) puntuale; b) puntuale non ordinata; c) segmentaria parallela; d) segmentaria stellare; e) circolare; f) reticolare quadrata; g) composita; h) di Chalkey; i) altro tipo di griglie.
E’ possibile fornire un elenco succinto delle misure rilevabili sul piano di sezionamento mediante impiego di griglie. Conteggi:
1. Conteggio dei punti (Pp).
Rappresenta il metodo più agevole per la valutazione della frazione volumica; si utilizza una griglia reticolare quadrata il cui numero di nodi è in rapporto all’area osservata; generalmente 16 nodi.
2. Conteggio delle intersezioni (PL)
Può essere applicato separatamente ad ogni tipo di contorno sulla sezione lucidata; nel caso di sinterizzati si possono scegliere contorni di grani o contorni di pori al fine di valutare la superficie specifica della interfaccia prescelta.
3. Conteggio delle tangenti (TA)
Si applica alle interfacce che presentino convessità e/o concavità, quale può essere ad esempio la interfaccia poro/matrice in una struttura sinterizzata. Il conteggio si effettua spazzando con un segmento un’area tale da ottenere, in ogni osservazione, un certo numero di conteggi. Si contano le volte che il segmento esplorante diventa tangente ai contorni della fase prescelta che presenti una convessità o una concavità a cui si assegnano, per convenzione valori positivi e negativi. Il conteggio netto, dato dalla differenza tra i due valori, sarà dotato di un segno che è indice di prevalenza.
4. Conteggio dei punti tripli (PA)
Sono detti punti tripli le intersezioni sul piano di lucidatura di caratteristiche lineari; l’attendibilità del numero ottenuto dal conteggio diminuisce con la difficoltà di attuazione.
5. Conteggio di figure (NA)
Alcuni sistemi presentano componenti dispersi nella matrice, tipici esempi sono costituiti da ghise nodulari, acciai a carburi speciali. Può allora essere utile contare il numero di dispersoidi per unità di area come dato complementare della frazione di volume, per la valutazione del volume medio del dispersoide.
Misure di linee possono consistere nella misura delle intercette (LL ), cioè nella misura della parte di segmenti di prova che cade in una certa fase; tale misura può però essere comodamente sostituita da una analisi di punto.
Misure di aree si possono identificare nella misura dell’area relativa occupata da una certa fase (AA), detta misura può essere effettuata su di una immagine della sezione, planimetrando tutte le aree occupate dal componente prescelto. Come nel caso precedente questa misura può essere sostituita da una analisi di punto.
Le misure di volume non rientrano nel campo della stereologia.

Le operazioni, tutte di uguale importanza, che devono essere effettuate per eseguire una analisi di immagine quantitativa di una sezione metallografica sono:
• Preparazione dei campioni;
• Acquisizione delle immagini;
• Trasformazione delle immagini;
• Misura delle grandezze stereologiche di interesse ed analisi statistica.
Preparazione dei campioni
La preparazione dei campioni metallografici per una analisi quantitativa di immagine segue l’identica procedura già vista per la preparazione di campioni metallografici di leghe ferrose e non secondo normativa UNI.
Acquisizione delle immagini mediante digitalizzazione.
Sono attualmente disponibili in commercio a costo contenuto numerosi sistemi computerizzati di acquisizione di immagini da videocamera o da fotocamera con risoluzioni che vanno dal 640 x 480 arrivano a 2560 x 1920 e oltre (i progressi nel settore sono praticamente quotidiani). Si articola in due passi successivi:
• Il campionamento, che consiste nel misurare l’intensità luminosa di ciascuno dei quadratini di una griglia sovrapposta all’immagine (pixel).
• La quantizzazione, che consiste nel convertire i campioni dell’immagine da una rappresentazione analogica continua ad una discreta attraverso i livelli di decisione dk= 2m. Se m=8 ne consegue che dk=256.
Tale acquisizione permette di memorizzare l’immagine su supporto informatico e di procedere alla successiva elaborazione.
Trasformazione delle immagini
Tali trasformazioni sono giustificate dalla necessità di eliminare i difetti (ad esempio elementi estranei alla microstruttura ma presenti sulla superficie del campione) e di evidenziare le zone di interesse dell’analisi. Nei sistemi di elaborazione d’immagine commerciali sono disponibili numerose funzioni di trasformazione (convoluzioni, morfologia matematica, analisi per trasformazione di Fourier, …).
Questa fase è estremamente delicata e richiede notevole esperienza da parte dell’operatore. Il risultato ottenuto deve essere conforme all’obbiettivo desiderato e deve essere ottenuto nel più breve tempo possibile.
L’immagine digitalizzata spazialmente secondo un reticolo di punti quadrato o esagonale, viene sottoposta ad una primissima fase di “pulitura” elettronica, in cui si eliminano gli elementi evidentemente estranei eventualmente presenti, si “binarizza” l’immagine, ottenendo un risultato in cui gli oggetti di interesse sono bianchi “1” ed il fondo è nero “0” (ma si può avere anche il contrario).

Affinché sia possibile modificare l’immagine binarizzata nella morfologia matematica sono utilizzati gli elementi strutturanti. Le trasformazioni a disposizione dell’analista sono numerose e fanno Immagine originale (colori) - Immagine “quantizzata” (256 livelli di grigio) - Immagine binarizzata (bianco e nero). Parte della morfologia matematica: il loro utilizzo è giustificato dalla necessità di eliminare i difetti (per esempio il rumore) e di “precisare” certe zone interessanti per lo studio dell’immagine.
Si dispone di un’ampia gamma di trasformazioni che vanno combinate per segmentare l’immagine e misurare le caratteristiche geometriche richieste. L’analista dovrà fare appello alla sua esperienza: conoscenza degli aspetti delle trasformazioni (trasformazioni di Fourier), scrittura di nuovi algoritmi, ricerca di similitudini con gli studi precedenti. I principali processi d’immagine ausiliari utili ad esempio per l’individuazione di particelle sono: l’erosione dell’area e la dilatazione degli elementi, unitamente a loro combinazioni conosciute con i termini di apertura e chiusura:
Erosione: Rimuove i pixel dal bordo degli oggetti in una immagine binaria. Un pixel è rimosso (commutato a “nero”) se quattro o più dei suoi otto vicini sono neri. L’erosione separa gli oggetti e rimuove i pixel isolati. I valori di quattro ed otto possono essere anche diversamente definiti. Il numero di iterazioni può essere definito (queste due condizioni sono valide per tutte le trasformazioni morfologiche).
Dilatazione: Aggiunge pixel al bordo degli oggetti in una immagine binaria. Un pixel è aggiunto (commutato a “bianco”) se quattro o più dei suoi otto vicini sono bianchi. La dilatazione connette oggetti separati e riempie i fori.
Apertura: Produce una operazione di erosione seguita da una di dilatazione. Arrotonda gli oggetti e rimuove i pixel isolati.
Chiusura: Produce una operazione di dilatazione seguita da una di erosione. Arrotonda gli oggetti e riempie i fori.

Tra le altre operazioni che consentono di modificare l’immagine si ricordano :
Pulitura: è chiamata anche apertura geodetica e fa in modo di erodere gli oggetti di piccole dimensioni senza alterare il resto dell’immagine. I rimanenti oggetti erosi sono quindi ricostruiti nella loro forma originale.
Riempimento di vuoti: questa funzione riempie i vuoti interni all’immagine. Ciò è utile quando si deve individuare soltanto il contorno di un oggetto; in genere infatti dopo la sua applicazione i contorni sono trasformati in aree chiuse.

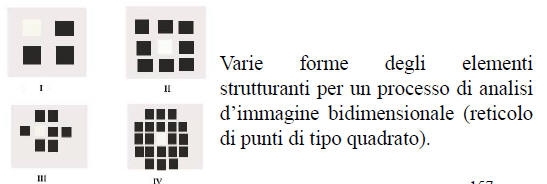
Nel caso in cui si utilizzi un reticolo di punti di tipo quadrato la matrice (o elemento strutturante) utilizzata potrà avere diverse forme, e tutte le funzioni (erosione, dilatazione…) saranno definite dalle matrici e dai numeri di iterazione.
Spesso in metallografia è richiesta la conoscenza di varie grandezze come ad esempio:
•· il numero di particelle o pori su unità di volume
•· le dimensioni dei componenti presenti nel provino
•· le dimensioni dei grani del materiale
•· la frazione di volume delle fasi presenti nel provino, ecc.
per la determinazione dei quali possono essere utilizzati vari metodi.
Per indagini di serie il metodo più veloce è quello di confrontare la superficie del provino (o sue micrografie), con mappe di riferimento standardizzate pubblicate dalle norme.
Tuttavia il metodo che generalmente viene utilizzato per la determinazione quantitativa delle suddette grandezze, è un metodo statistico, attraverso il quale è possibile trarre da poche rilevazioni i valori medi delle grandezze che si vogliono determinare.
Tutte le misure possono essere effettuate sia sulla immagine virtuale nel microscopio, sia sulle micrografie del provino. I valori ottenuti possono essere quindi, distribuiti in classi e tabellati, oppure essere usati in una curva di distribuzione.
Abitualmente i valori misurati in differenti classi, ed il numero dei valori individuati appartenenti a ciascuna classe sono tabellati, e, da essi si ottiene una “curva di frequenza”. Effettuando questi raggruppamenti, i valori misurati vengono distribuiti in classi dimensionali aventi un certo intervallo; esso può essere costante, nel qual caso si ottiene una scala basata su classificazione aritmetica, o, seguire una serie geometrica, in cui ciascun intervallo è ottenuto, moltiplicando il precedente per un fattore costante Praticamente, quando si raggruppano grani o particelle in classi (di area, di diametro, ecc) conviene moltiplicare per fattore (per esempio 2), cosicché ogni classe è multipla dell’altra.
Con i valori misurati, classificati in questo modo, è possibile tracciare un “istogramma od un “poligono di frequenza”. Un istogramma presenta le seguenti caratteristiche:
• esso è costituito da una serie di rettangoli le cui basi sono riportate sulle ascisse e definiscono una precisa classe di appartenenza.
• l’area del rettangolo è la “frequenza” osservata.
• i centri sono punti distintivi della classe, congiungendo i quali si ottiene il poligono di frequenza.
• l’area sottesa al poligono è la “frequenza complessiva”.
La forma del diagramma è fortemente influenzata dalla classificazione scelta. Gli intervalli delle classi debbono essere sufficientemente stretti in modo che nessun dettaglio della curva scompaia, come ad esempio un doppio massimo. Quanto più piccoli sono gli intervalli tanto più il grafico approssima una curva continua, la cosiddetta “ curva di frequenza”.
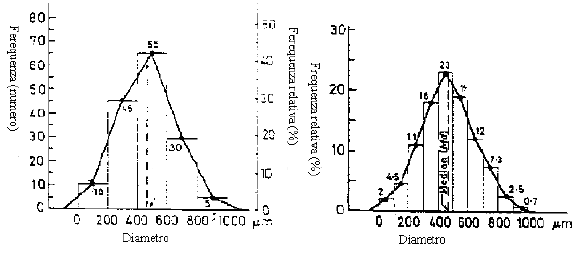
Istogramma e poligono di frequenza per classi dimensionali ad intervallo costante (due differenti intervalli).
La curva di frequenza è caratterizzata dalla moda, cioè dal valore della distribuzione che si manifesta con la massima frequenza, e dalla mediana, cioè quel punto sull’ascissa attraverso il quale è possibile tracciare una linea che divida la superficie sotto la curva in due parti uguali.
Se la distribuzione è simmetrica allora la media aritmetica, con scala lineare, e la media geometrica, con scala logaritmica, coincidono con la mediana.
Una caratteristica della curva di frequenza è la larghezza che costituisce una misura della dispersione del valore misurato attorno alla media.
Si definisce scarto quadratico medio o deviazione standard, la media quadratica degli scarti dei dati intorno al valore medio. Il quadrato dello scarto quadratico medio si chiama varianza e viene spesso usata anche direttamente come misura della variabilità.
La deviazione standard è così espressa :

Quando si usa una classificazione logaritmica (loga), la deviazione standard della distribuzione logaritmica espressa per unità di classe è:
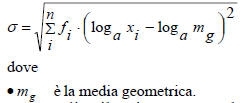
Per una distribuzione normale il 68.27% dei valori misurati è compreso tra ma-s ed ma+ s , cioè ,una deviazione standard per ogni lato della media.
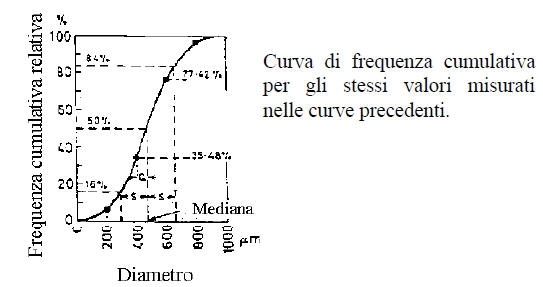
E’ possibile rilevare la differenza nella costruzione delle due curve: nell’istogramma e nel poligono di frequenza normale, la frequenza si individua nel valore centrale della classe, mentre nella curva cumulativa la frequenza è indicata dall’estremo superiore della classe . Per la curva cumulativa, la mediana è l’ascissa del punto cui corrisponde il 50% dell’ordinata. Tuttavia la curva di frequenza fornisce una più chiara descrizione della natura della distribuzione, perciò solitamente vengono tracciate entrambe.
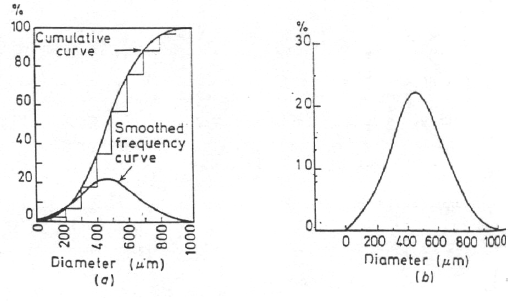
L’obbiettivo della frattografia è quello di analizzare la morfologia di frattura e di tentare di correlare la topografia della frattura alle cause e/o ai meccanismi di base della frattura.

Morfologia duttile (coppa e cono) Morfologia fragile (clivaggio).
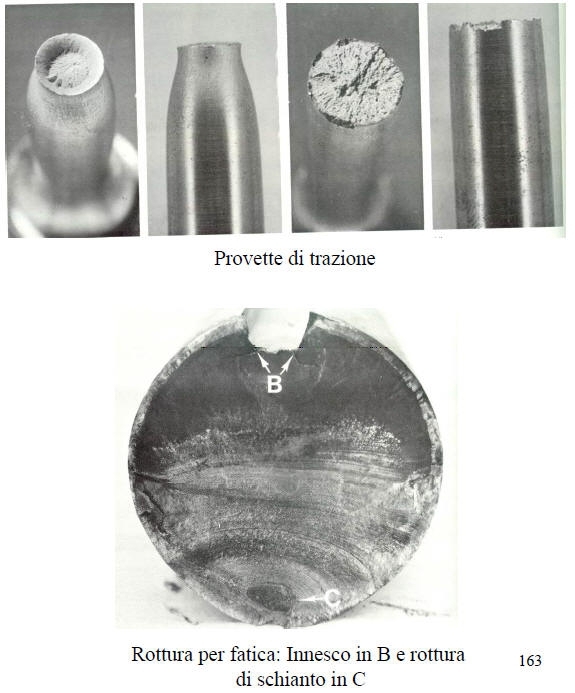
La frattura nelle leghe di interesse industriale può avvenire in modo transgranulare oppure intergranulare. In ogni caso, indipendentemente dal tipo di frattura, esistono essenzialmente 4 tipi di frattura:
• rottura per formazione di dimple
• clivaggio
• fatica
• rottura per decoesione
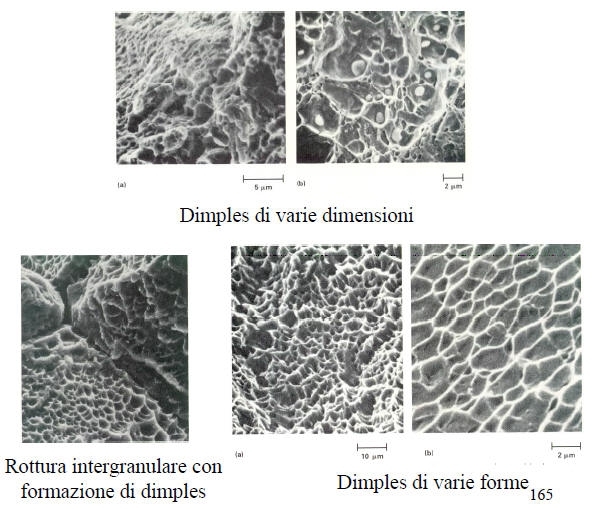
Nel caso in cui il sovraccarico sia la principale causa della frattura, la maggior parte delle leghe commerciali si rompe per coalescenza di microvuoti. Questi microvuoti nucleano in corrispondenza di quelle zone in corrispondenza delle quali si ha una discontinuità nella deformazione localizzata (particelle di una fase secondaria, inclusioni, bordi grano…). In corrispondenza di un aumento della deformazione, i microvuoti crescono, coalescono e formano una superficie continua. La superficie di frattura mostra delle piccole “tazze rovesciate”, appunto dette dimple.
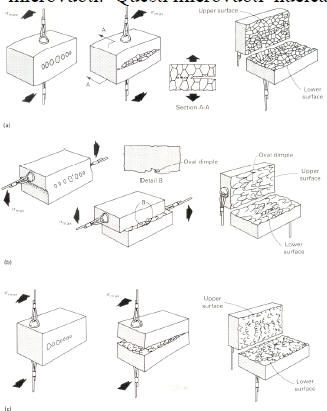
Influenza della direzione di applicazione del carico sulla forma dei dimple, formatisi per coalescenza di microvuoti.
La dimensione dei dimple sulla superficie è governata dal numero e dalla distribuzione dei microvuoti che hanno nucleato. La densità e la distribuzione dei microvuoti giocano un ruolo essenziale nella dimensione e nella distribuzione dei dimple. Se questi nucleano in corrispondenza dei bordi grano, si otterrà una rottura intergranulare per formazione di dimple.
La forma dei dimple dipende dallo stato di sollecitazione presente nel materiale. Dalla figura precedente (a), ad esempio, si può osservare che la frattura nel caso di sollecitazione a trazione monodirezionale.
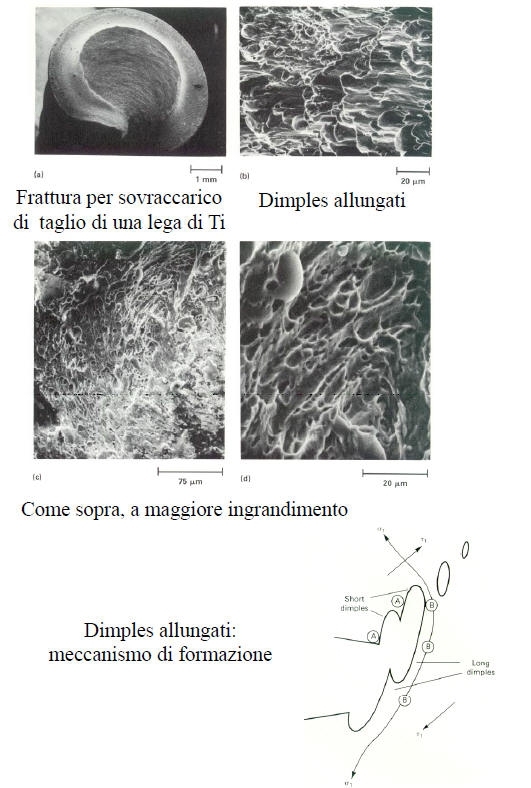
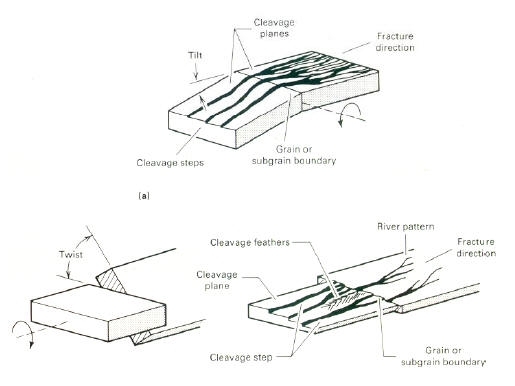
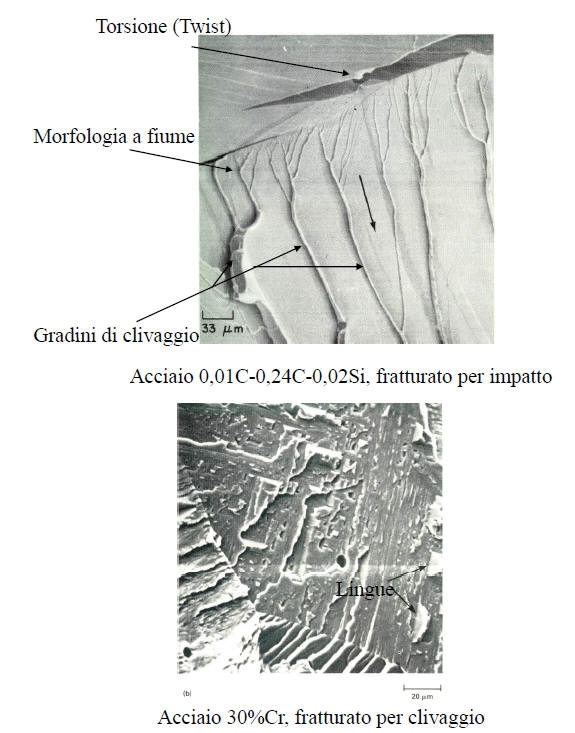
E’ una modalità di frattura a bassa energia (con deformazione plastica praticamente trascurabile) che propaga lungo ben definiti piani cristallografici a basso indice, noti come piani di clivaggio.
Teoricamente, dopo una frattura per clivaggio sarebbe possibile ricostruire perfettamente il manufatto facendo semplicemente ricombaciare i frammenti. Ciò è reso praticamente impossibile per la presenza di imperfezioni nel metallo, quali struttura policristallina, inclusioni, dislocazioni ed altre. Questo implica differenti forme con le quali la frattura per clivaggio si può presentare, quali ad esempio i gradini di clivaggio, morfologia “a fiume” (river pattern), morfologia “a piuma” (feather marking), a “zig zag” (chevron), a “lingua” (tongue).

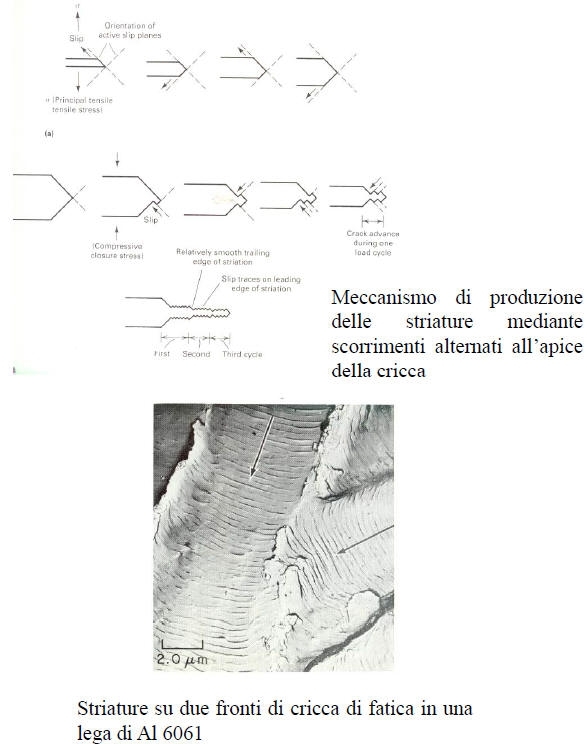
Questa frattura si ha a seguito dell’applicazione di una sollecitazione ripetitiva (ciclica o meno). Essa normalmente si struttura in tre fasi:
• innesco;
• propagazione;
• rottura catastrofica.
Nel diagramma da/dN-DK queste tre fasi corrispondono a tre differenti intervalli di DK applicato.
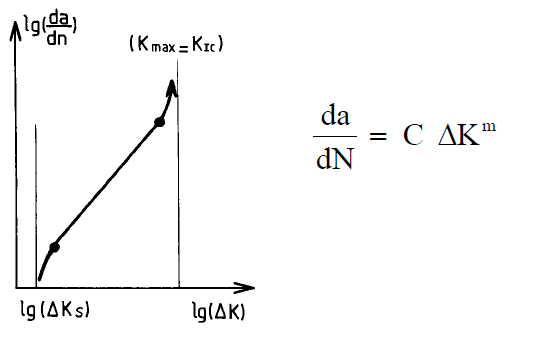
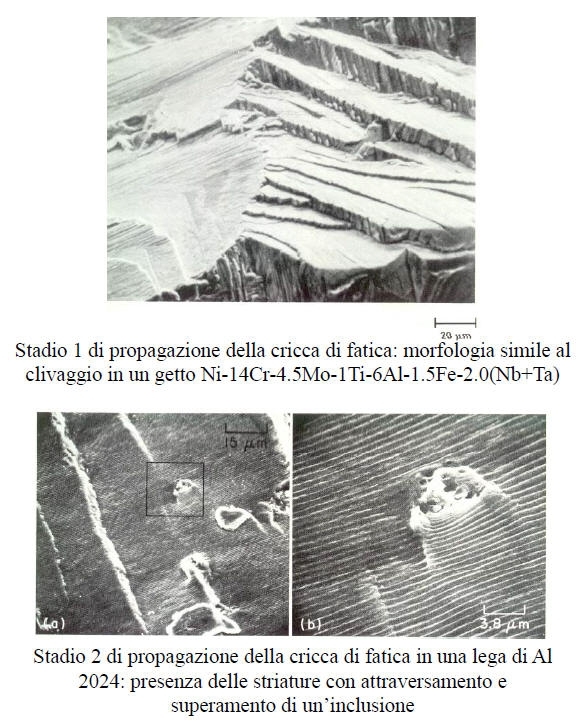
Nello stadio 1 le superfici di frattura sono sfaccettate, spesso simili al clivaggio.
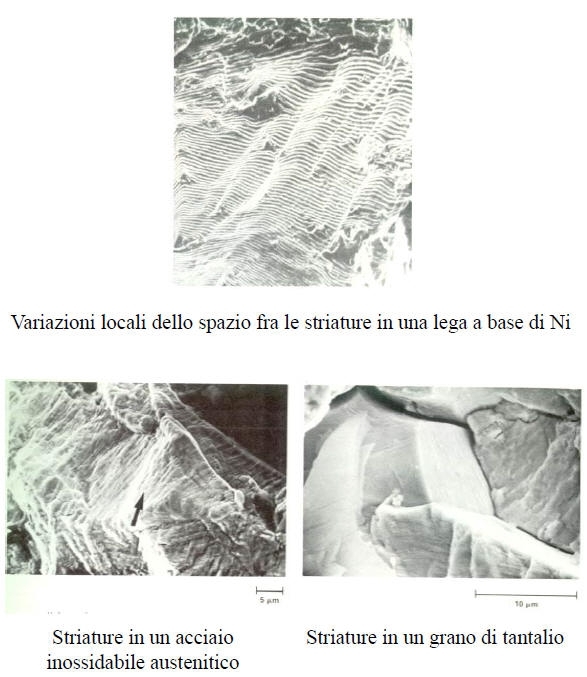
Nello stadio 2 la propagazione avviene solitamente in modo transcristallino e spesso mostra dei segni di arresto della propagazione della cricca detti “linee di fatica” o “striature”.
Nello stadio 3 si ha la rottura di schianto, con la morfologia tipica dei casi di sovraccarico, duttile o fragile a seconda della lega
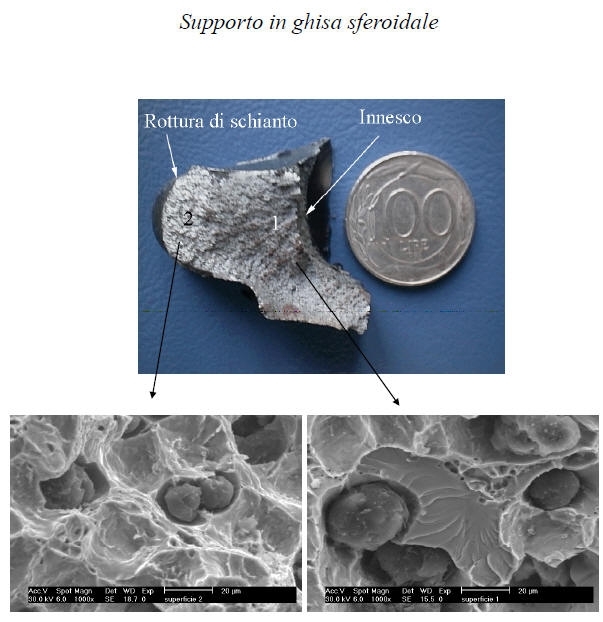
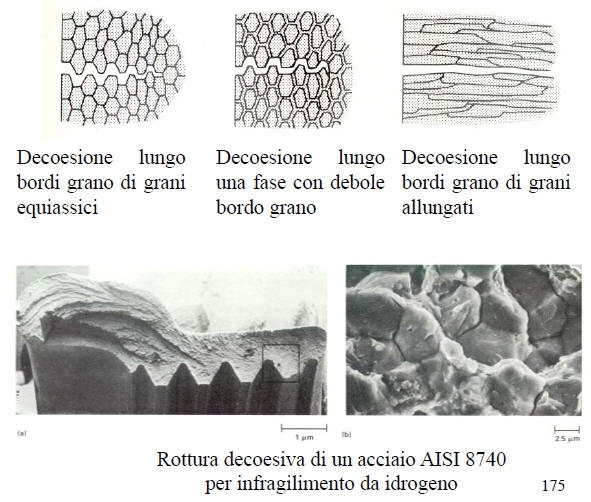
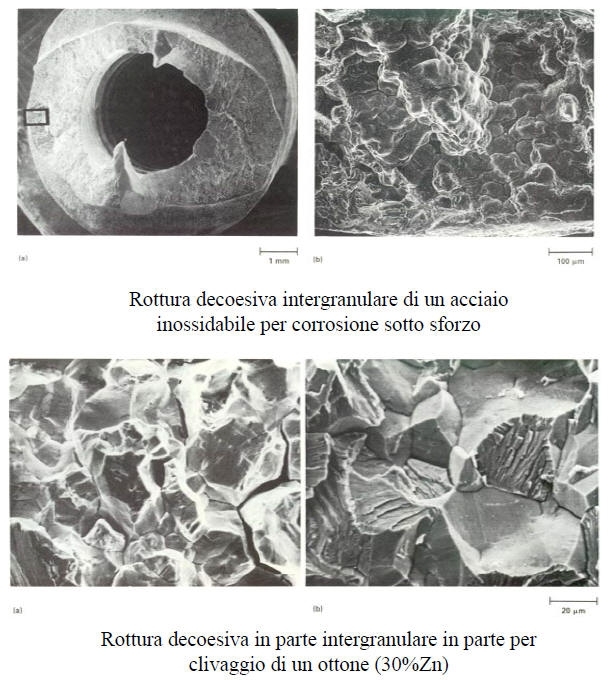
Tale frattura si ha qualora la frattura non mostra deformazione plastica evidente (anche a scala microscopica) e non avviene mediante formazione di dimple, clivaggio o fatica. E’ solitamente dovuta alla presenza di un ambiente aggressivo oppure ad una struttura monofasica ed è associtata ad una frattura intercristallina.
Essa può essere dovuta a numerosi processi, quali ad esempio l’indebolimento dei legami atomici (per adsorbimento di elementi estranei alla lega), rottura di film protettivi, dissoluzione anodica….
Portale "Ingegneria e
Campanologia" -
Autore -
Sommario
- Mappa del Sito -
Home
Bib-TS-010 - M. Cavallini, F. Iacoviello - Materiali Metallici - Francesco Ciolfi Editore, via E. De Nicola, Cassino
Bib-TS-011 - W. Nicodemi - Metallurgia - Masson, Milano
Bib-TS-012 - A. Cigada - Struttura e proprietà dei materiali metallici - Città Studi, Milano
Bib-TS-013 - Lucidi del corso di "Metallurgia" sono disponibili in formato pdf all’indirizzo: http://www.metallurgia.unicas.it