Portale "Ingegneria e Campanologia" - Autore - Sommario - Mappa del Sito - Home
Meccanica del mezzo continuo e dei
materiali
AREA I - ARTE TECNICO-SCIENTIFICA (ATS)
Cap. ATS-H01 - Meccanica - Pag. ATS-H01.05
Gli argomenti trattati sono stati inseriti da Ing. Arch. Michele Cuzzoni nel 2012 - © Copyright 2007- 2025- e sono desunti dalla documentazione indicata in Bibliografia a fondo pagina
Si consideri un provino di materiale omogeneo e isotropo, di spessore infinito nella direzione perpendicolare allo schermo, a cui è applicato uno sforzo di trazione (Fig. H01-05-A). La frattura si può definire come numero scalare: sia σ il valore della componente del tensore degli sforzi che descrive la trazione in direzione verticale.
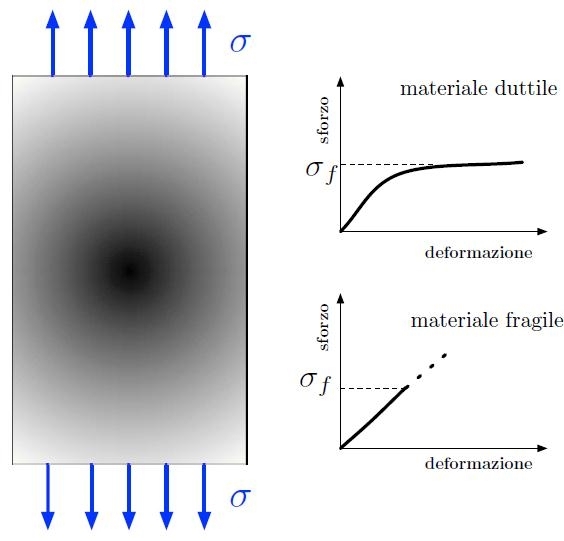
Figura H01-05-A:
Sinistra: provino di materiale omogeneo e isotropo; σ è la componente dello sforzo che definisce la trazione lungo la verticale.
Destra (alto): curva sforzo deformazione per un materiale duttile. Destra (basso): curva sforzo-deformazione per un materiale fragile.
Il valore σf rappresenta lo sforzo di snervamento (materiali duttili) o di cedimento (materiali fragili).
A seconda del tipo di reazione allo sforzo esterno (Fig. H01-05-A) i materiali possono essere:
-
Duttili: reazione elastico lineare per piccoli sforzi; deformazioni permanenti irreversibili per grossi sforzi (comportamento plastico, tipico dei metalli). Un materiale duttile può sostenere grandi deformazioni senza rompersi per forza. Questa proprietà è caratteristica dei materiali che hanno dislocazioni nel reticolo. La curva di sforzo-deformazione dei materiali duttili è in Fig. H01-05-A a destra in alto. Se σ > σf , il materiale duttile cede. Questa condizione è detta limite di snervamento.
-
Fragili: la reazione di risposta è lineare solo fino a un certo valore di sforzo chiamato sforzo di cedimento oltre al quale si rompono in modo irreversibile. Per i valori σ > σf non si può rappresentare la curva sforzo deformazione. Questo aspetto è chiamato frattura fragile ed è tipico dei materiali ceramici, dei semi conduttori, del vetro. Dopo l'innesco della frattura, se ne ha propagazione irreversibile.
Il provino di Fig. H01-05-A funziona assumendo che esso sia un continuo perfetto, cioè un sistema privo di microstruttura. Sotto questo aspetto la microstruttura di un mezzo materiale non c'entra con la sua composizione atomica; quanto detto si riferisce infatti alla teoria del continuo. Il concetto di "assenza di microstruttura" significa che nella matrice continua si ha assenza di difetti (es. disomogeneità, inclusioni, vuoti) oppure si hanno fessure (dette anche cricche).
E' tuttavia possibile avere dei cedimenti anche utilizzando valori di σ molto inferiori a σf. Per conciliare le varie ipotesi è necessario constatare che ogni oggetto a livello microscopico è complesso. Cioè il materiale non è omogeneo ed isotropo, contenente eventuali disomogeneità: regioni con proprietà elastiche diverse o con fessure vuote, il tutto immerso in una matrice uniforme. L'esistenza della microstruttura cambia l'analisi della frattura. Si veda come esempio la fig. H01-05-B costituita da un materiale disomogeneo che ha all'interno una micro-fessura.
Considerando la fig. H01-05-B, si può dimostrare che una fessura ellittica agisce come un concentratore di sforzo. Su ognuno degli apici di cricca lo sforzo risultante σtip è dato da:
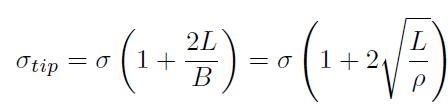 [H01-05-01]
[H01-05-01]
dove:
σ = sforzo applicato
σ = B2/ L è il raggio di curvatura dell'apice della cricca. Questo è il criterio di Inglis (1913): un materiale reale cede a valori di sforzo applicato inferiore al valore di cedimento teorico, dove teorico vuol dire un materiale continuo privo di microstruttura. Può succedere che uno sforzo applicato σ < σf localmente sia ampliato oltre il limite di cedimento e generare quindi la propagazione di una micro fessura.
Ecco due casi particolari:
-
cricca di eccentricità nulla: posto B = L e σtip/σ = 3. Equivale a dire che un foro circolare riduce la resistenza a frattura di un mezzo fragile di un fattore tre. A parità di sforzo applicato, indica che con la presenza di un foro circolare il fattore di intensificazione di sforzo è pari a 3 e quindi lo sforzo di cedimento è ridotto di 1/3.
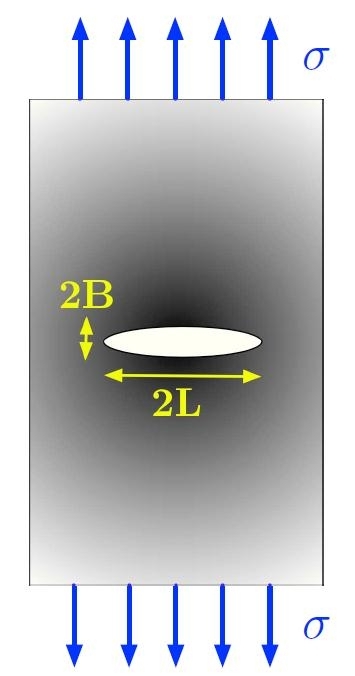
Figura H01-05-B:
Sistema continuo ed isotropo contenente una cricca ellittica di asse maggiore 2L ed asse minore 2B, posta trasversalmente all’asse di carico.
Caso bidimensionale (corrispondente ad un sistema reale di spessore molto grande e contenente una cricca passante).
-
cricca sottile: in questo caso L >> B e quindi
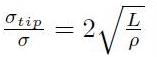 [H01-05-02]
[H01-05-02]
Si definisce fattore di intensificazione di sforzo l'espressione delineata nell'equazione [H01-05-02], che dipende da fattori geometrici: la dimensione L della fessura e la sua forma data dal valore della curvatura σ al suo apice. Il modello di Inglis indica che a parità di materiale, forma di cricca e condizioni di carico, maggiore è la dimensione della fessura e minore è la resistenza a frattura.
In caso di cricca sottile, si consideri il limite di fessura infinitesimamente sottile per cui σ ® 02: lo sforzo all'apice di fessura diverge.
Non esiste un materiale reale che può resistere a questo sforzo. Pertanto, secondo il modello di Inglis, un materiale che contiene una fessura sottilissima può rompersi per applicazione di uno sforzo comunque piccolo (nel caso ideale, anche infinitesimo). Tuttavia la fisica sperimentale dimostra che materiali fessurati, sotto particolari condizioni, riescono a resistere alla frattura.
La frattura fragile avviene quando il materiale raggiunge il limite di cedimento ed esso si rompe in maniera irreversibile.
Secondo la fisica sperimentale, per consentire la propagazione di una cricca occorre che l'attuazione dell'evento sia energeticamente favorevole. L'energia elastica accumulata dal materiale (come conseguenza del campo di forze di trazione) deve essere sufficiente alla creazione di due nuove superfici libere interne che si formano man mano che la cricca avanza.
In Fig. H01-05-C si osserva una fessura di lunghezza 2L, all'interno di un materiale (oppure mezzo omogeneo e isotropo) lineare elastico, essa può avanzare per effetto di uno sforzo di trazione σ esclusivamente se la variazione di energia totale dEt per aumento elementare della lunghezza dL è negativo. Cioè l'enunciato del Criterio di Griffith si scrive così:
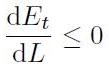 [H01-05-03]
[H01-05-03]
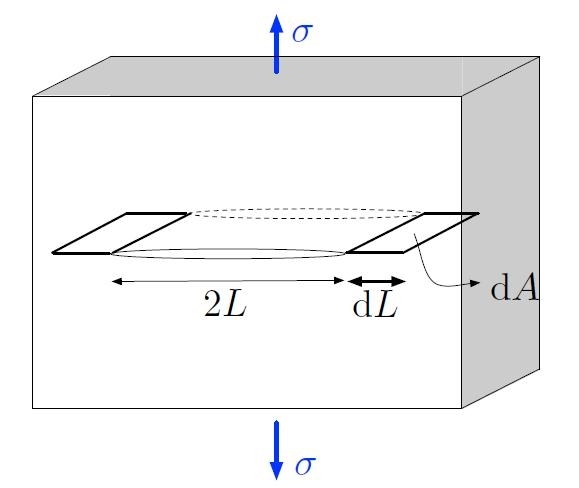
Figura H01-05-C:
Il Criterio di Griffith: una fessura ellittica di lunghezza 2L subisce un incremento di lunghezza 2dL per effetto della trazione σ.
Contemporaneamente, l’area della superficie interna del materiale aumenta di una quantità 2dA.
In questo ambiente Et diventa una energia libera di Helmholtz e quindi il processo fisico progredisce solo se essa diminuisce. Man mano che la fessura avanza, si crea nuova superficie interna della dimensione di dA per ogni allungamento dL della fessura.
Il sistema di energia totale Et è uguale alla somma di un'Energia di superficie Es e di un aumento di energia meccanica di interazione Wi :
Et = Es + Wi [H01-05-04]
dove:
Es = lavoro necessario per creare la nuova superficie - fattore legato alla struttura atomica del materiale ed al tipo di legami chimici al suo interno.
Wi = è l'energia di interazione che descrive la relazione esistente tra il lavoro compiuto dalle forze che creano lo stato di carico del mezzo e l'energia potenziale elastica accumulata in esso.
Anche l'energia di interazione si può scrivere come somma di due valori:
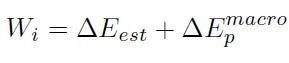 [H01-05-05]
[H01-05-05]
dove:
ΔEest = differenza di lavoro che le forze esterne agenti sul sistema devono esercitare nei casi opposti di mezzo fessurato e mezzo ideale.
ΔEpmacro = differenza di energia potenziale elastica nel mezzo, tra il caso in cui la fessura è presente e quello in cui è assente.
Se si pone che lo sforzo applicato σ sia costante mentre la frattura si apre, si può dimostrare che:
ΔEest = - 2 ΔEpmacro
in modo che:
Wi = - ΔEpmacro [H01-05-06]
Il segno negativo dell'energia meccanica indica una riduzione reale di energia durante la propagazione della fessura. L'equazione [H01-05-03] si può così scrivere:
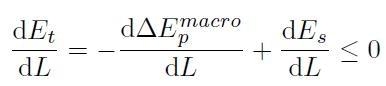 [H01-05-07]
[H01-05-07]
Esplicitando si ottiene:
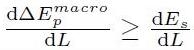 [H01-05-08]
[H01-05-08]
Quest'espressione afferma che per avere una frattura in un materiale, occorre che la variazione di energia potenziale elastica dovuta alla presenza della fessura, sia superiore al lavoro fatto per creare nuova superficie libera interna.
L'energia di superficie Es espressa per larghezza unitaria del fronte di frattura, si può esprimere come:
Es = 4 L γs [H01-05-09]
Dove:
γs = energia per larghezza unitaria di fronte di frattura spesa per generare un incremento unitario della lunghezza di fessura.
Se si osserva la Fig. H01-05-C, il fronte si sviluppa ortogonalmente sia all'asse di carico, sia all'asse di fessura. L'energia γs è un parametro tipico del materiale: misura il lavoro necessario a rompere i legami chimici - che tengono coeso il materiale - lungo la linea ideale che rappresenta un segmento unitario del fronte di frattura. Il valore di γs è un parametro del materiale.
Per il Criterio di Griffith l'equazione [H01-05-08], si può scrivere così (considerando un mezzo lineare elastico di modulo di Young E e Coefficiente di Poisson ν, soggetto a deformazione di apertura):
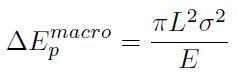 [H01-05-10]
[H01-05-10]
La condizione fisica di propagazione della fessura è tale che lo sforzo σ applicato normalmente all'asse maggiore della fessura soddisfi la condizione:
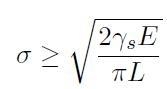 [H01-05-11]
[H01-05-11]
Si definisce allora sforzo di cedimento σf per una cricca di lunghezza Lf l'espressione:
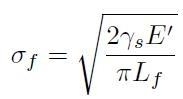 [H01-05-12]
[H01-05-12]
Per ogni cricca di lunghezza assegnata
Lf esiste un valore di sforzo applicato oltre a cui il
materiale cede (cioè la fessura si propaga); fissato un valore di sforzo
tensile
![]() si propagheranno tutte le fessure presenti nel materiale, purché la loro
semilunghezza iniziale sia uguale o superiore alla lunghezza critica Lf:
si propagheranno tutte le fessure presenti nel materiale, purché la loro
semilunghezza iniziale sia uguale o superiore alla lunghezza critica Lf:
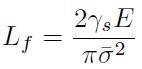 [H01-05-13]
[H01-05-13]
Il Criterio di Griffith si può applicare anche oltre il limite di comportamento fragile; per applicare l'equazione anche a materiali duttili, si introduce il concetto di lavoro plastico (p) - che rappresenta l'energia spesa dalle forze di carico per generare una deformazione permanente nel sistema - per ogni elemento di superficie e per una larghezza unitaria del fronte di frattura. Allora lo sforzo di snervamento in un materiale duttile è dato da:
La teoria di Griffith è estremamente semplice dal punto di vista concettuale e conduce a risultati quantitativamente corretti e, soprattutto, espressi come funzione di parametri materiali calcolabili o misurabili direttamente. Essa riveste un ruolo di paradigmantica importanza concettuale nella meccanica della frattura ed è stata applicata anche oltre il limite di comportamento fragile. Ciò è fattibile, a livello elementare, introducendo una semplice correzione fenomenologica che renda tale equazione applicabile anche a materiali duttili.
Si indichi con p il lavoro plastico (questo lavoro rappresenta l’energia spesa dalle forze di carico per generare una deformazione permanente nel sistema) per elemento di superficie (e per una larghezza unitaria di fronte di frattura). Allora è possibile proporre una formula fenomenologica per lo sforzo di snervamento in un materiale duttile come segue
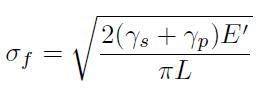 [H01-05-14]
[H01-05-14]
Si introduca la forza generalizzata G di propagazione della frattura, che rappresenta l'energia disponibile per ogni incremento dL della lunghezza della fessura per una larghezza unitaria del fronte di frattura:
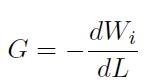 [H01-05-15]
[H01-05-15]
Dalle equazioni [H01-05-06] e [H01-05-10] si ricava:
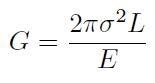 [H01-05-16]
[H01-05-16]
Applicando lo sforzo di cedimento σf dell'equazione [H01-05-12], si può formulare il criterio di Griffith nella forma: la condizione fisica a partire da cui si osserva la propagazione della cricca è la forza generalizzata di propagazione della frattura che raggiunge il valore critico Gc dato da:
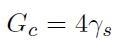 [H01-05-17]
[H01-05-17]
Ogni materiale ha un proprio valore di Gc.
Si introduce ora il parametro di Resistenza alla frattura R applicato all'energia di superficie Es, che misura il lavoro che si deve fare per ogni incremento dL della lunghezza della fessura e per la larghezza unitaria del fronte di frattura (Fig. H01-05-C).
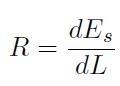 [H01-05-18]
[H01-05-18]
Il parametro R varia da materiale a materiale: designa il lavoro che occorre realizzare sul sistema, per rompere una sequenza di legami chimici attraverso il fronte di frattura, per far avanzare il fronte di frattura stesso. Tale lavoro dipende dalla densità spaziale dei legami (orientamento cricca rispetto alla cristallografia del mezzo), dalla loro natura e forza.
R e G sono necessari per esprimere il bilancio energetico scritto nell'equazione [H01-05-04]. Per ogni processo di avanzamento dL vale la relazione:
![]() [H01-05-19]
[H01-05-19]
Quando vale il caso G = Gc si ha che la resistenza a frattura è data dall'energia di superficie:
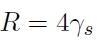 [H01-05-20]
[H01-05-20]
Il fronte di frattura avanza se G > R, mentre regredisce se G < R. Nella tabella [H01-05-a] si possono leggere i valori di resistenza a frattura (prima colonna), di forza generalizzata critica Gc (seconda colonna) per vari materiali fragili reali.
Considerando le equazioni [H01-05-17] e [H01-05-20], la differenza tra i valori delle grandezze riportate in prima e seconda colonna fornisce una stima della deviazione di ciascun materiale dal comportamento fragile ideale.

Tabella [H01-05-a]:
Valori della resistenza a frattura R, dell’energia di superficie 4 γs e della tenacità a frattura KI,c per diversi materiali fragili reali.
Si consideri il provino di Figura H01-05-B, considerando il modello di Inglis per cui la cricca funziona come concentratore di sforzo, si calcoli ora il campo di sforzo Ť in un intorno dell'apice della cricca.
Si considerino le componenti associate alla direzione dell'asse di cricca, denominato x, e quella della direzione di carico detta y. Il problema bidimensionale definisce per ogni punto P il valore locale delle tre componenti indipendenti Txx, Tyy e Txy come indicato in Figura H01-05-D.
Attorno a P si delinea un elemento infinitesimo quadrato; sia Txy = Tyx per la simmetria del tensore degli sforzi. L'origine degli assi è posta al centro della fessura. Introdotte le coordinate polari (r, ρ) centrate sull'apice della cricca, per designare la posizione di P sul piano x-y.
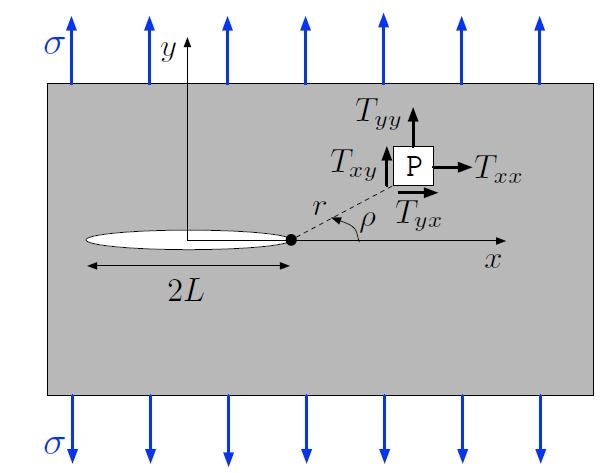
Figura H01-05-D:
Componenti Txx, Tyy e Txy = Tyx del tensore degli sforzi nel punto P posto nell’apice di una cricca di lunghezza 2L. Al sistema è applicata la trazione σ.
Si può dimostrare che:
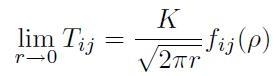 [H01-05-21]
[H01-05-21]
dove i, j = x, y. Così:
-
la funzione fij(ρ) rappresenta un fattore geometrico;
-
K è il fattore di intensificazione dello sforzo ed è legato alla forza generalizzata per la propagazione di frattura dalla relazione:
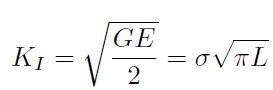 [H01-05-21]
[H01-05-21]
Allora per il Criterio di Griffith, posto G = Gc si ha:
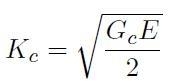 [H01-05-22]
[H01-05-22]
dove Kc è la tenacità a frattura. Il valore di questo parametro per diversi materiali è riportato in Tabella [H01-05-b], da cui si ricava che maggiore è il valore di Kc e maggiore è la resistenza meccanica del materiale.
Portale "Ingegneria e
Campanologia" -
Autore -
Sommario
- Mappa del Sito -
Home
Bib-TS-147 - Michele Cuzzoni, Appunti di Scienza
delle Costruzioni - Università degli Studi di Pavia - Facoltà di Ingegneria -
AA. 1995 - 1996
Bib-TS-148 - Michele Cuzzoni, Appunti di Tecnica delle Costruzioni -
Università degli Studi di Pavia - Facoltà di Ingegneria - AA. 1996 - 1997.