Portale "Ingegneria e Campanologia" - Autore - Sommario - Mappa del Sito - Home
Meccanica del mezzo continuo e dei
materiali
AREA I - ARTE TECNICO-SCIENTIFICA (ATS)
Cap. ATS-H01 - Meccanica - Pag. ATS-H01.04
Gli argomenti trattati sono stati inseriti da Ing. Arch. Michele Cuzzoni nel 2012 - © Copyright 2007- 2025- e sono desunti dalla documentazione indicata in Bibliografia a fondo pagina
Una forza conservativa si calcola dal gradiente della funzione energia potenziale associata al campo di forze conservative. Nel caso di mezzo continuo elastico che si trova a temperatura nulla, esiste la funzione energia potenziale elastica. Indicato con U il valore dell'energia potenziale elastica per unità di volume, si può generalizzare la relazione forza - potenziale della meccanica al caso in cui la forza corrisponde al campo di sforzo Tij presente nel mezzo e il gradiente di U è calcolato rispetto al campo di deformazione Єij. Si ha:
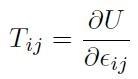 [H01-04-01]
[H01-04-01]
L'equazione [H01-04-01] afferma che: esiste una densità di energia potenziale elastica da cui è possibile ottenere la relazione costitutiva del mezzo. Considerando un intervallo infinitesimo di tempo dt si può scrivere la seguente equazione che rappresenta l'espressione generale che lega l'energia elastica accumulata nel mezzo nell'unità di tempo, sotto l'effetto di una deformazione variabile nel tempo:
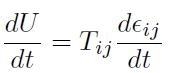 [H01-04-02]
[H01-04-02]
Se il mezzo è lineare (anisotropo), l'equazione si scrive così: Tij = Cijkh Єkh
Da cui si ottiene:
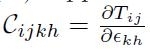
E utilizzando l'equazione [H01-04-01] si ha:
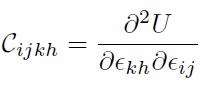 [H01-04-03]
[H01-04-03]
Il tensore elastico ha forma simmetrica nelle coppie di indici (ij) e (kh), poiché la derivata seconda di una funzione regolare è permutabile. Nel caso lineare si può esplicitare la funzione U in forma molto compatta: dalla relazione di equazione [H01-04-02] si ha:
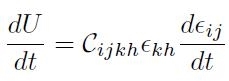 [H01-04-04]
[H01-04-04]
e, sfruttando la proprietà di simmetria si scrive:
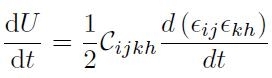 [H01-04-05]
[H01-04-05]
cioè:
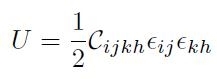 [H01-04-06]
[H01-04-06]
In un mezzo lineare isotropo, diventa (utilizzando i coefficienti di Lamé):
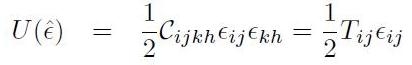
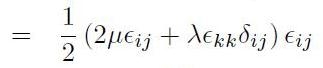
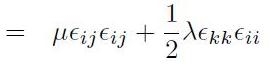 [H01-04-07]
[H01-04-07]
Essendo:
![]() e che
e che
![]() si può scrivere:
si può scrivere:
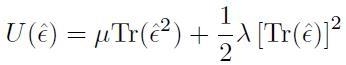 [H01-04-08]
[H01-04-08]
che rappresenta la forma più generale per la dipendenza della densità di energia potenziale elastica dalla deformazione in un mezzo elastico omogeneo ed isotropo per deformazioni a temperatura nulla.
Se le deformazioni avvengono a temperatura finita, si considerano le trasformazioni termodinamiche in regime quasi - statico: la deformazione avviene in tempi sufficientemente lunghi da permettere di considerare il sistema sempre in equilibrio termodinamico istantaneo ad una data temperatura.
Se la temperatura è maggiore di 0, tutti i moti di agitazione termica dei costituenti elementari sono attivi. E' necessario considerare il loro contributo energetico, e il contributo che descrive il passaggio di calore dal mezzo elastico all'ambiente esterno e/o viceversa. Con questo meccanismo il calore viene scambiato con l'esterno esprimendo la seguente equazione:
![]() [H01-04-09]
[H01-04-09]
Dove:
T = temperatura
S = entropia per unità di volume
Q = calore assorbito per unità di volume.
Quindi il primo principio della termodinamica si può scrivere nella seguente forma completa:
![]() [H01-04-10]
[H01-04-10]
Dove:
U = densità di energia interna del sistema in oggetto.
L'equazione [H01-04-10] è l'equazione fondamentale della termodinamica dei mezzi continui deformati quasi - staticamente (reversibilmente).
Con deformazioni particolari l'equazione [H01-04-10] si riconduce ai risultati normali della termodinamica classica. Per esempio si abbia il caso di una deformazione di compressione o espansione, descritta dal tensore degli sforzi del tipo:
![]()
Dove:
P = pressione idrostatica applicata
segno - = la pressione è esercitata sul sistema
Allora si ha:
![]() [H01-04-11]
[H01-04-11]
Se risulta
![]() variazione
di volume per unità di volume. Allora il bilancio energetico per un sistema
compresso idrostaticamente in modo reversibile diventa:
variazione
di volume per unità di volume. Allora il bilancio energetico per un sistema
compresso idrostaticamente in modo reversibile diventa:
![]() [H01-04-12]
[H01-04-12]
In questo caso ogni grandezza estensiva è espressa per unità di volume, mentre temperatura e pressione - che sono grandezze intensive - si misurano nelle unità convenzionali.
Si definisca ora l’energia libera di Helmholtz F (per unità di volume):
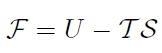 [H01-04-13]
[H01-04-13]
Utilizzando questo potenziale termodinamico si possono scrivere espressioni operative inverse che permettono di calcolare direttamente il tensore degli sforzi:
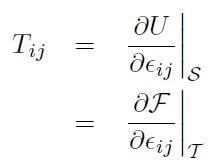 [H01-04-14]
[H01-04-14]
dove si mantengono costanti rispettivamente, l'entropia (I caso) e la temperatura (II caso).
Si considerino:
- un mezzo omogeneo e isotropo in regime di piccole deformazioni reversibili;
- la temperatura T uniforme e costante in tutto il mezzo.
Detta Fo l'energia libera in assenza di deformazioni alla stessa temperatura di quando le deformazioni sono attive.
Si può allora assumere il potenziale F come espandibile in serie di potenze delle deformazioni:
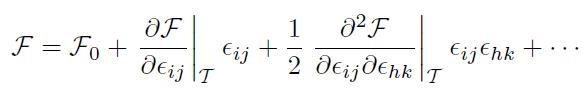 [H01-04-15]
[H01-04-15]
Il termine al primo ordine in Єij deve essere nullo: vale l'equazione [H01-04-14] e all'equilibrio (in assenza di deformazioni) lo sforzo TiJ è nullo.
Quindi i primi termini utili sono quelli quadratici e sono gli unici che si considerano poiché le deformazioni sono piccole.
Visto che il termine F0 è definito a meno di una costante arbitraria, è opportuno porre anche F0 = 0.
Essendo l'energia libera F uno scalare, allora anche il termine quadratico lo sarà.
Poichè il tensore delle piccole deformazioni
![]() è
simmetrico, con i suoi elementi si possono costruire due sole grandezze scalari
indipendenti:
è
simmetrico, con i suoi elementi si possono costruire due sole grandezze scalari
indipendenti:
![]()
Poiché:
![]()
Si può scrivere:
![]() [H01-04-16]
[H01-04-16]
che rappresenta l’espressione generale per l’energia libera di un mezzo omogeneo ed isotropo.
Se si associano le due costanti c1 e c2 ai coefficienti di Lamé secondo le relazioni:
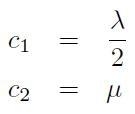 [H01-04-17]
[H01-04-17]
si ha la spiegazione termodinamica del motivo per cui un mezzo omogeneo e isotropo in regime lineare sia caratterizzato da due soli moduli elastici.
L'energia libera intesa come funzione della deformazione permette di dimostrare le condizioni fondamentali che i moduli elastici devono soddisfare.
All'equilibrio F è minima e vale 0 per la deformazione che corrisponde a Єij = 0 per ogni i , j.
Quindi la forma quadratica data in [H01-04-16] è definita positiva.
Il solido elastico in condizione non deformata è in equilibrio stabile per ipotesi e l'energia potenziale relativa ha un minimo in corrispondenza di questa condizione. Posto l'energia potenziale uguale a 0 in condizione non deformata, l'equazione [H01-04-16] è sempre positiva.
Supponendo una deformazione per cui Єij = 0, si ha:
F = c2 Єij Єij > 0
Þ c2 > 0 [H01-04-18]
Applicando la deformazione: Єij = sδij con s Є R si ha:
F = c1 (sδii) (sδjj) + c2 (sδij) (sδij) = 9 s2 c1 + 3 s2 c2 > 0 Þ 3 c1 + c2 > 0 [H01-04-19]
Per l'equazione [H01-04-17] si ricavano:
μ > 0 [H01-04-20]
3λ + 2 μ > 0 [H01-04-21]
Ricordando le corrispondenze tra i 5 moduli elastici di un mezzo omogeneo e isotropo, date dalla tabella seguente:

si dimostrano le seguenti relazioni:
K = (3λ + 2μ) / 3 Þ K > 0 [H01-04-22]
E = ( 9 K μ ) / (3K + μ) Þ E > 0 [H01-04-23 e H01-04-24]
Anche il modulo di Poisson può essere definito in un intervallo assoluto di variabilità: considerando la relazione:
ν = (3K - 2μ) / 2 (3K + μ) [H01-04-25]
si dimostra che:
ν = (3K - 2μ) / 2 (3K + μ) = 1/2 - 3μ / (2(3K + μ) < 1/2 [H01-04-26]
e che:
ν = (3K - 2μ) / 2 (3K + μ) = 9K / (2(3K + μ) - 1 > - 1 [H01-04-27]
Raggruppando le precedenti si ha:
- 1 < ν < 1/2 [H01-04-28]
Questo risultato, che ammette valori negativi per il modulo di Poisson, rivela che esistono materiali non convenzionali per cui il modulo è negativo (mentre nei casi tradizionali ν > 0 per cui essi si restringono trasversalmente se allungati longitudinalmente). Esempi tipici dei materiali speciali sono le schiume, i laminati e alcuni nano-porosi o micro-porosi.
Supponendo variabile la temperatura di un sistema si esaminino i seguenti due casi:
- deformazione indotta da una variazione di temperatura;
- deformazione che produca un riscaldamento o raffreddamento del mezzo.
Quindi l'espressione dell'energia libera deve contenere un termine di accoppiamento temperatura - deformazione.
In regime di piccole deformazioni e assumendo piccole
variazioni di temperatura ΔT è ovvio scrivere il termine di accoppiamento in
modo che dipenda da termini al primo ordine in
![]() e ΔT. Poiché
e ΔT. Poiché
![]() è un tensore simmetrico di rango 2, si può costruire a partire dalle sue
componenti una sola grandezza scalare invariante di primo grado, cioè la sua
traccia.
è un tensore simmetrico di rango 2, si può costruire a partire dalle sue
componenti una sola grandezza scalare invariante di primo grado, cioè la sua
traccia.
Allora l’energia libera per un mezzo omogeneo ed isotropo in condizioni di temperatura variabile vale:
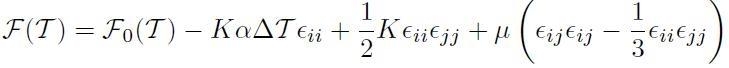 [H01-04-29]
[H01-04-29]
Dove:
F0(T) = contributo di energia libera del sistema indeformato, dipendente solo dalla temperatura.
1/2 K Єii Єjj e μ (Єij Єij - 1/3 Єii Єjj ) descrivono la variazione meccanica (legata alla deformazione) di energia libera e non hanno contributi termodinamici.
- K α ΔT Єii è il termine di accoppiamento.
Il termine degli sforzi in condizioni di temperatura variabile si ricava applicando l'equazione [H01-04-14]:
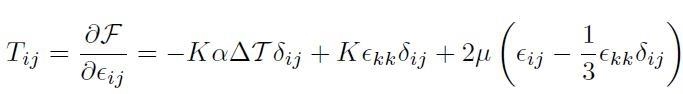 [H01-04-30]
[H01-04-30]
Dove:
- K α ΔT δij è lo sforzo (interno) indotto dalla variazione di temperatura.
Nel caso particolare di dilatazione termica libera, che avviene in assenza di sforzi esterni applicati al sistema, dopo la dilatazione il sistema raggiungerà un nuovo stato di equilibrio in cui gli sforzi interni sono nulli. Si ha quindi:
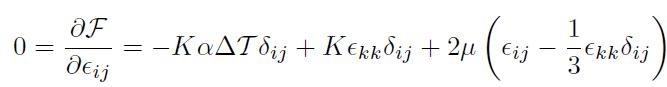 [H01-04-31]
[H01-04-31]
Che diventa:
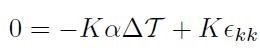 [H01-04-32]
[H01-04-32]
cioè:
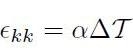 [H01-04-33]
[H01-04-33]
Quindi α è il coefficiente di dilatazione (volumetrica) termica del sistema considerato. Il coefficiente si calcola nel seguente modo:
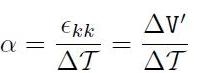 [H01-04-34]
[H01-04-34]
sapendo che:
![]()
è la variazione relativa di volume (per unità di volume)
dell’elemento considerato. Ne segue che α è misurato in K−1 (perché
![]() è adimensionale).
è adimensionale).
In Tabella [H01-04-35] si riportano i valori medi (a temperatura ambiente) di α per alcuni materiali.
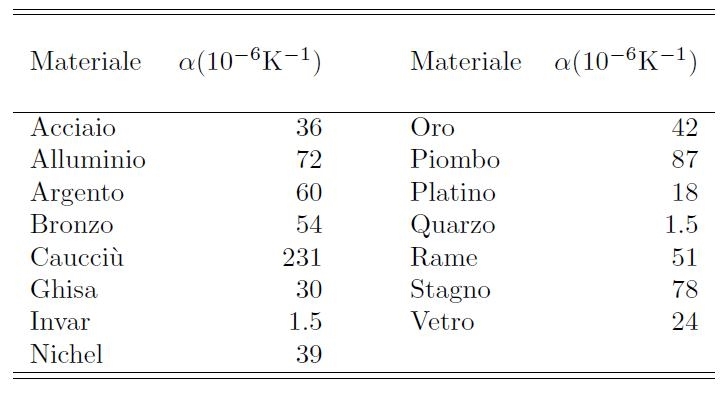
Tabella [H01-04-35]: Valori medi della costante di alcuni materiali.
Portale "Ingegneria e
Campanologia" -
Autore -
Sommario
- Mappa del Sito -
Home
Bib-TS-147 - Michele Cuzzoni, Appunti di Scienza
delle Costruzioni - Università degli Studi di Pavia - Facoltà di Ingegneria -
AA. 1995 - 1996
Bib-TS-148 - Michele Cuzzoni, Appunti di Tecnica delle Costruzioni -
Università degli Studi di Pavia - Facoltà di Ingegneria - AA. 1996 - 1997.