Portale "Ingegneria e Campanologia" - Autore - Sommario - Mappa del Sito - Home
Meccanica del mezzo continuo e dei
materiali
AREA I - ARTE TECNICO-SCIENTIFICA (ATS)
Cap. ATS-H01 - Meccanica - Pag. ATS-H01.03
Gli argomenti trattati sono stati inseriti da Ing. Arch. Michele Cuzzoni nel 2012 - © Copyright 2007- 2025- e sono desunti dalla documentazione indicata in Bibliografia a fondo pagina
Gli elementi visti
![]() nella pagina precedente sono
esatti e di validità generale, a condizione che si considerino piccoli
spostamenti. Ma il dispositivo teorico è generico, quindi occorre esplicitare
l'equazione costitutiva per valutare il comportamento meccanico. Consideriamo
l'approssimazione del sistema che risponde in modo
elastico lineare: l'equazione costitutiva associata si scrive nel modo
seguente:
nella pagina precedente sono
esatti e di validità generale, a condizione che si considerino piccoli
spostamenti. Ma il dispositivo teorico è generico, quindi occorre esplicitare
l'equazione costitutiva per valutare il comportamento meccanico. Consideriamo
l'approssimazione del sistema che risponde in modo
elastico lineare: l'equazione costitutiva associata si scrive nel modo
seguente:
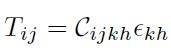 [H01-03-01]
[H01-03-01]
Dove:
Cijkh = costanti
![]() = tensore elastico di 34 = 81
componenti
= tensore elastico di 34 = 81
componenti
L'equazione
[H01-03-01] è di validità generale perché comprende ogni caso di simmetria
cristallina e/o anisotropia. Il numero delle componenti indipendenti di
![]() è
ridotto utilizzando relazioni matematiche:
è
ridotto utilizzando relazioni matematiche:
-
per la simmetria del tensore degli sforzi si ha:
![]() [H01-03-02]
[H01-03-02]
-
per la simmetria del tensore delle deformazioni si ha:
![]() [H01-03-03]
[H01-03-03]
-
considerazioni energetiche impongono che:
![]() [H01-03-04]
[H01-03-04]
Così si ottiene che
![]() ha 21 componenti indipendenti nel caso generale. Altre riduzioni di componenti
si hanno per la simmetria cristallina propria di ogni solido.
ha 21 componenti indipendenti nel caso generale. Altre riduzioni di componenti
si hanno per la simmetria cristallina propria di ogni solido.
La simmetria dei tensori
![]() e
e
![]() permette di utilizzare una notazione semplificata chiamata
notazione di Voigt: invece di rappresentare
permette di utilizzare una notazione semplificata chiamata
notazione di Voigt: invece di rappresentare
![]() con le corrispondenti matrici { Єij } e { Tij } è
più opportuno usare dei vettori colonna i cui elementi rappresentano le sei
componenti indipendenti dello sforzo.
con le corrispondenti matrici { Єij } e { Tij } è
più opportuno usare dei vettori colonna i cui elementi rappresentano le sei
componenti indipendenti dello sforzo.
Per consuetudine le direzioni cartesiane (x,y,z) si rappresentano sempre con gli indici (1,2,3); così le sei componenti indipendenti del tensore delle deformazioni si possono unificare in un solo vettore colonna così definito:
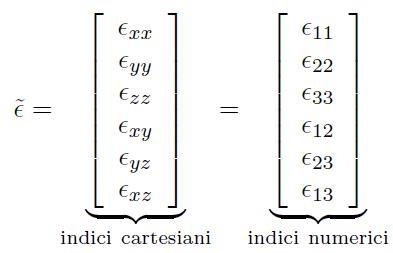 [H01-03-05]
[H01-03-05]
Quindi si identifica ogni coppia di indici con un unico indice numerico, come segue:
![]() [H01-03-06]
[H01-03-06]
Allora il vettore colonna
![]() viene indicato come:
viene indicato come:
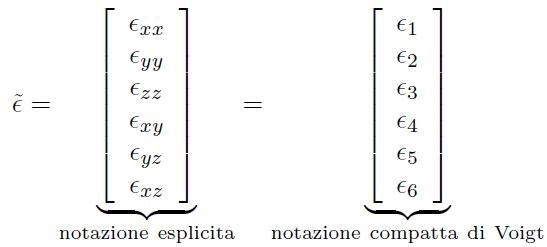 [H01-03-07]
[H01-03-07]
Allora il tensore degli sforzi diventa:
 [H01-03-08]
[H01-03-08]
In tal modo
![]() e
e
![]() sono i vettori associati ai tensori
sono i vettori associati ai tensori
![]() e
e
![]() ,
con la notazione di Voigt. Allora il tensore elastico Cijkh con 4
indici si trasforma in matrice quadrata di 6 righe e 6 colonne, chiamata
,
con la notazione di Voigt. Allora il tensore elastico Cijkh con 4
indici si trasforma in matrice quadrata di 6 righe e 6 colonne, chiamata
![]() .
Allora si ha:
.
Allora si ha:
![]() [H01-03-09]
[H01-03-09]
che diventa:
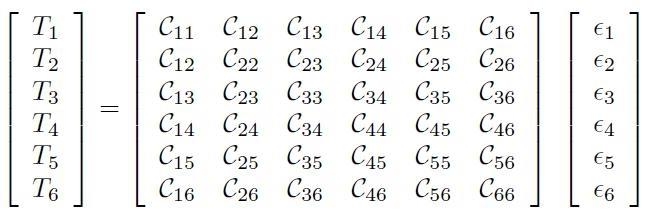 [H01-03-10]
[H01-03-10]
come si vede le componenti indipendenti del tensore elastico sono 21. La formula seguente dà le relazioni inverse:
![]() [H01-03-11]
[H01-03-11]
con
![]() ;
;
![]() [H01-03-12]
[H01-03-12]
con
![]() .
.
Le nuove quantità
![]() sono dette tensori di cedevolezza (o
flessibilità).
sono dette tensori di cedevolezza (o
flessibilità).
Si analizzi ora il mezzo continuo omogeneo e isotropo:
-
omogeneità: il comportamento meccanico del mezzo è identico in tutti i suoi punti: cioè il tensore elastico non dipende dalle coordinate del punto considerato;
-
isotropia: le proprietà meccaniche non dipendono dalla direzione considerata: tali proprietà sono invarianti per rotazioni.
Un esempio di mezzo elastico, omogeneo ed isotropo è quello di un materiale che, a parità di trazione, si allunga della stessa quantità indipendentemente dalla direzione lungo la quale viene applicato lo sforzo ed indipendentemente dal punto ove viene applicato lo stesso. Un mezzo che gode delle proprietà di omogeneità, isotropia e linearità (elasticità) è anche detto mezzo normale.
Per un mezzo normale esistono due sole componenti indipendenti del tensore
Poiché il tensore degli sforzi
Con questa sollecitazione il mezzo si allunga lungo la direzione x1 e si restringe nel piano (x2, x3), e si ha:
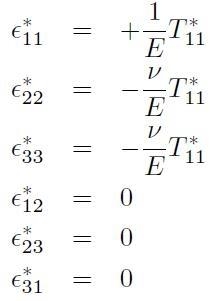
Il modulo di Young E descrive la variazione di lunghezza lungo la direzione di applicazione dello sforzo (prima formula in [H01-03-13]); il coefficiente di Poisson ν descrive invece l’entità della restrizione o dilatazione nelle direzioni ortogonali (seconda e terza formula in [H01-03-13]). Ovviamente nelle condizioni scelte non si osservano deformazioni di taglio.
Quando lo sforzo (pur sempre diagonale) assume carattere triassiale si può generalizzare le Eq. [H01-03-13] in modo immediato:
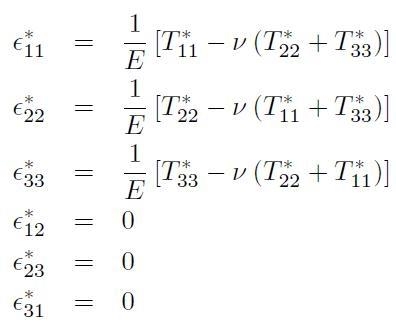 [H01-03-14]
[H01-03-14]
Il tensore di sforzo è diagonale e produce variazioni di lunghezza lungo i tre assi, senza variazioni angolari
La relazione costitutiva del mezzo è espressa in [H01-03-14], ma è valida solo sulla base ortonormale che diagonalizza il tensore degli sforzi. Se si generalizza in ogni sistema di riferimento occorre iniziare considerando che la [H01-03-14] si può scrivere in modo più compatto:
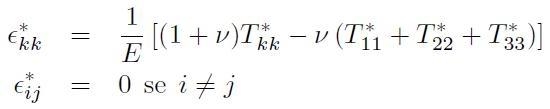 [H01-03-15]
[H01-03-15]
e vale la relazione matriciale:
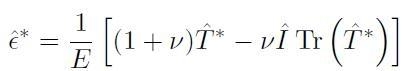 [H01-03-16]
[H01-03-16]
dove:
![]() = matrice identità 3 × 3
= matrice identità 3 × 3
![]() e
e
![]() sono diagonali.
sono diagonali.
Ruotando il sistema di riferimento con una matrice di
rotazione arbitraria
![]() ,
il tensore degli sforzi
,
il tensore degli sforzi
![]() diviene
diviene
![]() e il tensore delle deformazioni
e il tensore delle deformazioni
![]() .
La trasformazione si scrive:
.
La trasformazione si scrive:
 [H01-03-17]
[H01-03-17]
dove:
![]() = matrice trasposta di
= matrice trasposta di
![]() .
.
Utilizzando la [H01-03-16] tra i tensori diagonalizzati si ottiene:
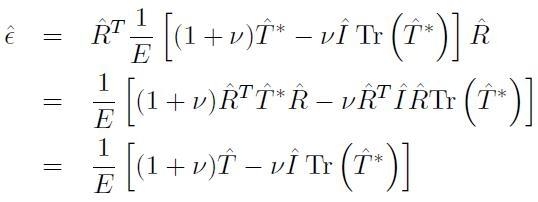 [H01-03-18]
[H01-03-18]
Utilizzando la proprietà commutativa
della traccia
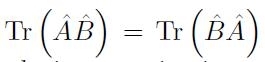 e l’ortogonalità
e l’ortogonalità
![]() , vale anche la relazione:
, vale anche la relazione:
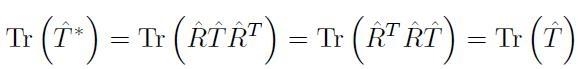 [H01-03-19]
[H01-03-19]
Combinando questi risultati, si ottiene la relazione costitutiva valida in qualsiasi sistema di riferimento (in cui sia il tensore di sforzo sia quello di deformazione non sono più in forma diagonale):
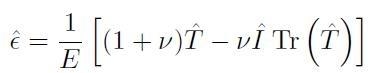 [H01-03-20]
[H01-03-20]
Esplicitando:
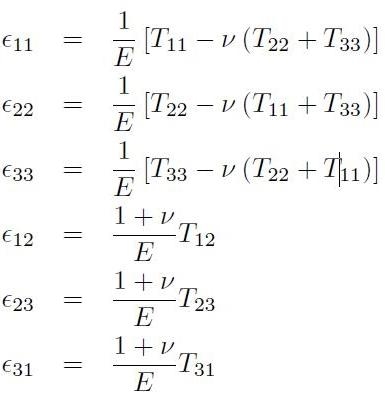 [H01-03-21]
[H01-03-21]
Si noti che in questo caso generico le variazioni angolari sono differenti da zero.
A partire dalla relazione fondamentale [H01-03-20] è possibile trovare la relazione inversa. Si calcoli la traccia del tensore delle deformazioni:
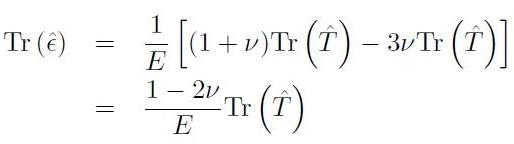 [H01-03-22]
[H01-03-22]
da cui si ottiene:
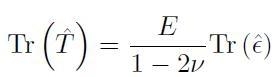 [H01-03-23]
[H01-03-23]
Dalla [H01-03-20] si ottiene il tensore degli sforzi:
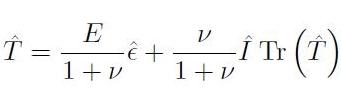 [H01-03-24]
[H01-03-24]
e, sostituendo il risultato di [H01-03-23], si ha:
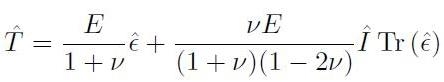 [H01-03-25]
[H01-03-25]
che rappresenta la relazione costitutiva nella forma inversa. A questo punto è possibile definire i coefficienti di Lamé indicati con i simboli μ e λ secondo queste relazioni:
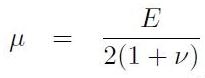 [H01-03-26]
[H01-03-26]
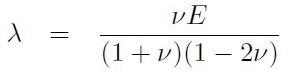 [H01-03-27]
[H01-03-27]
Si è perciò dimostrato che l’equazione costitutiva in regime lineare elastico per un mezzo omogeneo e isotropo è:
![]() [H01-03-28]
[H01-03-28]
La forma tensoriale di questa equazione può essere esplicitata in componenti:
![]() [H01-03-29]
[H01-03-29]
Si consideri il caso di uno sforzo idrostatico descritto dal tensore:
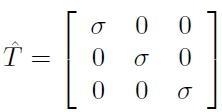 [H01-03-30]
[H01-03-30]
Con le equazioni costitutive, si può dimostrare che:
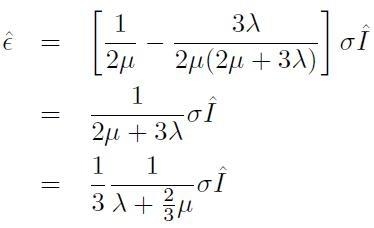 [H01-03-31]
[H01-03-31]
Si introduca il modulo di compressibilità K:
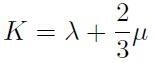 [H01-03-32]
[H01-03-32]
così che:
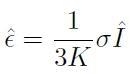 [H01-03-33]
[H01-03-33]
che riassume la relazione sforzo-deformazione nel caso di una pressione idrostatica di intensità σ. Si osservi inoltre che la relazione:
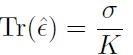 [H01-03-34]
[H01-03-34]
descrive la variazione volumetrica locale nel caso di sforzo idrostatico.
Si osservi, inoltre, che l’equazione costitutiva fondamentale può essere scritta in termini del modulo di scorrimento e del modulo di compressibilità:
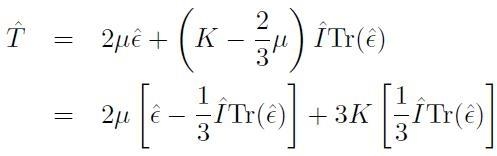 [H01-03-35]
[H01-03-35]
dove:
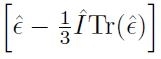 è la parte deviatorica
del tensore delle deformazioni;
è la parte deviatorica
del tensore delle deformazioni;
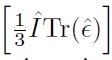 è la parte sferica
del tensore delle deformazioni.
è la parte sferica
del tensore delle deformazioni.
Questo risultato rappresenta l’applicazione in un caso particolare della proprietà generale tale per cui ogni tensore può sempre essere decomposto nelle sue parti sferica e deviatorica.
I cinque moduli di elasticità λ, μ,K,E, ν sono in relazione tra loro. Ognuno può essere scritto in funzione di altri due. Si ottiene in questo modo una serie di formule molto utili nelle applicazioni pratiche. Esse sono riportate in Tabella [H01-03-A] dove, leggendo la Tabella per righe, si trova ciascun modulo espresso in funzione di una coppia di altri moduli.

Tabella [H01-03-A]: Relazioni tra i moduli di elasticità.
I moduli E, λ, μ e K, che sono forze per unità di superficie, vengono misurati nel sistema internazionale in Pa (1 Pa=1 N/m2) o, più spesso, in MPa (1 MPa=1 N/mm2). Invece, il coefficiente di Poisson ν è una quantità adimensionale essendo definita come rapporto tra due deformazioni.
In Tabella [H01-03-B] si riportano i valori delle costanti E e ν per alcuni metalli. Come si può osservare, i valori di ν sono compresi tra 0.2 e 0.4 per la maggioranza dei metalli. Inoltre, in Tabella [H01-03-C] si riportano i valori delle altre costanti elastiche λ, μ e K per gli stessi elementi.
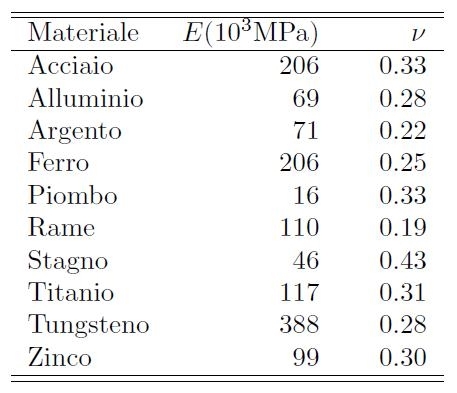
Tabella [H01-03-B]: Valori tipici delle costanti E e ν per alcuni metalli.
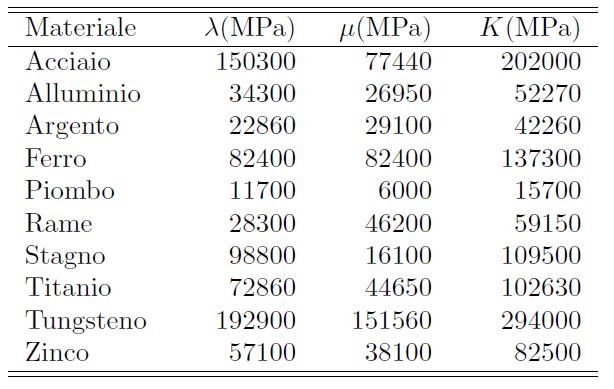
Tabella [H01-03-C]: Valori tipici delle costanti λ, μ e K per alcuni metalli.
Si presenta il calcolo esplicito del tensore degli sforzi, o di alcuni suoi elementi, in casi semplici.
Si consideri una sbarra costituita da un materiale omogeneo, isotropo, lineare con costanti di Lamé λ e μ. Essa viene deformato per semplice trazione lungo la direzione x1, in modo che la sua lunghezza vari dal valore l al valore l' = l + Δl.Calcolare il tensore degli sforzi associato a questa trazione.
L’unica componente non nulla del tensore delle deformazioni (notazione di Voigt) è Є1 = (Δl) / l in modo che:
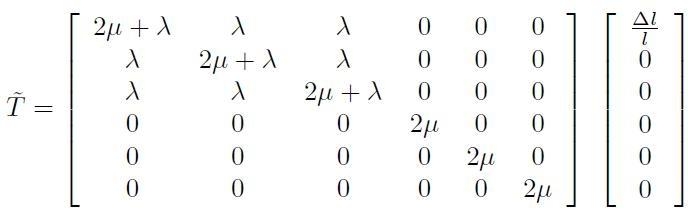 [H01-03-36]
[H01-03-36]
Da questa equazione si ricava il risultato che si sta cercando:
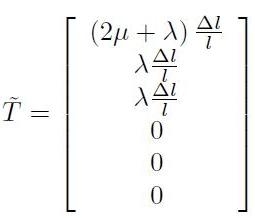 [H01-03-37]
[H01-03-37]
E' interessante notare che, sebbene la deformazione sia di trazione semplice, esistono tre diverse componenti non nulle del tensore degli sforzi:
-
la componente T1 rappresenta lo sforzo che occorre applicare per allungare la sbarra lungo la direzione x1;
-
le componenti T2 e T3 rappresentano gli sforzi tensili che è necessario applicare lungo le direzioni trasverse x2 e x3, rispettivamente, al fine di mantenere il valore della sezione della sbarra fisso al valore iniziale.
Lo stesso sistema di cui al caso precedente, è ora soggetto ad una deformazione di taglio puro. Il tensore delle deformazioni in notazione esplicita è dato da:
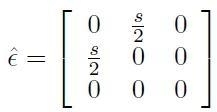
cui corrisponde in notazione di Voigt il vettore 6-dimensionale:
 [H01-03-38]
[H01-03-38]
Applicando ancora una volta l’equazione costitutiva lineare
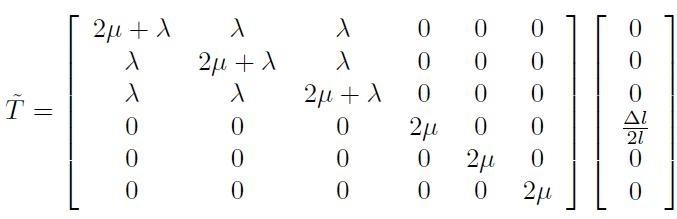 [H01-03-39]
[H01-03-39]
si ottiene immediatamente lo sforzo risultante:
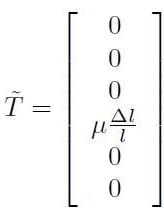 [H01-03-40]
[H01-03-40]
Questo risultato giustifica pienamente il nome “modulo di taglio” dato al coefficiente di elasticità μ: esso, infatti, mette in relazione l’entità della deformazione di taglio direttamente con lo sforzo di taglio applicato.
Portale "Ingegneria e
Campanologia" -
Autore -
Sommario
- Mappa del Sito -
Home
Bib-TS-147 - Michele Cuzzoni, Appunti di Scienza
delle Costruzioni - Università degli Studi di Pavia - Facoltà di Ingegneria -
AA. 1995 - 1996
Bib-TS-148 - Michele Cuzzoni, Appunti di Tecnica delle Costruzioni -
Università degli Studi di Pavia - Facoltà di Ingegneria - AA. 1996 - 1997.