Portale "Ingegneria e Campanologia" - Autore - Sommario - Mappa del Sito - Home
Strutturistica Chimica
AREA I - ARTE TECNICO-SCIENTIFICA (ATS)
Cap. ATS-F02 - Chimica - Pag. ATS-F02.20
Gli argomenti trattati sono stati inseriti da Ing. Arch. Michele Cuzzoni nel 2012 - © Copyright 2007- 2025- e sono desunti dalla documentazione indicata in Bibliografia a fondo pagina
-
Come determinare la Cella, il Sistema, il Reticolo ed il Gruppo Spaziale corretti?
I caso: cella monoclina con piano glide di tipo c nel piano xz
· Siano note le costanti di cella,
a, b, c, a, b, g.· Si siano misurati tutti i riflessi di indici hkl per
2q<2qmaxLe costanti di cella suggeriscono il sistema cristallino, non lo provano ! Ad esempio, 10.5, 9.7, 8.3, 90.0, 90.1, 90.0 è veramente monoclino o un errore di misura mi nasconde il fatto che sia ortorombico?
Dalla simmetria della diffrazione (intensità dei riflessi equivalenti, dopo correzioni per Lp e Abs],
· se hkl, h-kl, -h-k-l, -hk-l hanno intensità simili tra di loro (uguale entro l’errore sperimentale..]
e
· se -hkl, -h-kl, h-k-l, hk-l hanno intensità simili tra di loro (uguale entro l’errore sperimentale..]
ma appartengono a classi di intensità diverse, la simmetria di diffrazione è 2/m – simmetria Laue – il cristallo è monoclino con un angolo prossimo a 90°
Triclino -1
Monoclino 2/m
Ortorombico mmm
Tetragonale 4/m o 4/mmm
Trigonale o Romboedrico -3 o –3m
Esagonale 6/m o 6/mmm
Cubico m3 o m3m
· Si sia trovata la Cella 7.8 11.0 7.8 90.0 100.4 90.0 (Vol. 658)
· Si sia verificato che il Sistema è Monoclino (valgono gli equivalenti 2/m)
· Può questa cella essere descritta da una simmetria maggiore?
· Con la matrice [-1,0,-1; 0,1,0; 1,0,-1], trasformo la cella in:
· Ortorombico C di volume doppio [Vol. 1316]
· Cella 9.98; 11.0, 11.98, 90.0, 90.0, 90.0
· Trasformo gli hkl in h’k’l’
· Verifico se i riflessi ridenominati (h’k’l’) hanno simmetria mmm
Questo accade quando ci sono relazioni particolari fra assi ed angoli: nel nostro caso
a=c, a=g=90°:Come accorgersi di queste trasformazioni?
· Graficamente
· Algebricamente
· Con programmi adatti: Lepage; Tracer, Reduce-cell, Saint, etc.
Che vantaggi porta una descrizione a simmetria più alta?
Indubbiamente, che è necessario misurare meno riflessi
· Monoclino P: ¼ di tutti i possibili
· Ortorombico P: 1/8 di tutti i possibili
· Ortorombico C: 1/16 di tutti i possibili!
Data la maggiore simmetria, in cella ci saranno meno atomi indipendenti e la struttura sarà più facile da:
Risolvere, Modellare, Affinare, Descrivere. Di quanto sarà il guadagno?
1. La cella è 2 volte più grande
2. Gli elementi di simmetria sono 4 volte di più
3. In totale: Guadagno un fattore 2!
La presenza di elementi di simmetria traslazionale nei reticoli non primitivi viene effettuata osservando la assenza di intensità in particolari classi di riflessi nella lista completa di indici hkl.
Int = k(Lp](Abs]|Fo|2
Fo =
Sj fj exp(2pi(hx+ky+lz)) exp(-Bsin2q/l2)La somma si estende su tutti gli atomi in cella
Supponiamo di avere un Reticolo I
Per ogni atomo in x,y,z ce n’è uno in ½+x, ½+y, ½+z
Fo =
Sj/2 fj exp(2pi(hx+ky+lz)) exp(-Bsin2q/l2) +Sj/2 fj exp(2pi(h(½+x) +k(½+y) +l(½+z))) exp(-Bsin2q/l2), ovveroFo =
Sj/2 fj exp(2pi(hx+ky+lz)) exp(-Bsin2q/l2) [1+exp(pi(h+k+l))]Quando [1+exp(
pi(h+k+l)) = 0 ?·
Quando exp(pi(h+k+l)) = -1,·
ovvero quando (p(h+k+l)) = (2n+1)p·
ovvero quando (h+k+l) è in intero DISPARIConseguenza: in un reticolo I, i riflessi con h+k+l = dispari (2n+1) sono Assenti e hanno intensità NULLA
L’osservazione di intensità nulla per tutti i riflessi hkl di categoria (h+k+l) = dispari indica che il reticolo è I
Analogamente si deducono le seguenti condizioni:
Per i riflessi hkl sono assenti le classi allora:
nessuno P
h+k+l dispari I
h+k dispari C
h+l dispari B
k+l dispari A
h+k dispari
h+l dispari
k+l dispari F
-h+k+l non multiplo di 3 R
h-k+l non multiplo di 3 R
Appendice 6.1, p 224 Hammond: derivazione condizione F
Piano con scorrimento:
Prendiamo un Monoclino P (asse unico b) che abbia un piano glide c perpendicolare a b:
· per ogni atomo in x,y,z ce n’è uno in x, -y, ½+z
Fo =
Sj/2 fj exp(2pi(hx+ky+lz)) exp(-Bsin2q/l2) +Sj/2 fj exp(2pi(hx -ky +l(½+z))) exp(-Bsin2q/l2), ovveroper i riflessi con k=0 (classe h0l):
Fo =
Sj/2 fj exp(2pi(hx+lz)) exp(-Bsin2q/l2) [1+exp(pil)]Quando [1+exp(
pil)) = 0 ?·
Quando exp(pil) = -1,·
ovvero quando (pl) = -(2n+1)p·
ovvero quando l è in intero DISPARIConseguenza: in un gruppo spaziale con piano glide di tipo c (perpendicolare a b) i riflessi con l = dispari (2k+1) sono Assenti e hanno intensità NULLA
L’osservazione di intensità nulla per tutti i riflessi h0l di categoria l = dispari indica che è presente un glide
c ^ b.
Prendiamo un Monoclino P (asse unico b) che abbia un asse screw 21 parallelo a b:
·
per ogni atomo in x,y,z ce n’è uno in -x, ½+-y, -zFo =
Sj/2 fj exp(2pi(hx+ky+lz)) exp(-Bsin2q/l2) +Sj/2 fj exp(2pi(-hx +k(½+y) -lz)) exp(-Bsin2q/l2), ovvero per i riflessi con h=0 e l=0 (classe 0k0):Fo =
Sj/2 fj exp(2pi(ky)) exp(-Bsin2q/l2) [1+exp(pik)]Quando [1+exp(
pik)) = 0 ?·
Quando exp(pik) = -1,·
ovvero quando (pk) = -(2n+1)p·
ovvero quando k è in intero DISPARIConseguenza:
in un gruppo spaziale con asse screw di tipo 2
1 (parallelo a b)i riflessi con k = dispari (2k+1) sono Assenti e hanno intensità NULLA
L’osservazione di intensità nulla per tutti i riflessi 0k0 di categoria k = dispari indica che è presente un asse screw di tipo 21 parallelo a b.
Analogamente si può dedurre la seguente tabella:
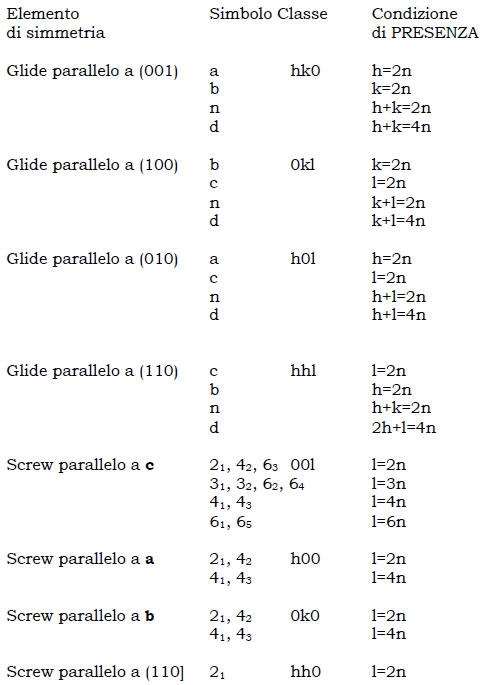
Dall’analisi delle condizioni di presenza (o assenza) delle diverse classi di riflessi si può dedurre la presenza di certi elementi di simmetria [ traslazionali! ]

Queste condizioni si chiamano assenze o estinzioni sistematiche.
1. Unendo le informazioni sulla Cella, sul tipo di Reticolo, sulla presenze di certi elementi di simmetria di tipo traslazionale, si può determinare(qualche volta in modo univoco!) il gruppo spaziale del cristallo (tra i 230 possibili)
2. Spesso il gruppo spaziale non può essere determinato univocamente:
· Altre misure (fisiche, chimiche, spettroscopiche) possono dare ulteriori informazioni
· Oppure bisogna tentare la soluzione in ciascuno dei gruppi spaziali ‘permessi’ e trovare il modello ‘migliore’ in uno di essi!

Sperimentalmente, può capitare che l’intensità diffratta da certi piani (hkl) sia nulla (ovvero uguale al rumore di fondo…)
Ciò può avvenire quando:
· Il valore di |F(hkl)|2 sia piccolo e non accessibile sperimentalmente
· Il valore di |F(hkl)|2 sia esattamente uguale a ZERO.
In quest’ultimo caso si parla di riflessi proibiti, estinti o sistematicamente assenti.
Evidenziare classi omogenee di riflessi proibiti dà informazioni essenziali per l’attribuzione del tipo di Reticolo di Bravais e degli elementi di simmetria con traslazione (screw e glide) nella cella, che individuano il GRUPPO SPAZIALE
Le condizioni di assenza sistematica si possono derivare:
· Considerando le conseguenza geometriche dettate da particolari centrature dei reticoli (ovvero derivandole dalla simmetria delle architetture dei cristalli).
· Considerando analiticamente l’espressione del fattore di struttura (che coinvolge il fenomeno della diffrazione.
Si prenda una cella una cella Cubica F di base a, b, c e la sua variante romboedrica P di base A, B, C.

H, K, L sono interi (pari o dispari); 2H, 2K e 2L sono interi pari
Quindi: (h+k), (h+l) e (k+l) sono interi pari
Un intero pari, se somma di due interi, è somma:
· Di due interi pari, o:
· Di due interi dispari, ma mai di un pari più un dispari!
Quindi: sono permessi (|F|¹0) solo quei riflessi con h,k,l o tutti pari o tutti dispari!
La struttura cristallina contenga atomi (di fattore si diffusione atomico f) posizionati sui punti reticolari di una cella fcc:
Le coordinate frazionarie (
un vn wn) saranno (000), (½½0), (½0½) e (0½½)Fhkl = f exp 2pi(h0+k0+l0) + f exp 2pi(h½+k½+l0) + f exp 2pi(h½+k0+l½) + f exp 2pi(h0+k½+l½)
Semplificando e ricordando che per una cella centrosimmetrica le componenti in seno spariscono..:
Fhkl = f [1 + cos
p(h+k) + cos p(h+l) + cos pi(k+l)]Dato che cos
pn = +1 per n pari e cos pn = -1 per n dispari,Fhkl dipende dalla parità degli indici h,k,l
Si dimostra facilmente che per: h,k,l tutti pari Fhkl = 4f
h,k,l tutti dispari Fhkl = 4f
h,k,l misti Fhkl = 0
Analogamente, per una cella cubica I (bcc) con atomi in (000) e (½½½):
Fhkl = f exp 2
pi(h0+k0+l0) + f exp 2pi(h½+k½+l½) = f [1 + cos p(h+k+l)]Quindi, quando (h+k+l) = intero pari, Fhkl = 2f
Quindi, quando (h+k+l) = intero dispari, Fhkl = 0
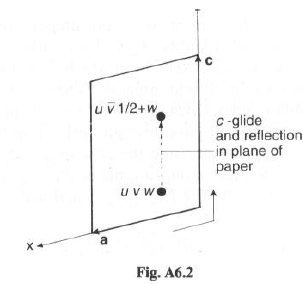
Da atomo in (uvw), il glide c ne genera uno simmetrico in (u –v ½+w)
Fhkl = f exp 2
pi(hu+kv+lw) + f exp 2pi[hu–kv+l(½+w)]Per la classe di riflessi con k=0, (h0l)
Fhkl = f exp 2
pi(hu+lw) + f exp 2pi[hu+lw] exp2pi l½] == f exp 2
pi(hu+lw) [1 + exp pi l]Dato che, per l intero dispari exp
pi l = -1, Fh0l = 0, ovvero:Nel piano di riflessi h0l, sono sistematicamente assenti quelli con l dispari!
La condizione di presenza è: in h0l, l = 2n
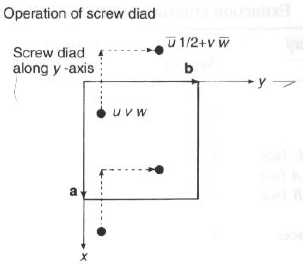
Da atomo in (uvw), l’asse 21 ne genera uno simmetrico in (-u ½+v -w)
Fhkl = f exp 2
pi(hu+kv+lw) + f exp 2pi[–hu+k(½+v)–lw]Per la classe di riflessi con h=0 e l=0, (0k0)
Fhkl = f exp 2
pi(kv) + f exp 2pi[½k+kv] = f exp 2pi(kv) [1 + exp pi k]Dato che, per k intero dispari exp
pi l = -1, F0k0 = 0, ovvero:Sul filare di riflessi 0k0, sono sistematicamente assenti quelli con k dispari!
La condizione di presenza è: in 0k0, k = 2n

Dato che dhkl
= a/ÖN e N = (h2 + k2 + l2),si possono mettere in sequenza ordinata N,
dhkl e hkl:
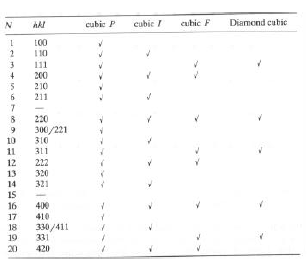
· Non ci sono quadrati di tre interi che sommano a 7, 15, etc.; ovvero, i cubici P (Pm-3m) hanno sequenza (fitta) con qualche gap.
· I cubici I (Im-3m) hanno una sequenza uniforme (meno fitta) senza gap.
· I cubici F (Fm-3m) hanno sequenza (meno fitta) 2 + 1 + 2 + 1 etc.
· I cubici tipo diamante (Fd-3m) hanno ulteriore estinzione: (h+k+l) dispari o pari 4n!
Quindi dall’analisi di:
· Geometria del reticolo reale (posizione dei picchi nel reciproco..)
· Simmetria dei riflessi del reticolo reciproco (confronto intensità)
· Estinzioni sistematiche per classi particolari di riflessi si possono individuare solo alcuni (pochi..) gruppi spaziali compatibili, tipicamente uno centrosimmetrico e alcuni dei suoi sottogruppi acentrici.
Esempio:
· Trovo che un cristallo dà intensità diffratta compatibile con un reticolo monoclino (e due angoli di 90°!);
· Attenzione, potrebbe essere un triclino con due angoli
casualmente vicini a 90° (all’interno dell’errore sperimentale): Verifico che la simmetria Laue sia rispettata, ovvero che:I(hkl) = I(-h-k-l)
¹ I(h-kl) = I(-hk-l) 2/m per un monoclino[Varrebbero I(hkl) = I(-h-k-l)
¹ I(h-kl) = I(-hk-l) per un triclino]· Cerco sul filare (0k0) eventuali estinzioni (per k = 2n+1)
· Cerco per tutti i riflessi eventuali estinzioni (==> reticolo di Bravais)
· Cerco nel piano (h0l) eventuali estinzioni (per h, o l, o (h+l) = 2n+1)
Tabelle di correlazione sulle Tabelle Internazionali
Portale "Ingegneria e
Campanologia" -
Autore -
Sommario
- Mappa del Sito -
Home
Bib-TS-081 - Prof. N. Masciocchi - Dispense del Corso di Laurea in Chimica - Insegnamento di strutturistica chimica
Bib-TS-082 - C.Hammond - The Basics of Crystallography and Diffraction - Ed. International Union of Crystallography and Oxford University Press, 240 pg. (Ed. italiana: Zanichelli)
Bib-TS-083 - J.P.Glusker & K.N.Trueblood - Crystal Structure Analysis: A Primer - Oxford University Press, 220 pg. (non tradotto).