Portale "Ingegneria e Campanologia" - Autore - Sommario - Mappa del Sito - Home
Strutturistica Chimica
AREA I - ARTE TECNICO-SCIENTIFICA (ATS)
Cap. ATS-F02 - Chimica - Pag. ATS-F02.15
Gli argomenti trattati sono stati inseriti da Ing. Arch. Michele Cuzzoni nel 2012 - © Copyright 2007- 2025- e sono desunti dalla documentazione indicata in Bibliografia a fondo pagina
· Costruzione geometrica astratta, basata sull’algebra vettoriale.
· Permette di interpretare quantitativamente osservazioni fisiche sperimentali, come gli ‘spettri’ di diffrazione di raggi X, elettroni, neutroni (da cui si ottengono le strutture cristalline e molecolari), o il comportamento degli elettroni nei solidi (spazio k).
Assiomaticamente, il reticolo reciproco può essere costruito a partire dai vettori di base a, b e c del reticolo diretto o reale.
Alternativamente, può essere introdotto collegando i concetti di zone (e assi) con piani (ed indici di Miller) in modo biunivoco:
· Dato che una famiglia di piani è univocamente caratterizzata dall’unica direzione della normale ai piani (Bravais, 1950, ‘assi polari’ (!)), ad ogni famiglia di piani (reale) viene associato un vettore (reciproco).
· Vettori (o punti) reciproci definiscono anch’essi un reticolo (reciproco), ogni punto del quale rappresenta una famiglia di piani.
· Il vantaggio di questa costruzione è che mette in luce la relazione tra famiglie di piani, la legge di Bragg e la geometria e direzione di raggi diffratti o riflessi da un solido cristallino.
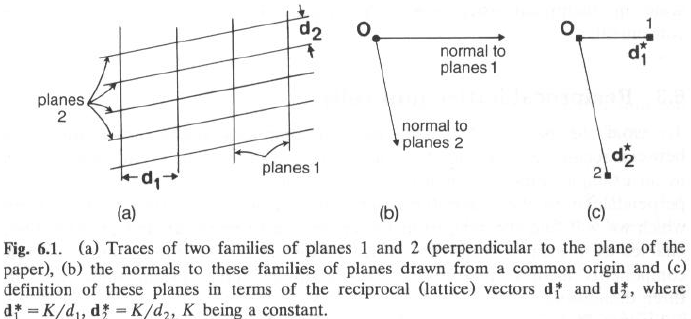
Una famiglia di piani qualsiasi è caratterizzata da: Orientazione nel cristallo (1) e Distanza tra i piani (2)
Come costruire un diagramma che traduca la figura in (a) in una diversa, ma più semplice, che contenga tutte le informazioni necessarie per ricostruire (a)? Ovvero, come costruire il reticolo reciproco dato il reticolo diretto o reale?
Regole di costruzione del reticolo reciproco:
· Si prende un’origine comune, da cui partono i vettori che caratterizzano le normali ai piani.
· Si troncano i vettori a valori d1* e d2*, lunghi K/d1 e K/d2
· K è una costante arbitraria, presa unitaria o, parlando di diffrazione di raggi X, K = l
· Questi vettori d1* e d2* sono vettori del reticolo reciproco, le cui lunghezze si misurano in [Lunghezza]-1, p.es. Ångstroms reciproci Å-1, o picometri reciproci, pm-1.
· P.es., se d1 = 0.5Å e K = 1, |d1*| = 1 / 0.5Å = 2.0 Å-1
· A vettori lunghi reali corrispondono vettori corti reciproci (e viceversa).
esemplificato per il sistema monoclino, con a e c nel piano
Si vuole determinare una base a*, b* e c* per lo spazio reciproco, in modo che ogni vettore reciproco sia esprimibile come combinazione lineare dei vettori di base reciproci.
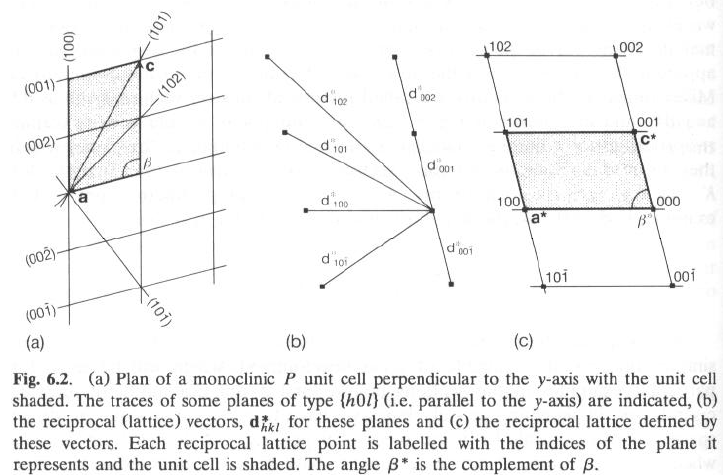
In (a) sono indicate:
· La cella reale di base (a, c), con angolo interassiale b
· Le tracce di diversi piani di tipo (h0l), cioè in zona con b, sono anche indicate tracce di piani ‘fittizi’ a cui sono assegnati indici di Laue (tipo 002, e 00-2)
· dhkl reali corti lunghi per indici di Miller alti: d002 < d001
In (b) e (c) sono mostrati:
· I vettori reciproci d* per ogni famiglia di piani, costruiti secondo le direzioni delle normali e con dhkl* = k/dhkl
· Vettori reciproci lunghi per indici di Miller alti: d*002 > d*001
· I punti finali dei vettori reciproci costituiscono anch’essi un reticolo (il reticolo reciproco) la cui cella unitaria reciproca è caratterizzata dai vettori a* = d*100 e |a*| = 1/d100; c* = d*001 e |c*| = 1/d001
· I vettori a* e c* non sono paralleli ad a e c, dato che le normali ai piani (100) e (001), nel reticolo monoclino non lo sono!
Estendendo nella terza dimensione, b* sta lungo la normale ai piani (010), ovvero esce dal foglio e coincide in orientazione (non in lunghezza) con b nel caso monoclino!
· Quindi in generale, l’orientazione di a e a* non è la stessa (né per b e c)
· Anche gli angoli interassiali cambiano (nel monoclino, b* = 180-b)
· Solo per sistemi retti (cubico, ortorombico e tetragonale) gli angoli si mantengono retti e le direzioni a/a* (e b/b*; c/c*) coincidono!
Qualsiasi vettore nello spazio reciproco sarà quindi combinazione lineare dei vettori di base a*, b* e c*, secondo: r* = d*hkl= ha* + kb* + lc*
Esempio: per la famiglia di piani (102) di fig. (a), d*102= 1a* + 0b* + 2c*
· La terna (hkl), che nello spazio diretto è associata ad una famiglia di piani paralleli, nello spazio reciproco indica le componenti del vettore d*hkl ad essi associato.
· Nello spazio diretto, ruvw = ua + vb + wc
I simboli [uvw] di una direzione sono le componenti di un vettore reale
· Nello spazio reciproco, d*hkl= ha* + kb* + lc*
Gli indici di Miller (hkl) sono le componenti di un vettore reciproco
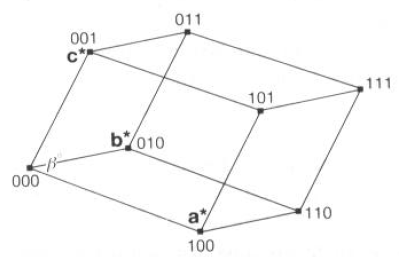
Cella unitaria RECIPROCA di un cristallo monoclino:
· E’ ancora monoclina, e possiede ai vertici terne intere.
· Ogni vertice rappresenta una famiglia di piani reali
· L’origine è contrassegnata dalle ‘coordinate reciproche’ 000, per cui d*000 = 0a* + 0b* + 0c* e d000 = 1/d*000 = ¥
· Piano reale con indici di Laue (¥¥¥)
· In cristalli con assi ortogonali, le direzioni a/a* (e b/b*; c/c*) coincidono: quindi: a.b = 0, a.b* = 0, etc.
· In cristalli cubici primitivi, la cella reciproca è anch’essa cubica P
· Ma per cristalli cubici con centrature I ed F cosa succede?
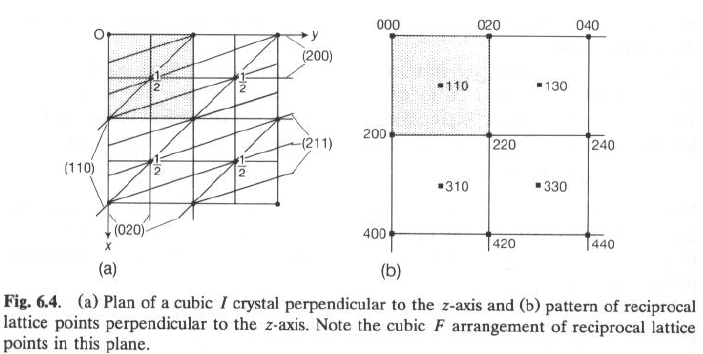
In (a): Cella cubica I reale (nel piano xy) con tracce di piani reali (hk0)
· La presenza di punti reticolari addizionali al centro della cella impone, come primo set di piani reticolari reali normali ad x, non (100), ma (200).
· Si deduce che il vettore reciproco in questa direzione sarà d*200 e non d*100
· Lo stesso vale per y e z; i vettori reciproci nelle tre direzioni saranno d*200, d*020 e d*002
· Tuttavia, nella direzione [110] si incontra la famiglia di piani reticolari reali (110), che genera un punto reticolare reciproco al centro della faccia a*b* della cella reciproca.
· Continuando in modo sistematico, si può costruire il reticolo reciproco corrispondente al reticolo reale Cubico I: Tale reticolo è un Cubico F !
· Analogamente, il reticolo reale Cubico F si trasforma nel reticolo reciproco Cubico I !
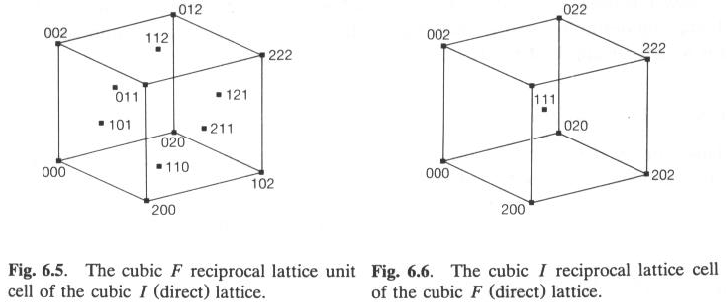

· Relazioni fra vettori di base a, b, c e a*, b* e c*
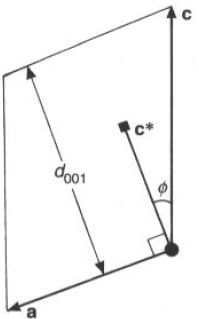
Cella monoclina con a e c nel piani, b normale.
Per costruzione, c* è normale sia ad a che a b.
Ovvero: c*.a = 0 e c*.a = 0
Analogamente, per a* e b* valgono le:
a*.c = 0 e a*.b = 0
b*.a = 0 e b*.c = 0
Invece, per c.c* = |c||c*| cos f ?
Dato che |c*| = 1/d001 ; |c| cos f = d001
c.c* = |c||c*| cos f = d001/d001 = 1 e anche a.a* = b.b* =1
Quindi, si può definire spazio reciproco dello spazio reale (la cui base è costituita da a, b, c) quello generato dai vettori a*, b* e c*, tali per cui:
a.a* = 1 a.b* = 0 a.c* = 0
b.a* = 0 b.b* = 1 b.c* = 0
c.a* = 0 c.b* = 0 c.c* = 1
Definizione Assiomatica
· Il volume di una cella reale è dato da V = a.(bxc)
· Dato che (bxc) è un vettore parallelo ad a* e di modulo uguale all’area della faccia della cella definita da b e c, a* = (bxc)/V = (bxc)/a.(bxc)
· Lo stesso vale per b* e c*
· Se definisco V* = a*.(b*xc*), posso completare le relazioni che definiscono i vettori reciproci.
· a* = (bxc)/V b* = (cxa)/V c* = (axb)/V
· a = (b*xc*)/V* b = (c*xa*)/V* c = (a*xb*)/V*
· La regola di addizione
Siano dati due piani (h1k1l1) e (h2k2l2) che giacciono in una zona. L’indice di Miller di qualsiasi altro piano (HKL) in zona con questi piani è dato da:
H = (mh1 + nh2); K = (mk1 + nk2); L = (ml1 + nl2),
con m ed n interi (piccoli);
Ovvero: (HKL) è combinazione lineare di (h1k1l1) e (h2k2l2)
basta fare la somma vettoriale di due vettori reciproci d*
d*(mh1+nh2)(mk1+nk2)(nl1+ml2) = d*m(h1k1l1) + d*n(h2k2l2)
Esempio: d*102 = d*101 + d*001
· La legge di ZONA (o legge di Weiss)
Se un piano (hkl) giace in una zona [uvw] (ovvero, se la direzione [uvw] è parallela al piano (hkl)) allora:
hu + kv + lw = 0
Un piano reale diventa un vettore reciproco d*hkl
La direzione reale è caratterizzata da ruvw
Se un piano reale (hkl) giace in una zona [uvw], allora d*hkl e ruvw sono perpendicolari
Il prodotto scalare d*hkl . ruvw= (ha* + kb* + lc*).(ua + vc + wc)= 0
Tenendo conto dei prodotti scalari (reale . reciproco) = 0 o 1, si trova:
d*hkl . ruvw= hu + kv + lw = 0
Generalizzazione della legge di Weiss:
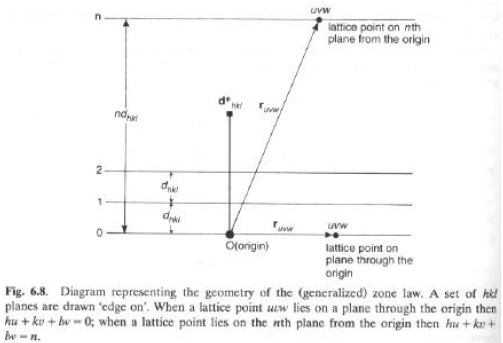
Si prenda un punto reale uvw (vettore ruvw) che giace sul piano reale (hkl).
Il piano passa per l’origine O
Per costruzione, d*hkl e ruvw sono perpendicolari
d*hkl . ruvw = hu + kv + lw = 0
Il piano non passa per l’origine, ma ne è distante ndhkl (n-esimo piano della famiglia)
La condizione per cui un punto ruvw sia in questo piano è che le componenti di ruvw perpendicolari al piano siano uguali a ndhkl ovvero:
ruvw . i = ndhkl
dove i è un versore (vettore unitario) perpendicolare ai piani
Per definizione, i = d*hkl /|d*hkl| = d*hkl dhkl
ruvw . i = ruvw
. d*hkl dhkl = ndhkl , da cui ruvw
. d*hkl = n
Ovvero: d*hkl . ruvw = hu + kv + lw = n
· Valori di spaziature d tra piani reali (hkl)
d*hkl .d*hkl =|d*hkl|2 = 1/d2hkl = (ha*+kb*+lc*).(ha*+kb*+lc*)
Dato che solo per sistemi retti a*.b* = a*.c* = etc. = 0
E ricordando che: a*.a* = 1/a2
1/d2hkl = ha*.ha* + kb*.kb* + lc*.lc* = h2/a2 + k2/b2 + l2/c2
· Angolo r tra le normali ai piani (h1k1l1) e (h2k2l2)
Dato che a . b = |a| |b| cos r , cos r = d*h1k1l1 . d*h2k2l2 /. |d*h1k1l1| | d*h2k2l2 |,
che dà una espressione semplificata solo per cristalli cubici.
· Asse di zona all’intersezione di due piani (h1k1l1) e (h2k2l2)
E’ definito da ruvw = d*h1k1l1 x d*h2k2l2 con un po’ di algebra:
ua + vb + wc = a(k1l2-k2l1) + b(l1h2-l2h1) + c(h1k2-h2k1)
da cui: u = (k1l2-k2l1) ; v = (l1h2-l2h1) ; w = (h1k2-h2k1)
· Piano contenente due direzioni [u1v1w1] e [u2v2w2]
Dato che un piano è definito da d*hkl , il prodotto ru1v1w1 x ru2v2w2 dà:
h = (v1w2-v2w1) ; k = (w1u2-w2u1) ; l = (u1v2-u2v1)
Portale "Ingegneria e
Campanologia" -
Autore -
Sommario
- Mappa del Sito -
Home
Bib-TS-081 - Prof. N. Masciocchi - Dispense del Corso di Laurea in Chimica - Insegnamento di strutturistica chimica
Bib-TS-082 - C.Hammond - The Basics of Crystallography and Diffraction - Ed. International Union of Crystallography and Oxford University Press, 240 pg. (Ed. italiana: Zanichelli)
Bib-TS-083 - J.P.Glusker & K.N.Trueblood - Crystal Structure Analysis: A Primer - Oxford University Press, 220 pg. (non tradotto).