Portale "Ingegneria e Campanologia" - Autore - Sommario - Mappa del Sito - Home
Strutturistica Chimica
AREA I - ARTE TECNICO-SCIENTIFICA (ATS)
Cap. ATS-F02 - Chimica - Pag. ATS-F02.13
Gli argomenti trattati sono stati inseriti da Ing. Arch. Michele Cuzzoni nel 2012 - © Copyright 2007- 2025- e sono desunti dalla documentazione indicata in Bibliografia a fondo pagina
Come individuare generiche direzioni, piani, assi (anche in sistemi non ortogonali)?
E se avessimo scelto il punto Q, piuttosto che P (che era arbitrario…)?
· Assi di cella (con angoli interassiali)
· Reticolo di Bravais
· Simmetria puntuale (classi)
· Simmetria spaziale
Attribuiremo ‘coordinate’ (terne di numeri, per lo più interi) ad enti geometrici i più disparati:
Es: Diagonale di corpo di un cubo <111>
Forma del cubo {100}
Forma di un ottaedro {111}
Passaggi logici fondamentali:
· Definire esattamente la cella ed il reticolo di Bravais.
· Utilizzare coerentemente celle e descrittori diversi, eventualmente conoscendo come passare da cella a cella e tra relativi descrittori
· P.es. Trigonale – Esagonale
· P.es. Romboedrico con a speciale: ==> Cubico F o Cubico I
ZONA: Collezione di facce o piani in un cristallo le cui intersezioni sono parallele.
ASSE DI ZONA: La direzione comune alle intersezioni di piani di una ZONA Qualsiasi direzione in un cristallo può essere un ASSE DI ZONA, quindi i concetti di ASSE DI ZONA e DIREZIONE sono sinonimi.
Esempio: Matita (prisma esagonale):
Le facce laterali hanno intersezioni tutte parallele tra di loro, costituiscono una ZONA, con ASSE lungo la direzione di allungamento della matita.
N.B. Il numero di facce che appartengono ad una ZONA non è limitato:
Un prisma retto a sezione dodecagonale ha 12 facce in ZONA Oppure:
Per un prisma retto di tipo ortorombico, facce diverse (di diversa estensione, simmetria e natura) sono in ZONA tra loro, a seconda che si scelga la DIREZIONE x, y o z.
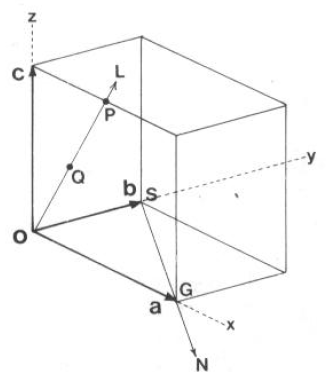
· Si voglia caratterizzare la direzione OL.
· Si prende una retta passante per l’origine della cella unitaria.
· Si individua un punto P sulla direzione OL, tale che |OP| non sia nullo.
· Si individuano le coordinate frazionarie (degli assi di cella a, b e c) del punto P. In questo caso P è in ½, 0, 1.
· Si rinormalizzano queste coordinate ad interi tali che i rapporti vengano mantenuti e le si inserisce tra parentesi QUADRE: [1 0 2]
· [102] è il SIMBOLO per la DIREZIONE OL
· Q ha coordinate ¼,0,½; normalizzando, si ha ancora [102]
Esempio: Calcolare il simbolo della direzione SN
· Mettendo l’origine in S, N ha coordinate 1,-1,0, cioè [1-10]
· (One, Bar One, Zero: Bar One è Uno SOPRASEGNATO)
Le DIREZIONI nei cristalli sono vettori, i cui componenti in termini dei vettori di base (della cella unitaria) sono, p.es.:
per OL: r102 = 1a + 0b + 2c
per SN: r1-10 = 1a - 1b + 0c
Una DIREZIONE generale si indica con [uvw] e corrisponde a: r
uvw = ua + vb + wcCon questa notazione, i vettori di base (a, b e c) si indicano spesso con:
a (asse x) = [100] b (asse y) = [010] c (asse z) = [001]
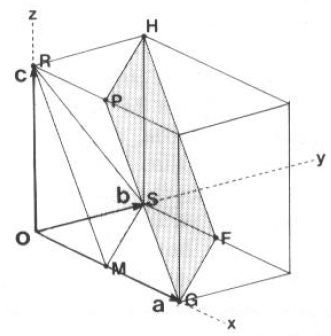
Il piano NON deve passare per l’origine.
· Che simbolo assegniamo al piano RMS (che si estende in modo infinito nel cristallo...)? Il triangolo RMS è solamente la porzione contenuta nella cella unitaria della figura.
· Stiamo assegnando un simbolo non ad un PIANO, ma ad una FAMIGLIA di PIANI PARALLELI, come RMS e HFPG (e quello che passa per l’origine!).
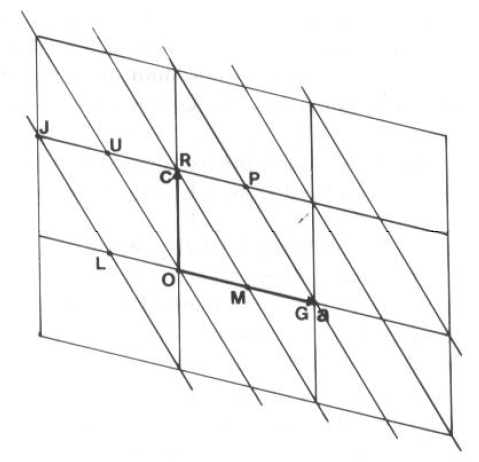
Piani paralleli diversi intersecano origini di celle diverse, ma hanno identiche inclinazioni e corrispondono a traslazioni reticolari.
· Per RMS, individuare le intercette sugli assi (½a, b, c)
· In termini frazionari = ½, 1, 1
· Individuare i RECIPROCI: 2, 1, 1; inserirli in parentesi TONDE (211)
· (211) è l’indice di Miller del piano RMS
E per il piano HFPG?
· Estendendo il piano oltre i limiti di cella: (1a, 2b, 2c)
· In termini frazionari = 1, 2, 2
· Reciproci: 1, ½, ½, che, normalizzati ad interi, danno (211)
E per il piano all’origine?
· Intersezioni in 0, 0, 0: Indice di Miller indeterminato (¥¥¥)
E per un piano dall’altra parte dell’origine (JL)?
Intersezioni in -½a,-1b,-1c Indice di Miller (-2-1-1), cioè (211)
Gli indici di Miller (hkl) di un generico piano si derivano dalle posizioni delle intercette frazionarie sui diversi assi del primo piano della famiglia:
Intercette in: a/h, b/k, c/l
La famiglia di piani (hkl) contiene il primo piano con intercette a/h, b/k, c/l
Un secondo piano parallelo ha intercette 2a/h, 2b/k, 2c/l
Ovvero: Si incontrano h piani nel passare da un vertice della cella al vertice successivo lungo a.
Analogamente si incontrano k piani lungo b e l piani lungo c.
Gli indici di Miller si applicano anche a FACCE di poliedri (o cristalli macroscopici)
· Convenzionalmente, l’origine è al centro del cristallo.
· L’intercetta sarà a diversi milioni di passi di cella (in funzione delle dimensioni del cristallo).
· I rapporti delle intercette frazionarie saranno comunque esprimibili da numeri INTERI: Indici di Miller di una faccia saranno quelli della famiglia cui la faccia appartiene!
· Collegamento con la legge degli indici razionali (Haüy!)
· Quando un piano è in ZONA con una direzione, la sua intercetta con essa è infinita.
· Per la faccia frontale di un prisma retto (z verticale), l’intercetta è in n,¥,¥, i cui reciproci sono 1/n, 0, 0: indici di Miller (100)
Generalmente, gli indici di Miller sono interi primi tra loro. In qualche caso usare dei multipli comuni permette di individuare specificatamente un piano all’interno di una famiglia (per reticoli non primitivi…)
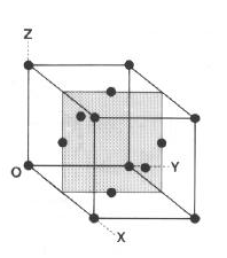
· Cubico F: Il piano indicato ha intercette ½, ¥, ¥ ed indici di Miller (200).
· La famiglia di piani con indici (100) deriva dalla normalizzazione di intercette del tipo (n00).
· (100) e (200) indicano due piani specifici, paralleli tra loro, che descrivono piani fisici differenti.
· Facce esterne di cristalli non soffrono di questa ambiguità.
Uso dei simboli di asse di zona e di indici di Miller per descrivere simbolicamente la simmetria dei cristalli.
Esempio per sistema cubico:
assi coordinati: x = [100]; y = [010]; z = [001]
(assi nel verso negativo) -x = [-100]; -y = [0-10]; -z = [00-1]
Ma gli assi sono intercambiabili ed equivalenti per simmetria:
[100]; [010]; [001]; [-100]; [0-10]; [00-1] = <100>
In parentesi TRIANGOLARI si individuano tutte le varianti per simmetria (scambi e permutazioni incluse).
Collettivamente,
· Le 4 diagonali di corpo del cubo si esprimono con <111>, di cui esistono 8 varianti:
[111]; [-111]; [1-11]; [11-1]; [-1-11]; [-11-1]; [1-1-1]; [-1-1-1]
· I 12 assi binari (spigolo a spigolo) sono inclusi in <110>
· Per una direzione generica <uvw> ci sono 48 varianti
Si possono raggruppare in FORME {parentesi graffe} indici di Miller di piani equivalenti per simmetria:
{100} è la collezione di 6 facce o piani: Forma del CUBO
{111} è la collezione di 8 facce o piani: Forma dell’OTTAEDRO
Se da {111} tolgo il centro di simmetria, rimangono quattro facce: (111); (1-1-1); (-11-1); (-1-11): forma del TETRAEDRO SOLAMENTE in cristalli cubici vale la regola che direzioni [uvw] sono perpendicolari a piani (uvw).
· In generale questo NON è vero:
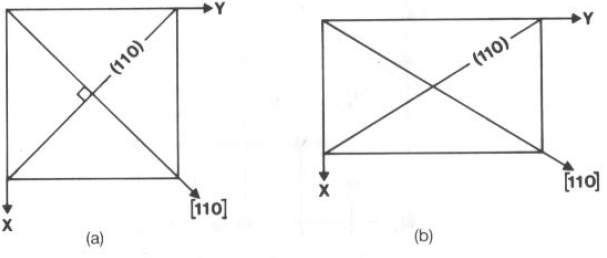
(anche esistono casi speciali: (100) e [100] in sistemi RETTI).
Portale "Ingegneria e
Campanologia" -
Autore -
Sommario
- Mappa del Sito -
Home
Bib-TS-081 - Prof. N. Masciocchi - Dispense del Corso di Laurea in Chimica - Insegnamento di strutturistica chimica
Bib-TS-082 - C.Hammond - The Basics of Crystallography and Diffraction - Ed. International Union of Crystallography and Oxford University Press, 240 pg. (Ed. italiana: Zanichelli)
Bib-TS-083 - J.P.Glusker & K.N.Trueblood - Crystal Structure Analysis: A Primer - Oxford University Press, 220 pg. (non tradotto).