Collezione di elementi caratterizzati da una operazione, detta di moltiplicazione tale che:

1. Esiste l’elemento neutro;

2. Per ogni elemento esiste l’elemento inverso;

3. Il prodotto tra due elementi appartiene alla collezione.

Esempi:

L’insieme dei numeri interi, negativi, nulli e positivi. Esso costituisce gruppo rispetto all’operazione di addizione (+), con elemento nullo lo 0 ed inverso inv(n) = (-n), dato che per ogni n:

1. n = n + 0

2. 0 = n + (-n)

3. n+m appartiene all’insieme

L’insieme dei numeri razionali (tranne lo zero!). Esso costituisce gruppo rispetto all’operazione di moltiplicazione (*), con elemento nullo 1 ed inverso inv(n) = n-1, dato che per ogni n:

1. n = n * 1

2. 1 = n * inv(-n)

3. n*m appartiene all’insieme

Gruppo di simmetria: collezione di operazioni (non elementi!) di simmetria che soddisfano le definizioni di gruppo, e per cui il prodotto è l’applicazione successiva ordinata delle operazioni di base.

Non è detto che A*B = B*A, ovvero il prodotto non è necessariamente commutativo (vedi l’algebra delle matrici…).

Per i gruppi di simmetria, E (o 1) è l’elemento neutro.

inv(-1) = E; inv(m) = E;

inv(X) = rotazione di –360/X°;

inv(-X) = rotoinversione di –360/X°

INDICE

Ogni molecola (rigida e statica…) ha una ben determinata simmetria, caratterizzata da elementi di simmetria ed operazioni di simmetria che costituiscono un gruppo.

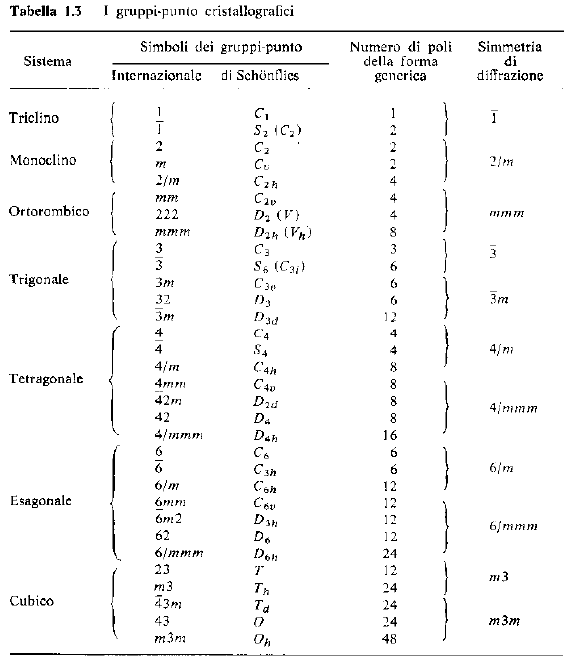
Il gruppo puntuale contiene tutte le operazioni di simmetria e può essere caratterizzato dalla notazione di Schönflies (tipica per i chimici) o quella di Hermann-Mauguin (tipica per i fisici, i cristallografi ed i mineralogisti).

Esiste una corrispondenza biunivoca tra le due notazioni.

E’ anche possibile caratterizzare la morfologia di un cristallo (o qualsiasi altro oggetto finito) con le stesse notazioni.

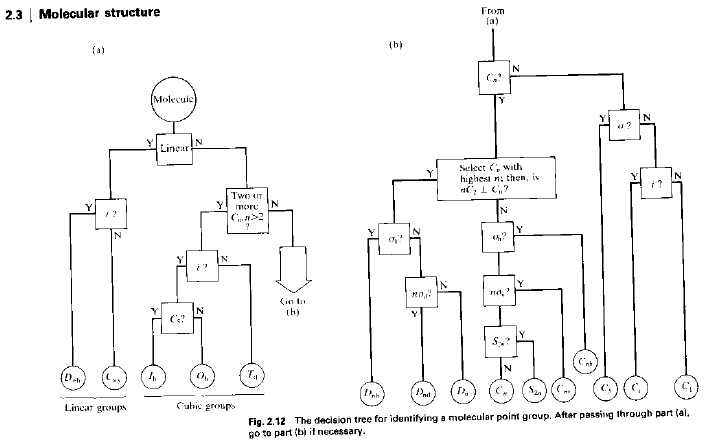
il primo simbolo si riferisce alla direzione x (o y, o z) il secondo agli assi ternari, il terzo agli assi paralleli alle diagonali di faccia (od ai piani normali ad esse)

Quindi, per un cubo: 4/m 3 2/m, spesso abbreviato in m3m

Per un tetraedro, il gruppo puntuale ha simbolo -43m

i tre simboli riguardano gli assi x, y e z, nell’ordine

Un prisma retto ha simmetria 2/m 2/m 2/m (ovvero mmm)

Una piramide rettangolare retta ha simmetria mm2

l’unico simbolo si riferisce all’asse y: può essere 2, m o 2/m

Esistono solo 1 e –1

il primo simbolo si riferisce all’asse unico (z) gli altri due a direzioni perpendicolari ad esso, lungo gli assi x (o y) e le bisettrici di ciascun quadrante (o sestante)

Il gruppo puntuale è –4 2 m

Quanto sono comuni queste classi cristalline?

· Non esistono casi reali di cristalli delle classi 432 e –6

· 50% dei composti inorganici = m e 2/m

· 30-40% dei composti organici = classe 2/m

· composti biologici chirali = spesso classe 2

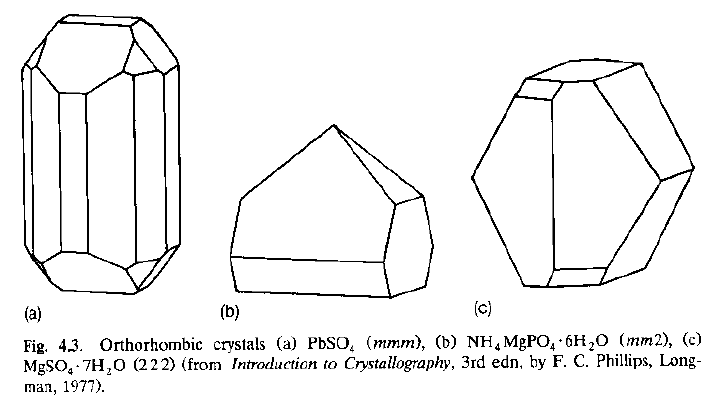
· Questi tre cristalli hanno ovviamente forme diverse (ed anche simmetrie) diverse: appartengono a classi cristalline differenti (gruppi puntuali diversi).

· Una volta aggiunto il centro di inversione (che tutti i reticoli posseggono!), questi cristalli hanno simmetria puntuale mmm, e quindi appartengono tutti al sistema ortorombico.

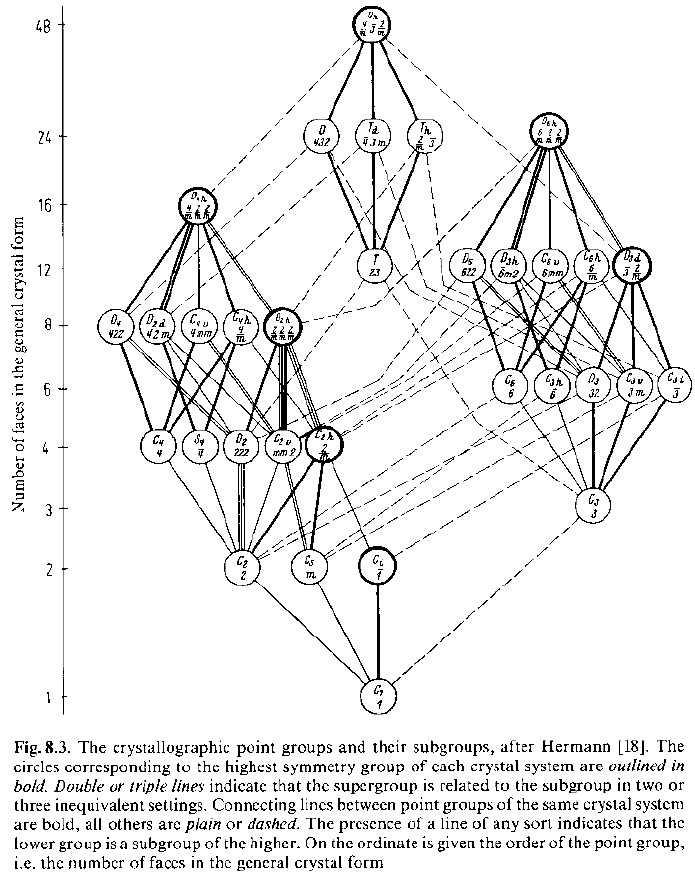
· Così come erano stati individuati 10 gruppi planari cristallografici indipendenti, esistono solo 32 gruppi puntuali 3D cristallografici, compatibili cioè con la traslazione. (J.F.C.Hessel, 1830)

Le proprietà fisiche (ottiche, termiche, magnetiche, etc.) sono normalmente espresse in termini di coefficienti, ovvero come rapporto tra due quantità misurabili.

Esempi: A = ecl (coefficiente di estinzione molare) m = aE (polarizzabilità)

Le quantità misurabili sono spesso vettori (dotati di modulo e direzione), o più raramente scalari (non dipendono dalla direzione)

I cristalli sono oggetti anisotropi e comportano una descrizione delle proprietà fisiche in termini vettoriali.

Solo in qualche caso (alte simmetrie, cristalli isotropi) o per certe proprietà (T, calore, e, etc.) si incontrano grandezze scalari.

Enantiomorfismo (cristalli non sovrapponibili alla propria immagine speculare).

· Il gruppo puntuale (1) – C1 è detto asimmetrico;

· Gli altri gruppi puntuali che hanno solamente assi di rotazione propri sono detti chirali o dissimmetrici;

I gruppi enantiomorfici sono:

X: (1), 2, 3, 4, 6 gruppi Cn;

X2: 222, 32, 422, 622 gruppi Dn;

X3: 23, 432 gruppi T, O

· Molecole enantiomorfiche sono dette enantiomeri.

· Cristalli che contengono un enantiomero risolto possono solamente appartenere a una delle classi enantiomorfe. Attività ottica: abilità di molecole o cristalli a ruotare il piano della luce polarizzata.

· Può esistere solamente in gruppi puntuali enantiomorfici.

· Il cristallo è otticamente attivo, ma la sua attività ottica è persa quando esso è sciolto o fuso.

· Sono enatiomorfiche sia la morfologia che la struttura.

· Esempi: MgSO4.7H2O (222), SiO2 (quarzo, 32), NaClO3 (23).

· I cristalli di molecole enantiomere sono enantiomorfi, e l’attività ottica viene conservata per dissoluzione o fusione.

La proprietà ottica è assegnata non all’impaccamento cristallino, ma alla dissimmetria molecolare.

Esempi: acido D-tartarico (2), otticamente attivo

acido DL-tartarico (-1), racemato, inattivo

acido meso-tartatico (-1), inattivo

· Cristalli dei gruppi puntuali m, mm2, -4 e –42m possono mostrare altre proprietà ottiche, diverse dalla rotazione lella luce polarizzata (birifrangenza, pleocroismo, dispersione)

Capacità di un cristallo di sviluppare separazione di cariche su facce opposte per pressione o tensione lungo certe direzioni.

· Esempio: cristalli di quarzo (32) tagliati normalmente ad a.

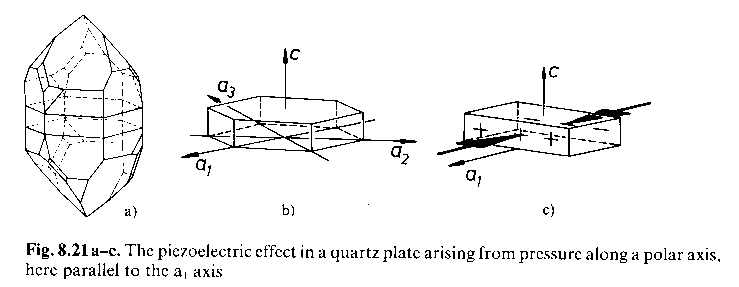
· La direzione di pressione o tensione è una direzione polare.

· Assi polari sono quelli la cui inversione porta a cambiamento di proprietà fisiche (direzioni parallele ed antiparallele).

· Pressione o tensione sviluppano cariche opposte.

· Effetto reversibile: applicando un campo elettrico, i cristalli si espandono o si comprimono.

· L’effetto piezoelettrico si osserva solamente in gruppi puntuali che hanno assi polari (che, ovviamente, sono noncentrosimmetrici).

· I gruppi in cui l’effetto piezoelettrico è possibile sono 20 dei 21 gruppi che non posseggono centri di inversione (tranne il 432!).

· Applicazioni tecnologiche: amplificatori, microfoni, componenti elettronici.

· Radio a Galena (PbS, -43m), bilance e orologi al quarzo.

Capacità di un cristallo a sviluppare cariche opposte su facce opposte se scaldato. Se raffreddato, si sviluppano cariche di segno opposto.

Esempio: Tormalina (3m).

· I cristalli piroelettrici hanno un dipolo permanente. Il cambio di temperatura modifica l’entità (modulo) del dipolo.

· L’effetto è temporaneo, per conduzione le cariche vengono più o meno rapidamente dissipate.

· L’effetto piroelettrico è possibile solamente in quei gruppi puntuali le cui operazioni di simmetria non alterano la direzione del dipolo, ovvero i gruppi 2, 3, 4 e 6; mm2, 3m, 4mm e 6mm (il dipolo giace lungo l’asse unico) e i gruppi 1 ed m. (10 gruppi puntuali).

· L’effetto piroelettrico si osserva solamente in questi 10 gruppi puntuali (che, ovviamente, sono noncentrosimmetrici).

· I 10 gruppi polari sono quindi: 1 2 3 4 6 - m mm2 3m 4mm 6mm

· Tutti i gruppi ‘piroelettrici’ sono anche piezolettrici (NON vale il contrario!)

Per molecole ‘isolate’, posseggono un momento dipolare (permanente) non-nullo quelle appartenenti alle classi di simmetria che premettono la piroelettricità.

La misura del momento dipolare permette di ottenere informazioni stereochimiche di molecole normalmente gassose, non facilmente ottenibili come cristalli.

Esempio: PF3 ha un momento dipolare, BF3 no.

Infatti, PF3 è piramidale (-6m2), mentre BF3 è planare (3m).

capacità di un cristallo a sviluppare cariche opposte su facce opposte se sottoposto ad un campo elettrico.

Valgono le stesse regole della piroelettricità.

Esempio: BaTiO3.

· Ad alta T (> T Curie), cubico m3m (struttura perovskite);

· A bassa T (<T Curie), si distorce (due assi si accorciano, uno si allunga): tetragonale 4mm;

· Ulteriore diminuzione di T porta successivamente a mm2 e poi a 3m (tutti gruppi polari).

INDICE