Il sistema cristallino di un campione può essere determinato dall’osservazione morfologica o da una serie di misure di proprietà fisiche.

· P.es. cristalli che mostrano simmetria cubica (NaCl) ovviamente appartengono al sistema cubico. La forma della cella cristallina e quella del cristallo coincidono.

· Tuttavia, altre forme cristalline sono compatibili con la simmetria puntuale del reticolo cubico; in questi casi la forma della cella unitaria e l’aspetto esterno (o abito) non coincidono. CaF2 cristallizza spesso sotto forma di ottaedri.

L’abito è determinato da fattori complessi, chimici e fisici, per lo più di carattere cinetico.

· Come correlare diversi abiti alla simmetria reale del cristallo?

Basta osservare il tipo e numero di elementi di simmetria del cristallo:

· Un cubo ed un ottaedro hanno la stessa simmetria

· Un tetraedro ha minor simmetria

· Tutte e tre le forme posseggono 4 assi ternari inclinati di 109.47°, ovvero appartengono allo stesso sistema cristallino. NaCl e CaF2 sono ambedue cubici (nonostante la diversa morfologia!)

INDICE

Una trasformazione geometrica che porta un oggetto in autocoincidenza è detta operazione di simmetria.

Elemento di simmetria: ente geometrico che permette l’esistenza di operazioni di simmetria.

Es.: un vettore di traslazione reticolare a (elemento di simmetria) permette l’esistenza di operazioni di simmetria caratterizzate dalla traslazione secondo na (n intero, positivo, nullo o negativo).

Se l’operazione di simmetria lascia inalterato almeno un punto, si parla di simmetria puntuale.

Il luogo geometrico (punto, linea o piano) che è inalterato dall’operazione di simmetria coincide con l’elemento di simmetria.

Identità: operazione banale che lascia inalterato un oggetto Simbolo (E)

Piano di Riflessione: lascia inalterato l’oggetto per riflessione normale ad esso. Simbolo = m

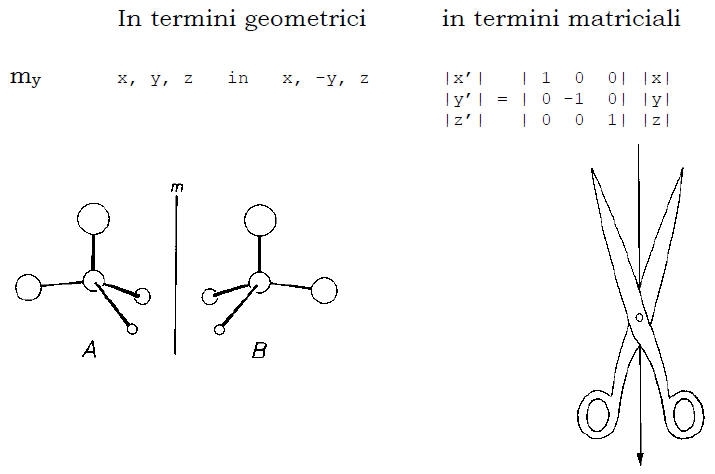
Asse di rotazione: lascia indistinguibile un oggetto dopo rotazione intorno ad esso.

L’ordine dell’asse è dato da X, ove X = 360°/e ed e è il minimo angolo diverso da 0° richiesto per avere autocoincidenza.

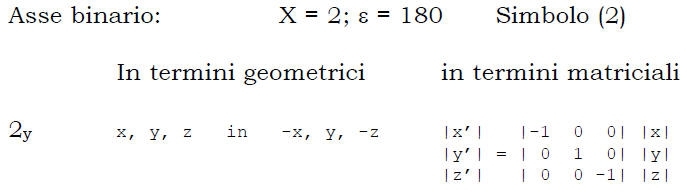
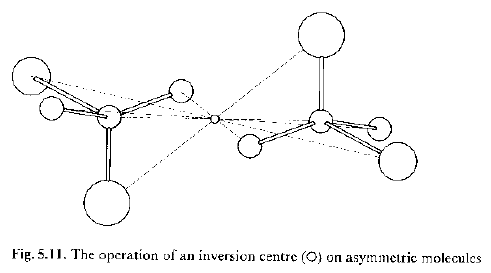
Centro di inversione: correla coppie di punti opposti rispetto ad esso tramite l’operazione di inversione. Simbolo (-1)

Combinazione di operazioni di simmetria (concettualmente, moltiplicazione)

C = A*B significa applicare un’operazione B, poi la A, per ottenere l’operazione C

P.es. Due rotazioni consecutive concordi di 90° generano una rotazione di 180°: 2 = 4 * 4

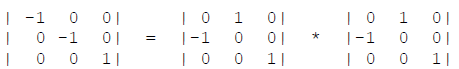
P.es. Due rotazioni consecutive discordi di 90° generano una rotazione di 0°: E = inv(4)*4 oppure E = 4-1 * 4

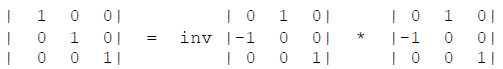
P.es. Una rotazione di 180° seguita da una riflessione attraverso un piano perpendicolare all’asse binario equivale ad una inversione: -1 = my * 2y

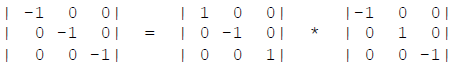
Esistono operazioni di simmetria che concettualmente derivano dalla combinazione di inversioni, riflessioni e rotazioni, ma le cui componenti non sono operazioni di simmetria dell’oggetto: operazioni composte.

Asse di rotoinversione: operazione di simmetria composta generata dall’applicazione successiva di una rotazione (X) ed una inversione (-1).

Simbolo (-X) (-X) = (-1) * X

Assi di rotoinversione

–1: rotazione di 360° + inversione -1 = -1 * 1

–2: rotazione di 180° + inversione -2 = -1 * 2

Quindi –2 = m

–3: rotazione di 120° + inversione -3 = -1 * 3

–4: rotazione di 90° + inversione -4 = -1 * 4

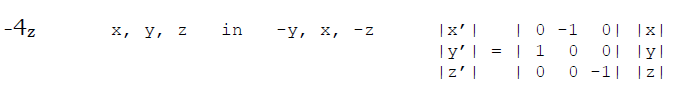
–6: rotazione di 60° + inversione -1 = -1 * 6

–1: rotazione di 360° + inversione -1 = -1 * 1

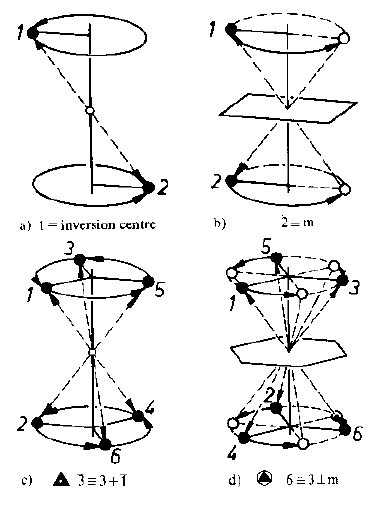
Solo assi di rotoinversione di ordine dispari (-1 e –3) implicano la presenza effettiva di un centro (–1) di inversione.

L’applicazione successiva di due rotoinversioni –4 (attorno allo stesso asse) genera una rotazione di 180° (asse binario).

2z = -4z * -4z

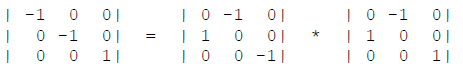
Assi di rotoriflessione: operazioni di simmetria composta generate dall’applicazione successiva di una rotazione intorno ad un asse (X) ed una riflessione nel piano normale ad esso (-2 = m).

Simbolo (Sx) (Sx) = (-2) * X

Le operazioni ad esso associate non sono nuove operazioni di simmetria: infatti si dimostra che:

S1 = m; S2 = -1; S3 = -6; S4 = -4; S6 = -3