Portale "Ingegneria e Campanologia" - Autore - Sommario - Mappa del Sito - Home
Strutturistica Chimica
AREA I - ARTE TECNICO-SCIENTIFICA (ATS)
Cap. ATS-F02 - Chimica - Pag. ATS-F02.09
Gli argomenti trattati sono stati inseriti da Ing. Arch. Michele Cuzzoni nel 2012 - © Copyright 2007- 2025- e sono desunti dalla documentazione indicata in Bibliografia a fondo pagina
Reticoli di Bravais e sistemi cristallini
Come in 2D, anche in 3D si individuano un motivo, che si ripete in modo periodico nello spazio e un reticolo (disposizione di punti, ciascuno che possiede lo stesso intorno per simmetria).
Nello spazio 3D esistono elementi di simmetria traslazionale che non sono possibili in 2D:
· in 2D: linea di scorrimento
· in 3D: piano di scorrimento (glide plane)
· in 3D: asse di rotazione elicogiro (asse screw)
Quindi, la descrizione delle diverse disposizioni possibili sarà più complessa (e non facilmente deducibile come in 2D) Il procedimento logico utilizzato in 2D è comunque lo stesso.
· Ci saranno ‘poliedri di base’ che definiranno delle unità di ripetizione ed il reticolo 3D;
· Ci sarà un numero finito di combinazioni di elementi di simmetria 3D (gruppi spaziali).
Il lavoro sistematico (geometrico) è stato iniziato da Frankenheim (1835) che ha proposto 15 reticoli 3D differenti.
Bravais ha dimostrato (1848) che due di essi erano ‘identici’, analoghi 3D dei reticoli planari a base rombica o a base rettangolare centrata.
I reticoli 3D possibili, indipendenti, sono solo 14!
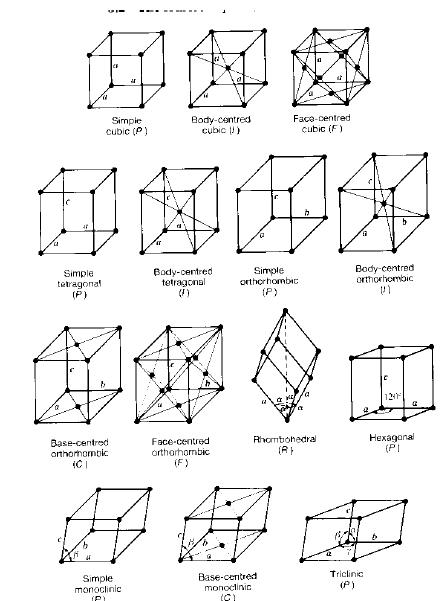
Ogni reticolo è caratterizzato da vettori di base a, b e c.
· Normalmente si indicano le loro lunghezze a, b e c e gli angoli interassiali a, b e g.
· N.B. a è l’angolo opposto ad a, b opposto a b, g opposto a c.
· Tipicamente si usa un sistema di riferimento destrorso, in modo che V = a.(bxc) sia positivo.

Le celle P sono Primitive un punto reticolare per cella unitaria: 8 x 1/8 = 1
Le celle I sono a corpo centrato (Innerzentrierte) due punti reticolari per cella unitaria: 8 x 1/8 + 1 x 1 = 2
Le celle F sono a facce centrate (Face-centered) quattro punti reticolari per cella unitaria: 8 x 1/8 + 6 x ½ = 4
Le celle C sono a base centrata (opposta a c) Due punti reticolari per cella unitaria: 8 x 1/8 + 2 x ½ = 2
Analogamente per basi centrate A e B (due punti reticolari).
I 14 reticoli di Bravais si possono ottenere per impilamento dei diversi (5) reticoli planari:
· Il cubico ed il tetragonale da reticoli planari quadrati P uno sull’altro (P) o sfalsati (di ½, ½, ½ per I; di ½, ½, 0 per F)
· Gli ortorombici P ed I da reticoli planari rettangolari P
· Gli ortorombici C ed F da reticoli planari rettangolari C
· I monoclini e triclini da reticoli planari obliqui (risp. eclissati o parzialmente sfalsati)
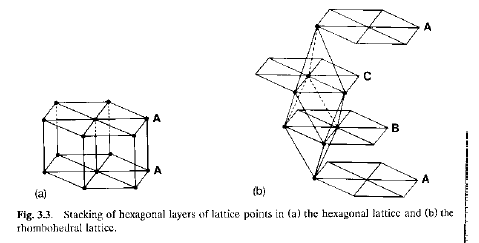
· Il romboedrico e l’esagonale da reticoli planari esagonali (con vettore di traslazione 1/3, 2/3, z o eclissati, risp.)
Sequenza AAA: reticolo esagonale P
Sequenza ABC: reticolo romboedrico
R
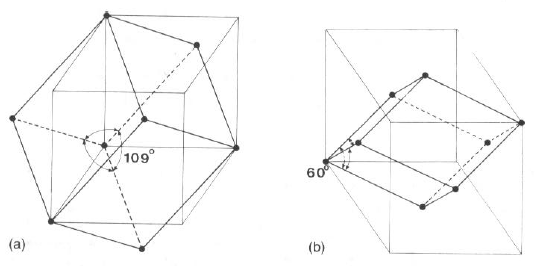
Casi romboedrici speciali:
-
a = 90° reticolo cubico P
-
a
= 60° reticolo cubico
F
-
a
= 109.47° reticolo cubico
I
Perché è equivalente ad un reticolo ortorombico C. (basta rinominare gli assi…)
Perché è equivalente ad un reticolo monoclino C. (basta scambiare a con c)
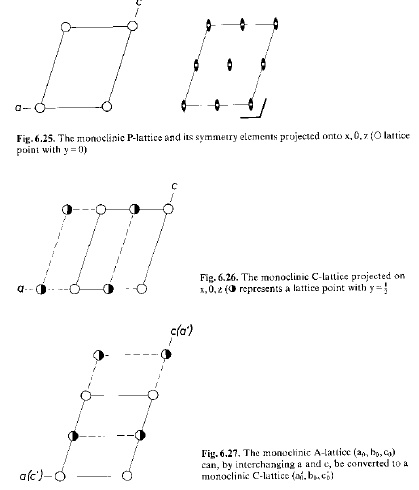
Perché è equivalente ad un reticolo monoclino P di ½ volume. (basta combinare gli assi a e c)
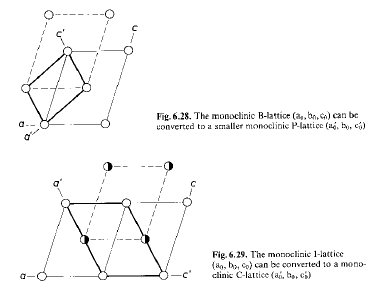
Perché è equivalente ad un reticolo monoclino C. (basta combinare gli assi a e c)
Perché è equivalente ad un reticolo monoclino C di ½ volume
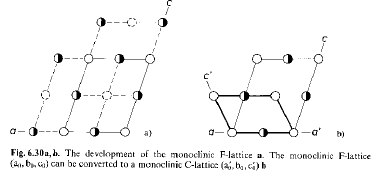
Perché è equivalente ad un reticolo tetragonale I di ½ volume
· Le ‘celle unitarie’ di Bravais sono le ‘molecole integranti’ definite da Haüy.
· Quindi, l’aspetto e la forma macroscopica ‘osservabile’ dei cristalli dipenderà dalla forma e simmetria dei reticoli di Bravais.
· La simmetria di ogni reticolo è una simmetria puntuale, determinata dall’insieme di piani ed assi di simmetria: tale collezione si chiama gruppo di simmetria puntuale.
La (co)presenza e natura di diversi elementi è determinata da regole di mutua compatibilità:
· P.es. due assi binari ortogonali ne generano un terzo ortogonale ad ambedue.
· Esistono regole di autoconsistenza (gruppo matematico). Il gruppo di simmetria puntuale prescinde dalla centratura del reticolo, ovvero i reticoli cubici P, F ed I appartengono alla stesso sistema cristallino. Il concetto (storico) di sistema cristallino è essenzialmente di carattere morfologico e solo secondariamente strutturale.
I 7 sistemi cristallini sono caratterizzati dai diversi raggruppamenti determinati dalla simmetria puntuale dei 14 reticoli di Bravais:
· Cubico, Tetragonale, Ortorombico, Monoclino, Triclino.
· Dal reticolo Esagonale si possono generare due sistemi:
Trigonale ed Esagonale.
· Dal reticolo Romboedrico si genera unicamente un sistema Trigonale; tale reticolo può alternativamente essere descritto da un reticolo Esagonale con centratura R (sistema Trigonale!).
Tutti i reticoli posseggono centri di inversione.
La struttura cristallina potrebbe non averne.
Quindi simmetria del reticolo, sistema cristallino e gruppo di simmetria puntuale possono non coincidere (ma avere relazioni di gruppo-sottogruppo)

Portale "Ingegneria e
Campanologia" -
Autore -
Sommario
- Mappa del Sito -
Home
Bib-TS-081 - Prof. N. Masciocchi - Dispense del Corso di Laurea in Chimica - Insegnamento di strutturistica chimica
Bib-TS-082 - C.Hammond - The Basics of Crystallography and Diffraction - Ed. International Union of Crystallography and Oxford University Press, 240 pg. (Ed. italiana: Zanichelli)
Bib-TS-083 - J.P.Glusker & K.N.Trueblood - Crystal Structure Analysis: A Primer - Oxford University Press, 220 pg. (non tradotto).