I Osservazione: in oggetti che si estendono in una dimensione (fregi e cornici) non sono possibili assi di rotazione altri che binari. Assi ternari, quaternari, etc., generano porzioni dell’oggetto fuori dalla direzione del fregio.

II Osservazione: linee di riflessione con scorrimento possono esistere solo se lo scorrimento è lungo la direzione di riferimento, mai perpendicolari ad essa.

III Osservazione: linee di semplice riflessione possono esistere lungo la direzione assiale (orizzontale) e in direzione normale ad essa (verticale).

Si possono così costruire 7 gruppi monodimensionali, caratterizzati dal periodo di traslazione a, e da elementi di simmetria puntuali (2, m) o combinati (glide g).

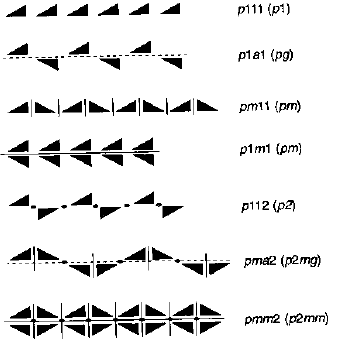
La notazione estesa pxyz significa:

p primitivo (e non può essere altro!)

x simmetria di riflessione relativa all’asse verticale

y simmetria di riflessione relativa all’asse orizzontale

z simmetria rotazionale relativa all’asse verticale

Per 1 si intende nessuna simmetria

Per a si intende glide con traslazione lungo a

Notare che la notazione ridotta cambia l’etichetta a in g; non distingue i due gruppi pm (pm11 e p1m1); riordina i simboli con l’asse binario davanti.

Diagramma di flusso per l’identificazione dei gruppi 1D.

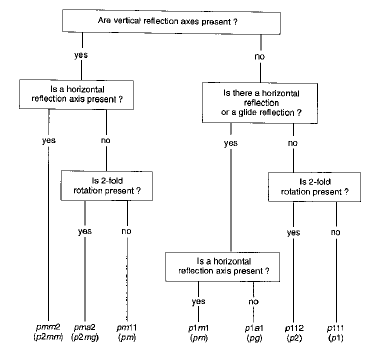
Individuare i gruppi 1D dei seguenti fregi periodici:

INDICE

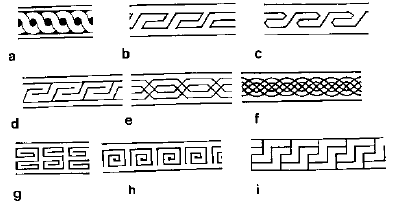
Agli oggetti non si associa solamente una forma (geometria), ma anche una proprietà aggiuntiva (p.es. il colore).

Esempio chimico: oggetti con spin, momento magnetico, etc.

Se questa proprietà ha solo due stati possibili, on e off, up e down, etc., si hanno simmetrie di colore bianco-nero.

Esisterà quindi un nuovo elemento di simmetria: il cambiamento di colore.

Elementi ‘normali’ che cambiano il colore sono indicati con l’apice. 2 diventa 2’; m diventa m’.

2’ è l’elemento di simmetria che ruota l’oggetto di 180° e ne cambia il colore!

m’ è l’elemento di simmetria che riflette l’oggetto e ne cambia il colore.

Schema delle operazioni aggiuntive di simmetria di colore.

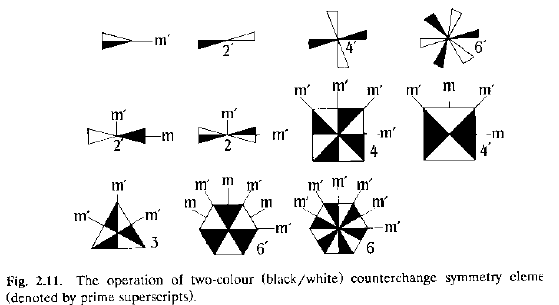
I gruppi monodimensionali sono 7; quelli colorati 10; Tot.: 17

I gruppi planari sono 17; quelli colorati 29, Tot.: 46.