Portale "Ingegneria e Campanologia" - Autore - Sommario - Mappa del Sito - Home
Strutturistica Chimica
AREA I - ARTE TECNICO-SCIENTIFICA (ATS)
Cap. ATS-F02 - Chimica - Pag. ATS-F02.07
Gli argomenti trattati sono stati inseriti da Ing. Arch. Michele Cuzzoni nel 2012 - © Copyright 2007- 2025- e sono desunti dalla documentazione indicata in Bibliografia a fondo pagina
Ricoprimento o tessellazione (problema 2D)
Quesito: Come si può ricoprire un piano con poligoni regolari?
Quesito: Si può ricoprire completamente ed in modo periodico un piano con oggetti senza simmetria?
Come dedurre da un disegno planare periodico il gruppo di simmetria planare corrispondente?
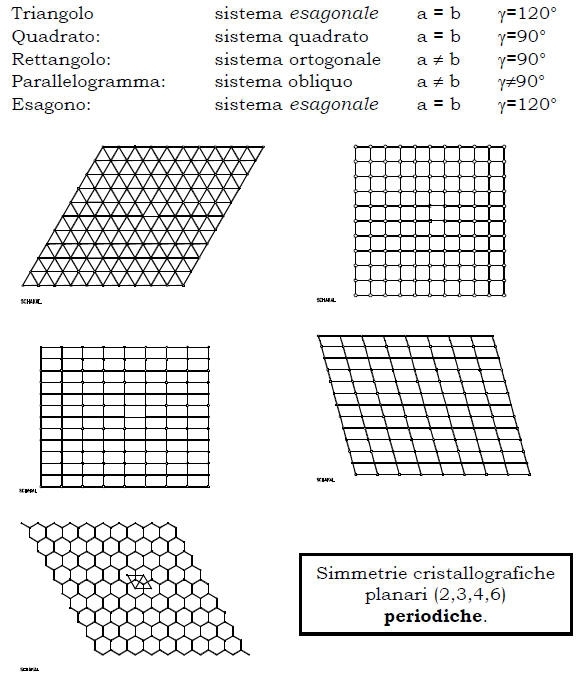
Diversamente, la ricopertura completa del piano non può essere effettuata con: Pentagoni, Eptagoni, Ottagoni, etc., Cerchi (5,7,8,...,¥)
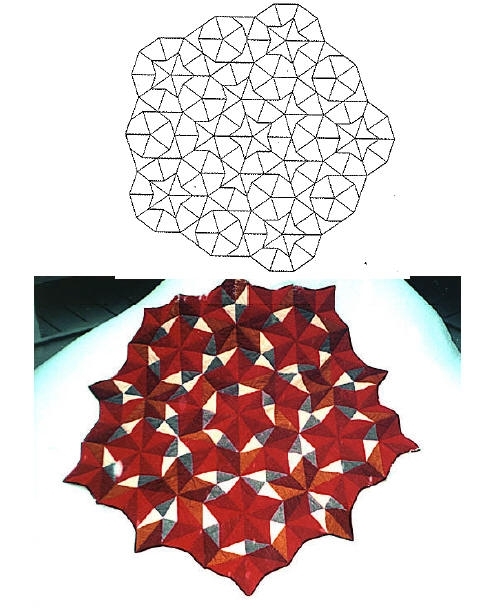
Ricopertura aperiodica con poligoni differenti (Penrose, 1974). Quasi-cristalli (leghe Al-Mn, Schechtman et al., 1951)
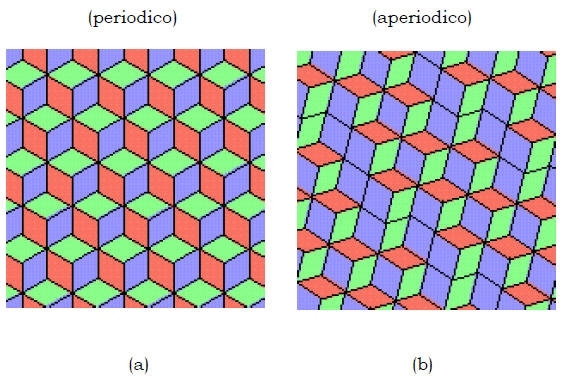
Tessellazione del piano con rombi (2D):
(a) di ugual dimensione (angoli di 60 e 120°)
(b) di dimensione diversa (angoli diversi da 60 e 120°)
Esempio: Studi grafici di M.C.Escher (anni ‘40 e ‘50).
![]() https://www.mcescher.com/
https://www.mcescher.com/


Ciò che importa non è la natura del poligono (la piastrella), ma la forma dell’oggetto e la sua orientazione.
I diversi oggetti sono mutuamente complementari.
Piastrella: idealizzazione geometrica del periodo di ripetizione.
Contenuto della piastrella: oggetto con forma ed orientazione.
Cristallo: Ripetizione periodica di oggetti (dalle forme più disparate), in 1, 2 o 3 dimensioni.
· 1D Periodo (Pettine, Battiti cardiaci)
· 2D Maglia (Favo d’api; Reticella)
· 3D Cella (Carceri, Caselle Postali)
· Prendiamo un punto nel piano (1) e, tramite un asse binario esterno ad esso, generiamo il suo simmetrico (2):
· Applichiamo a (1) una traslazione generica a generando (3)
· Il punto (4) è generato dall’asse binario che opera su (3).
· Il parallelogrammo di lati a e b e angolo interassiale g costituisce la cella unitaria del reticolo planare obliquo.

reticolo planare obliquo simmetria 2 a ¹ b e g ¹ 90°
· Prendiamo un punto nel piano (1) e, tramite un asse binario esterno ad esso, generiamo il suo simmetrico (2):
· Applichiamo a (1) una traslazione a, generando (3), tale che (1),(3),(2) sia un triangolo retto;
· Il punto (4) è generato dall’asse binario che opera su (3).
· Il parallelogrammo di lati a e b e angolo interassiale 90° è un rettangolo ed costituisce la cella unitaria del reticolo planare retto.
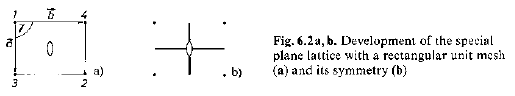
reticolo planare retto simmetria mm a ¹ b, g=90°
· Prendiamo un punto nel piano (1) e, tramite un asse binario esterno ad esso, generiamo il suo simmetrico (2):
· Applichiamo a (1) una traslazione a, generando (3), tale che (1),(3),(2) sia un triangolo isoscele, con i due lati uguali aventi vertice comune in (3);
· Il punto (4) è generato dall’asse binario che opera su (3).
· Il parallelogrammo di lati a e b e angolo interassiale g è un rombo e costituisce la cella unitaria del reticolo planare rombico.
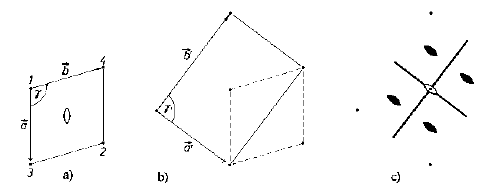
reticolo planare rombico simmetria mm a = b, g¹90°
Nota bene: questo reticolo ha la stessa simmetria del reticolo planare retto: come mai?
E’ possibile trasformare il reticolo planare rombico in un reticolo planare retto non primitivo, ma centrato, combinando a e b in modo che: a’ = a+b e b’ = a-b e g’ = 90°.
· Prendiamo un punto nel piano (1) e, tramite un asse binario esterno ad esso, generiamo il suo simmetrico (2):
· Applichiamo a (1) una traslazione a, generando (3), tale che (1),(3),(2) sia un triangolo isoscele retto;
· Il punto (4) è generato dall’asse binario che opera su (3).
· Il parallelogrammo di lati a e b e angolo interassiale 90° è un quadrato e costituisce la cella unitaria del reticolo planare quadrato.

reticolo planare quadrato simmetria 4m a = b, g=90°
· Prendiamo un punto nel piano (1) e, tramite un asse binario esterno ad esso, generiamo il suo simmetrico (2):
· Applichiamo a (1) una traslazione a, generando (3), tale che (1),(3),(2) sia un triangolo equilatero;
· Il punto (4) è generato dall’asse binario che opera su (3).
· Il parallelogrammo di lati a e b e angolo interassiale 120° è un rombo (somma di due triangoli equilateri adiacenti) ed è la cella unitaria del reticolo planare esagonale.
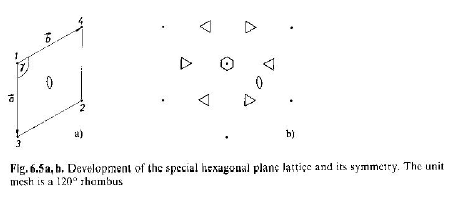
reticolo planare retto simmetria 6m a = b, g=120°

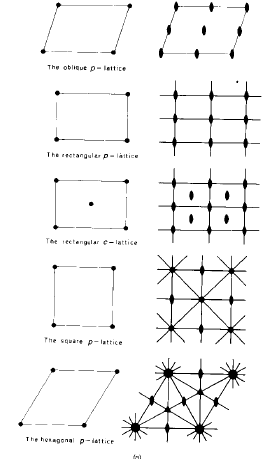
Quesito: perché non esiste un reticolo quadrato centrato? Oppure: perché non esiste un reticolo obliquo centrato?
Gruppi di simmetria planari, non puntuali.
Esistono 10 gruppi puntuali cristallografici.
Esistono 5 reticoli planari.
La combinazione di periodicità di traslazione (simmetria traslazionale) e simmetria puntuale può dar luogo a nuovi elementi di simmetria:
Linee di riflessione con scorrimento: operazione composita che prevede, riflessione su una linea e traslazione lungo di essa di una frazione ben definita (tipicamente metà) cella.
Come le linee di riflessioni normali, cambiano un oggetto nel suo enantiomero, ma, oltre a ciò, lo traslano di ½ parametro.
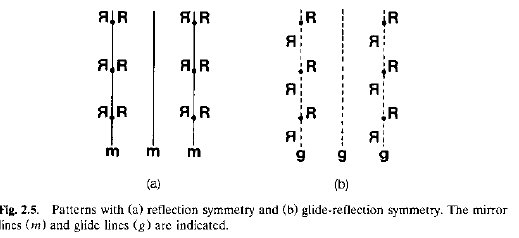
Le linee di riflessione con scorrimento (linee glide, o g) sono compatibili solamente con reticoli planari retti o quadrati.
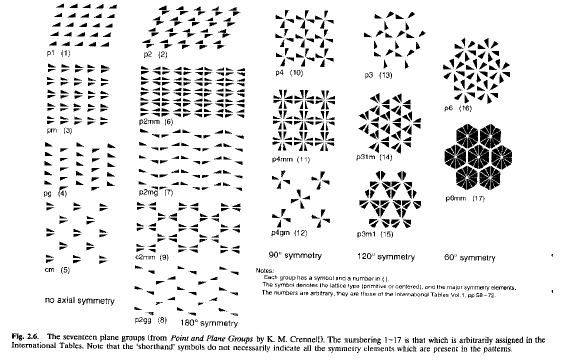
Combinando simmetrie puntuali, reticoli ed eventuali simmetrie composte di scorrimento, si possono ottenere unicamente 17 gruppi planari, ovvero 17 modi diversi di mettere in relazione, in un impaccamento planare, infinito e periodico, un oggetto asimmetrico, come R.
Ogni gruppo planare ha un’etichetta associata:
· p per primitivo, c per centrato;
· si indicano anche gli operatori di simmetria minimali
· (altri possono esserne generati per composizione: p.es. applicare due volte un asse quaternario (90°) genera una rotazione binaria di 180°)

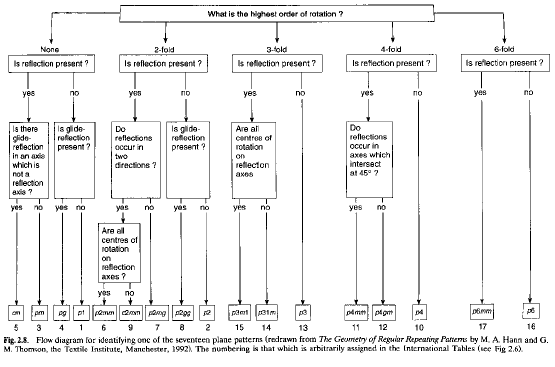
Con un diagramma di flusso del tipo:
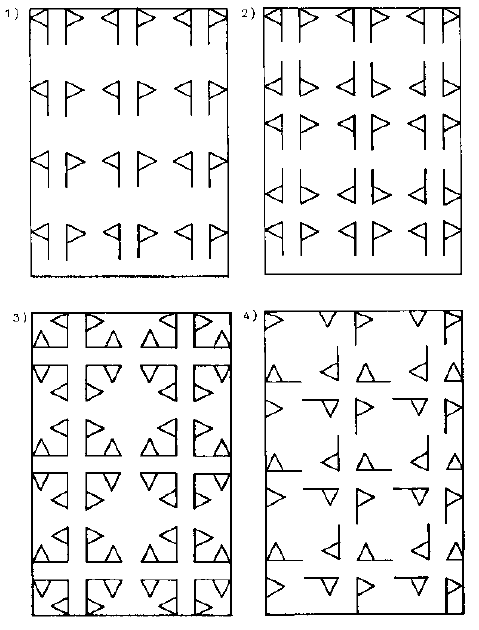
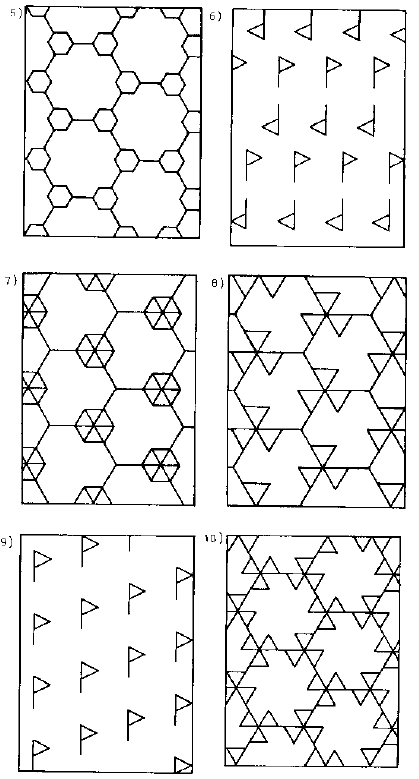
Determinare, per le strutture seguenti, la cella unitaria e gli elementi di simmetria presenti ed il gruppo planare corrispondente.
Portale "Ingegneria e
Campanologia" -
Autore -
Sommario
- Mappa del Sito -
Home
Bib-TS-081 - Prof. N. Masciocchi - Dispense del Corso di Laurea in Chimica - Insegnamento di strutturistica chimica
Bib-TS-082 - C.Hammond - The Basics of Crystallography and Diffraction - Ed. International Union of Crystallography and Oxford University Press, 240 pg. (Ed. italiana: Zanichelli)
Bib-TS-083 - J.P.Glusker & K.N.Trueblood - Crystal Structure Analysis: A Primer - Oxford University Press, 220 pg. (non tradotto).