La descrizione dei tutte le strutture cristalline può avvenire seguendo due processi logici:

· Elencando, caso per caso, ogni struttura, tentando poi di trovare delle analogie (metodo induttivo, tipico del chimico o del metallurgista pragmatico, Tamman e Pope, ca. 1905);

· Analizzando a priori le diverse possibilità di impaccamento molecolare, facendo poi rientrare in ciascuna categoria i diversi casi (metodo deduttivo, tipico del matematico o del teorico analitico, Fedorov e Schönflies, 1891).

Storicamente, è stato più importante la classificazione (Linneana) di Tamman e Pope. Come mai?

· Semplicemente perché i casi noti o prevedibili (poi verificati da Bragg con la diffrazione a raggi X dal 1915 in poi..) erano molto pochi e per niente complessi.

· Dato che, oggi sono note circa 40000 strutture cristalline di composti inorganici (Database ICSD – Karlsruhe) e più di 200.000 strutture cristalline di composti organici ed organometallici (CSD – Cambridge), questo lavoro sarebbe stato impossibile col metodo induttivo.

· L’analisi puramente geometrica di Fedorov e Schönflies permette a tutt’oggi la classificazione ‘semplice’ di questa moltitudine di oggetti cristallini, suddividendole, a ragion veduta, in classi diverse, caratterizzate da diversi elementi di simmetria.

Consideriamo un oggetto piano che non possiede elementi di simmetria: p.es. la lettera R.

R non possiede elementi di simmetria perché non esistono trasformazioni geometriche (operazioni di simmetria) che portano parte dell’oggetto R in autocoincidenza (tranne che per l’operazione identità).

Diversamente, la lettera M contiene due parti uguali, ciascuna delle quali è il riflesso o l’immagine speculare dell’altra. L’elemento di simmetria è una linea di riflessione che biseca, in modo verticale, la lettera M.

In S, che non è una lettera asimmetrica, non esistono linee di riflessione, ma un asse binario perpendicolare al foglio che, per rotazione di 180°, porta i due estremi in autocoincidenza.

INDICE

Linea di riflessione m 2 Linee di riflessione perpendicolari tra loro mm o mm2

Asse di rotazione binario 2 (180°)

Asse di rotazione ternario 3 (120°)

Asse di rotazione ternario + 3 linee di riflessione 3m

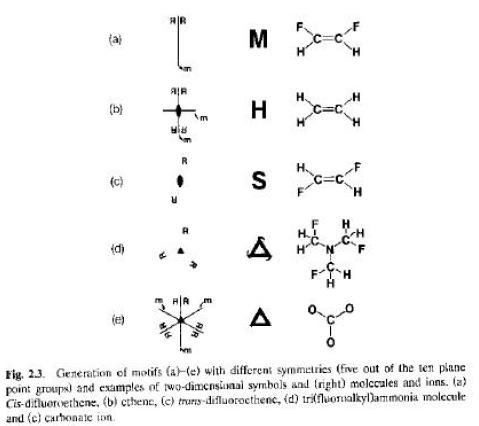
Si chiamano gruppi planari cristallografici i 10 gruppi di simmetria (collezioni di operazioni di simmetria) dalle etichette:

1 (asimmetrico), 2, 3, 4, 6, m, mm, 3m, 4m e 6m.

Esistono infiniti gruppi planari non cristallografici, che hanno operazioni di simmetria di ordine 5, 7 e superiori.

Cosa si intende con cristallografici? Compatibili con la ripetizione periodica per traslazione (vide infra).

INDICE

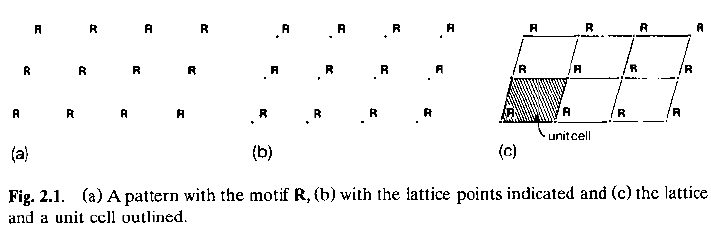
La disposizione regolare nel piano di lettere R (R è il motivo) consiste di una collezione di motivi identici, traslati uno rispetto all’altro, ma equiorientati.

· L’oggetto geometrico responsabile di questa moltiplicazione è il reticolo bidimensionale, caratterizzato da due direzioni di propagazione (ma non da un’origine…).

· La maglia più piccola che identifica tali traslazioni è detta cella elementare o unitaria.

· La convoluzione del motivo col reticolo dà l’oggetto globale (collezione di R).

· L’oggetto globale può essere ottenuto ricoprendo (o tessellando) il piano con celle unitarie traslate secondo i vettori di base della cella stessa.

INDICE

Un reticolo è una disposizione di punti nello spazio (nel piano) che posseggono identico intorno.

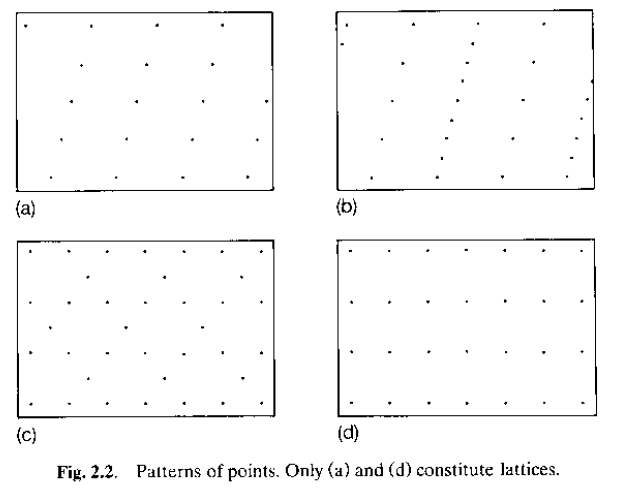
Ogni reticolo planare è caratterizzato da due vettori non paralleli, a e b, di lunghezza a, b ed angolo interassiale g.

a.b = a b cosg

INDICE