Portale "Ingegneria e Campanologia" - Autore - Sommario - Mappa del Sito - Home
Teoria musicale
AREA I - ARTE TECNICO-SCIENTIFICA (ATS)
Cap. ATS-E03 - Musica - Pag. ATS-E03.13
Gli argomenti trattati sono stati inseriti da Ing. Arch. Michele Cuzzoni nel 2009 - © Copyright 2007- 2025- e sono desunti dalla documentazione indicata in Bibliografia a fondo pagina
Se vogliamo effettivamente costruire una scala musicale abbiamo la necessita di misurare l'ampiezza di un intervallo tra due gradi consecutivi della scala. Convenzionalmente il rapporto delle frequenze dei vari gradi di una scala si riferisce al primo grado della scala (chiamato tonica della scala).
Supponiamo per esempio, di avere una scala in cui i rapporti sono indicati in questa tabella (si tratta di una scala pitagorica basata sulla tonica Do).
| rapporto di frequenza rispetto al Do | 1:1 | 9:8 | 81:64 | 4:3 | 3:2 | 27:16 | 243:128 |
|---|---|---|---|---|---|---|---|
| nota | Do | Re | Mi | Fa | Sol | La | Si |
Se vi è necessità di misurare, ad esempio, l'intervallo tra il Sol e il La, cioè il rapporto delle loro frequenze, dobbiamo calcolare:
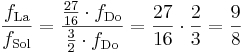
Bisogna convenire che i calcoli non sono sempre agevoli (soprattutto in presenza di rapporti contenenti numeri grandi) ma, soprattutto, non è immediato accorgersi a colpo d'occhio dell'identità di due intervalli.
Ad esempio l'intervallo tra La e Si è esattamente uguale a quello tra Sol e La appena calcolato.
Per ovviare a tale inconveniente, proprio perché nella determinazione dell'ampiezza dell'intervallo gioca un ruolo fondamentale il rapporto, e non la differenza, delle frequenze dei suoni che lo costituiscono, è possibile adottare una scala logaritmica.
Essa si basa sulla divisione dell'ottava in 1200 intervalli uguali, detti cent.
![]()
quindi
![]()
- Perché proprio 1200 parti uguali?
-
-
La scala dei cent si basa sulla nostra moderna scala musicale.
Il vantaggio della scala logaritmica si apprezza quando si debba misurare l'ampiezza di un intervallo costituito da due sottointervalli consecutivi.
La misura in cent dell'intervallo tra due frequenze f1 e f2, è data da
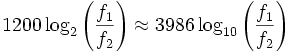 cent.
cent.
Quindi, se il primo intervallo ha misura
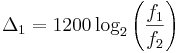 cent
cent
e il secondo intervallo ha misura
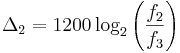 cent
cent
allora l'intervallo ottenuto "raccordando" i due intervalli ha misura
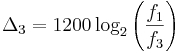 cent.
cent.
Grazie alle proprietà dei logaritmi possiamo allora scrivere
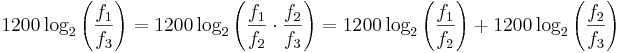
cioè
![]()
Adottando la scala logaritmica l'ampiezza dell'intervallo complessivo è uguale alla somma delle ampiezze dei sottointervalli da cui è costituito.
Ad esempio la scala che abbiamo preso come modello diventa molto semplice se gli intervalli sono espressi in cent:
| rapporto di frequenza rispetto al Do (in cent) | 0 | 204 | 408 | 498 | 702 | 906 | 1110 | 1200 |
|---|---|---|---|---|---|---|---|---|
| nota | Do | Re | Mi | Fa | Sol | La | Si | Do |
Volendo ricalcolare l'ampiezza dell'intervallo Sol-La basta ora effettuare la differenza tra le frequenze di La e Sol.
La coincidenza
degli intervalli dei diversi gradi consecutivi è ora del tutto evidente: sottrarre è molto più facile che dividere! In particolare è immediato riscontrare che in questa scala (è in realtà una scala pitagorica) esistono solo due tipi di intervalli di ampiezza 204 e 90 cent.
Portale "Ingegneria e
Campanologia" -
Autore -
Sommario
- Mappa del Sito -
Home
Bib-TS-069 - Il documento è tratto dal sito fonte originario: http://fisicaondemusica.unimore.it
Licenza Creative Commons: Attribuzione - Non commerciale - Condividi allo stesso modo 2.5 - Italia