Portale "Ingegneria e Campanologia" - Autore - Sommario - Mappa del Sito - Home
Teoria musicale
AREA I - ARTE TECNICO-SCIENTIFICA (ATS)
Cap. ATS-E03 - Musica - Pag. ATS-E03.05
Gli argomenti trattati sono stati inseriti da Ing. Arch. Michele Cuzzoni nel 2009 - © Copyright 2007- 2025- e sono desunti dalla documentazione indicata in Bibliografia a fondo pagina
Definiamo consonante tutto ciò che suona “gradevole” all’orecchio, e viceversa dissonante quel che viene percepito come una sorta di “disturbo” o “tensione” auditiva.
Da un punto di vista storico e culturale, nella tradizione musicale occidentale la dissonanza (prima “praticata” e poi “teorizzata”) nasce tra XV e XVI secolo, come naturale evoluzione del pensiero polifonico, cioè come concetto strettamente legato ad una logica “a più voci”, in quanto si tratta della percezione di una verticalità armonica, che presuppone la contemporaneità di almeno due suoni.
Si avvertì quindi la necessità di inserire, a fine frase, delle Clausole Cadenziali che, in stretta analogia col linguaggio parlato, fungessero da “punteggiatura” (riproponendo, in una sintassi del tutto diversa, i vari punti esclamativi, interrogativi, le virgole, le parentesi e le virgolette su cui è basata la scrittura).
Tali clausole cadenzali erano spesso caratterizzate da una dissonanza che preparasse, con un senso di attesa gravido di aspettative, la risoluzione su un’armonia consonante.
Col tempo questa prassi si è consolidata a tal punto da creare una vera e propria “regia” di tensioni-distensioni armoniche, di aspettative disattese e o prevedibilmente risolte, instaurando un sottile gioco “perverso” con i nervi dell’ascoltatore, ed è un tipo di strategia che potremmo tranquillamente estendere anche ad altri generi artistici come la prosa o la cinematografia.
Tutto questo, naturalmente, funziona alla perfezione all’interno di una logica fortemente ancorata alla tonalità, cioè un pensiero che si è affermato in occidente tra il XVI e il XVII secolo e che imperversa, seppur con qualche incrinatura, ancora ai nostri giorni.
Come si è detto, però, altri tipi di civiltà (pensiamo soltanto alla musica africana o a quella araba o a quella orientale) si muovono in un ambito semantico affatto diverso, e molto lontano dalle dinamiche linguistiche insite nella logica tonale.
Nonostante ciò, esistono delle leggi “universali”, che potremmo estendere ad ogni epoca e cultura in quanto legate alla fisiologia del nostro apparato auditivo, nonché alle proprietà fisiche di ogni corpo vibrante.
Non è un caso, infatti, che praticamente alla base di ogni civiltà vi sia l’intervallo di quinta giusta, cioè la distanza che intercorre tra la seconda e la terza parziale della serie degli armonici; e non è un caso che la sintassi tonale nasca e si sviluppi a partire dalla triade maggiore, formata dalla sovrapposizione delle prime 5-6 parziali armoniche.
Secondo il fisico A. Frova una gerarchia “universalizzabile” di intervalli (dal più consonante al più dissonante), che tenga conto della reazione psicoacustica del nostro orecchio, deve basarsi proprio sulla comparazione delle serie di armonici dei due suoni messi in relazione.
Oggi molti sono gli sforzi di fisici, musicisti ed ingegneri acustici di trovare delle leggi che stabiliscano in maniera inequivocabile tale gerarchia; il problema di fondo, però, che rende vane o quanto meno opinabili molte di queste ricerche, è che il tasso di maggiore o minore consonanza dipende da tanti e tali parametri che sfuggono ad un controllo scientifico da rendere pressoché impossibile (forse fortunatamente!) una qualsivoglia determinazione univoca.
L’armonia, indica la fusione di tre o più suoni (altezze) in un’unica entità musicale, comunemente detta “accordo”.
Frequenze differenti mettono in vibrazione punti diversi della membrana basilare; se tali frequenze sono sufficientemente distanziate (cioè al di fuori della banda critica) il nostro orecchio ha la capacità di distinguere le singole altezze da cui quest’armonia è formata.
Per di più, e questo è un terreno che rimane ancora parzialmente inesplorato, se strumenti diversi eseguono contemporaneamente note differenti, il nostro orecchio ha la magica facoltà di assegnare correttamente le parziali armoniche alle rispettive fondamentali, in modo tale da consentirci di distinguere e separare con esattezza i timbri strumentali.
Anche se, siamo poco educati a riconoscere agglomerati di frequenze e a trattarli alla stregua di veri e propri “impasti” di colori, ogni armonia ha una sua morfologia molto connotata, ed un orecchio ben allenato è in grado di distinguere con facilità una triade maggiore da una minore, un accordo alterato da uno perfetto, un’armonia dissonante da una consonante.
Si tratta, di mettere in relazione secondo un criterio prestabilito diversi aggregati di suoni, in modo da creare un vero e proprio “discorso” di senso compiuto; ed è quello che è riuscito a realizzare, attraverso un processo storico lungo e travagliato, il linguaggio tonale.
La sintassi tonale non è l’unica possibile né tanto meno l’unica esistente, essendo di matrice prettamente occidentale ed essendo scaturita, da specifiche condizioni sociali e culturali; tuttavia è evidente che, avendo “resistito” così a lungo quasi senza subire incrinature, si tratta di un linguaggio particolarmente solido ed efficace, in quanto basato su leggi teoriche ma che ne rispettano a pieno altre di natura psicoacustica.
Fondamentalmente le armonie tonali sono costituite da suoni appartenenti alla serie degli armonici, e pertanto posseggono un solido fondamento “naturale” che ne giustifica anche la gradevolezza percettiva.
Se tale “gradevolezza” può essere considerata universalmente valida, non lo stesso si può dire delle modalità di concatenazione di molteplici entità armoniche, criterio che varia a seconda dell’epoca storica e dell’area geografica d’appartenenza.
La linea guida, che accomuna tutte queste tendenze, è l’aspirazione ad una somiglianza con il linguaggio parlato (e tutte le variazione d’intonazione, dovute anche alla punteggiatura, che lo contraddistinguono) e l’incessante ricerca della tensione verso armonie di carattere chiaramente risolutivo, ed essendo la tensione un parametro eminentemente soggettivo (o quanto meno molto condizionato dall’ambiente socio-culturale in cui viviamo) ogni civiltà ha sviluppato un proprio modo di metterlo in scena.
Nella musica tonale la principale attrazione è costituita dal salto di quarta ascendente (o l’equivalente di quinta discendente) e le relative triadi costruite sulle due note formanti questo intervallo.
Questa semplice concatenazione è detta cadenza perfetta, mentre la successione di più di tre armonie legate dallo stesso grado di attrazione dà vita alla progressione.
Naturalmente la varietà di successioni armoniche è molto vasta, ed è talvolta possibile persino “armonizzare” una stessa melodia in tanti modi diversi.
Per la determinazione della struttura delle diverse scale musicali, hanno giocato un ruolo fondamentale, nelle varie epoche e nelle varie civiltà, più considerazioni di tipo "estetico", dettate dalla pratica musicale e del giudizio di consonanza degli intervalli, che considerazioni ricavate da una reale comprensione del fenomeno sonoro.
Anche l'indagine pitagorica nella quale taluno ha riscontrato una parvenza di "metodo sperimentale" ante litteram, non può dirsi tale in quanto la "sensata esperienza" della ricognizione dei "rapporti semplici" dei suoni consonanti, viene utilizzata per sviluppare un quadro di tipo metafisico (quasi numerologico).
Per uno scienziato moderno di cui Galileo è il paradigma, la scoperta di un legame tra i "rapporti semplici" delle lunghezze delle parti di un monocordo e la consonanza dei due suoni prodotti, una volta stabilito che il suono è un ente fisico, deve avere un'origine connessa alla modalità di produzione e di percezione dei suoni.
Nel seguito del dialogo Galileo dimostra che la lunghezza della corda non può essere l'unico aspetto per "assegnare iuridicamente" l'altezza ad una nota. Con una serie di esperienze egli dimostra che "... Tre sono le maniere con le quali noi possiamo inacutire il tuono (tono) a una corda: l'una è lo scorciarla; l'altra, il tenderla più, o vogliam dir tirarla; il terzo è l'assottigliarla... ".
Nello stesso tempo Galileo sostiene di aver osservato in un bicchiere investito dai "tremori" emessi da un diapason all'ottava un infittirsi della frequenza degli increspamenti osservati: tale osservazione inizia a far pensare a Galileo che l'aspetto determinante per la determinazione dell'altezza del suono sia la frequenza delle oscillazioni.
Egli è tentato, conscio della difficoltà di conteggiare le vibrazioni di una corda oscillante (si pensi che tale numero è dell'ordine di centinaia di vibrazioni al secondo!), di saltare alle conclusioni e di dire che il suono in ottava è dovuto ad un numero di vibrazioni doppio; ma fedele al suo metodo sperimentale egli non può accettare affermazioni che non siano confermate dalle "sensate esperienze". Egli escogita un metodo per "misurare" esattamente il rapporto delle frequenze di due suoni che, ancor oggi, stupisce per la sua ingegnosità.
Uno strumento (musicale), dal punto di vista di un fisico è semplicemente un sistema atto a generare onde sonore ed irradiarle nell'ambiente. In particolare esso si compone (almeno) di:
-
Un elemento vibrante (corda, membrana, lastra, aria) accordabile a diverse frequenze
-
Un risuonatore con la funzione di amplificare la vibrazione e dare una forma all'onda sonora
-
Un adattatore di impedenza tra il sistema vibrante e l'aria circostante
-
-
Le caratteristiche geometriche di tali parti (lunghezza della corda, lunghezza del tubo sonoro, ecc...) determinano la selezione di determinate lunghezze d'onda.
-
La conoscenza delle lunghezze d'onda selezionate non è tuttavia sufficiente a giustificare l'altezza del suono emesso. È necessario a tal scopo, come mirabilmente intuito da Galileo, conoscere la frequenza di oscillazione delle parti vibranti.
Ciò può essere fatto, il calcolo della frequenza del suono emesso richiede anche la conoscenza della velocità con cui l'onda si propaga lungo l'elemento vibrante, secondo la relazione:
Tale velocità dipende da caratteristiche fisiche dell'elemento vibrante; in particolare:
-
nel caso delle corde, dalla tensione della corda (è ciò che variamo quando "accordiamo" una chitarra) e dalla "grossezza" della corda (l'onda viaggia tanto più velocemente quanto più sottile è la corda). Il "mi cantino" della chitarra genera un suono di elevatissima frequenza (molto acuto) in quanto la corda che lo genera è sottile e molto tesa. Quando Galileo parla dei modi per "inacutire il tuono" egli non fa altro di modificare la velocità di propagazione delle onde meccaniche nell'elemento vibrante.
-
nel caso dei tubi sonori (in cui a vibrare sono le particelle d'aria messe in moto dallo strumentista), dalla pressione e dalla densità del fluido contenuto nel tubo sonoro.
Di solito quando si suona uno strumento, lo strumentista genera i suoni desiderati modificando le caratteristiche geometriche dell'elemento vibrante (fanno eccezione gli strumenti a fiato nei quali lo strumentista può selezionare, modificando la pressione del getto d'aria, più note senza modificare la lunghezza del tubo sonoro)
-
il violinista accorcia o allunga la parte di corda vibrante creando con il dito un estremo fisso;
-
il flautista modifica la "lunghezza efficace" del tubo sonoro aprendo o chiudendo determinati fori;
Le caratteristiche fisiche si vuole invece, che rimangano inalterate (in realtà spesso assistiamo a violinisti che ripristinano "al volo" l'accordatura, tramite una regolazione fine della tensione delle corde; la qualità di uno strumento si misura anche dalla sua capacità di mantenere l'accordatura). Nel caso del monocordo ovviamente l'accordatura è stabile (cioè la velocità non cambia almeno per il tempo dell'esecuzione dei due suoni) e quindi
-
Il rapporto tra le frequenze di suoni è completamente determinato dal rapporto delle lunghezze delle parti vibranti che lo generano o, per dirla alla Galileo "...dico che non è la ragion prossima ed immediata delle forme de gl'intervalli musici la lunghezza delle corde, non la tensione, non la grossezza, ma sì bene la proporzione de i numeri delle vibrazioni e percosse dell'onde dell'aria che vanno a ferire il timpano del nostro orecchio, (il grassetto è nostro)
In particolare esistendo una diretta proporzionalità tra lunghezza d'onda e lunghezza della parte vibrante (cioè λ=k l ), possiamo scrivere:
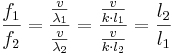
Forte di questo risultato, uno scienziato moderno deve ricercare le ragioni della consonanza nella semplicità dei rapporti tra le frequenze dei suoni emessi.
In un famosissimo passo dei Discorsi intorno a due nuove scienze (1638), Galileo attribuisce l'origine della consonanza al fatto che quando l'orecchio viene investito da due suoni di frequenze commensurabili (secondo rapporti piccoli), esso percepisce una regolarità del fenomeno che si ripete secondo una periodo di breve durata.
In tale passo Galileo rafforza l'argomento con una similitudine meccanica: due pendoli che fossero messi in oscillazione in sincronia e che completassero l'oscillazione in 2 e 3 secondi rispettivamente, in breve (dopo sei secondi, minimo comune multiplo tra due e tre) recupererebbero la sincronia.
Se il rapporto delle frequenze non è commensurabile o comunque il rapporto è espresso da frazioni contenenti numeri elevati (es: 9/8) il recupero della sincronia avviene solo dopo nove pulsazioni della nota più frequente, rendendo l'orecchio incapace di cogliere la regolarità (e quindi la consonanza) del fenomeno complessivo.
Galileo per dar forza alle sue argomentazioni, introduce la famosa similitudine dei pendoli, per spiegare come anche la vista venga confusa dall'osservazione dell'oscillazione di due pendoli che non abbiano frequenze commensurabili secondo rapporti semplici.
La teoria galileiana, benché suggestiva e sapientemente argomentata, si dimostra incompleta per tre ordini di motivi:
-
il primo è che il giudizio di consonanza tra due suoni non dipende solo dal rapporto delle frequenze ma anche dal valore assoluto delle frequenze stesse. Ad esempio negli strumenti ad elevata estensione, un intervallo di terza minore (rapporto 6:5) diventa sempre meno consonante quando si visitano le ragioni più "gravi" (cioè a frequenza minore) della tastiera;
-
il secondo è che nel ragionamento galileiano il suono è caratterizzato da un'unica frequenza (è per dirla in termini moderni un suono puro); in realtà quando una corda vibra (o una campana suona), come si è scoperto dopo Galileo, essa emette un suono composto costituito oltre che dall'onda principale (detta fondamentale - nominale nella campana - che determina la frequenza percepita), da onde (dette parziali) aventi frequenze tutte multiple della frequenza della fondamentale. È ciò una conseguenza del meccanismo di selezione delle lunghezze d'onda;
-
il terzo è di ordine fisiologico: l'attribuire alle regolarità delle vibrazioni del timpano un giudizio di consonanza è evidentemente una forzatura se non si conosce l'elaborazione che di tale vibrazione meccanica viene fatta a livello cerebrale.
Hermann von Helmholtz elabora una teoria della percezione dei suoni che permette, in parte, di superare le tre difficoltà precedenti.
-
Nella regione dei suoni "gravi" i suoni, a parità di rapporto di frequenza, sono molto ravvicinati in frequenza. Von Helmholtz ritiene che suoni molto ravvicinati in frequenza inducano dissonanza perché fanno intervenire fibre nervose molto vicine, generando confusione a livello di elaborazione cerebrale. È questo il fenomeno dei Battimenti descritto dal punto di vista fisiologico.
-
Von Helmoltz attribuisce l'insorgere della dissonanza ai battimenti tra le parziali di ordine superiore se queste cadono all'interno della banda critica. Poiché la larghezza della banda critica va aumentando all'aumentare della frequenza, suoni che hanno un gran contenuto di armoniche di ordine elevato possono rivelarsi autodissonanti.
-
L'intuizione Galileiana che attribuisce la consonanza alla regolarità delle vibrazioni del timpano non è poi, in fondo, molto lontana dal vero, anche nelle spiegazioni più recenti. Suoni, i cui rapporti di frequenza sono espressi da numeri semplici, hanno frequenti coincidenze nelle parziali di ordine superiore (ad esempio la terza armonica del DO è identica alla seconda armonica del SOL, che sta una quinta sopra) ed attivano i medesimi recettori. È come se nella "mappa" delle fibre nervose attivate dal DO fosse contenuta, in parte, anche la "mappa" delle fibre attivate dal SOL. Una conferma di tale fatto si ha nel giudizio di consonanza che attribuiamo a due suoni (ad esempio una quinta) emessi da uno strumento povero di armonici superiori (es. il flauto) e uno strumento ricco di armonici superiori (es. il pianoforte o la campana): nel secondo caso il suono ci appare più armonioso come se la "sincronia" galileiana fosse rafforzata dalla coincidenza delle armoniche superiori.
Non si deve però credere che la teoria di Von Helmholtz offra un criterio oggettivo per stabilire una gerarchia di suoni consonanti. Oggi molti sono gli sforzi di fisici, musicisti ed ingegneri acustici di trovare delle leggi che stabiliscano in maniera inequivocabile tale gerarchia; il problema di fondo, però, che rende vane o quanto meno opinabili molte di queste ricerche, è che il tasso di maggiore o minore consonanza dipende da tanti e tali parametri che sfuggono ad un controllo scientifico (il contesto musicale al quale si fa riferimento, il registro nel quale gli strumenti musicali agiscono, la relazione tra strumenti dal timbro differente, etc.) da rendere pressoché impossibile una qualsivoglia determinazione univoca.
Portale "Ingegneria e
Campanologia" -
Autore -
Sommario
- Mappa del Sito -
Home
Bib-TS-069 - Il documento è tratto dal sito fonte originario: http://fisicaondemusica.unimore.it
Licenza Creative Commons: Attribuzione - Non commerciale - Condividi allo stesso modo 2.5 - Italia