Portale "Ingegneria e Campanologia" - Autore - Sommario - Mappa del Sito - Home
Fisica Acustica
AREA I - ARTE TECNICO-SCIENTIFICA (ATS)
Cap. ATS-E01 - Fisica - Pag. ATS-E01.04
Gli argomenti trattati sono stati inseriti da Ing. Arch. Michele Cuzzoni nel 2008 - © Copyright 2007- 2025- e sono desunti dalla documentazione indicata in Bibliografia a fondo pagina
Velocità di propagazione delle vibrazioni longitudinali
Vogliamo determinare la velocità del suono nei solidi, nell’ipotesi che le onde siano longitudinali. Per circoscrivere il fenomeno, consideriamo un prisma allungato, assumendo queste due ipotesi:
-
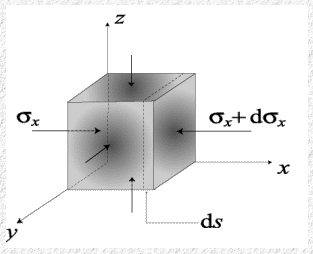
Le onde sonore (onde elastiche) si manifestano come un treno di vibrazioni longitudinali, parallelamente alla direzione di propagazione (direzione dell’asse x del prisma: si veda la figura qui sotto). Dunque le deformazioni sono soltanto longitudinali (tuttavia, come vedremo, il materiale costituente il prisma è sollecitato, oltre che nella direzione principale, Ox, anche nelle due direzioni ortogonali, Oy e Oz). Chiamiamo s (elongazione) l’entità dello spostamento di un punto del materiale, associato alle vibrazioni longitudinali.
Il comportamento del materiale è elastico: in particolare, è definito dal modulo di elasticità a tensione normale E (detto anche modulo di elasticità normale, o modulo di Young) e dal coefficiente di Poisson, cioè dal rapporto fra deformazione elastica trasversale e deformazione longitudinale (ciò è dovuto al fatto un prisma sottoposto a trazione, o compressione – in assenza di azioni laterali di contrasto – subisce una strizione trasversale, o un ingrossamento).
Ciò premesso, tenendo conto dell’ipotesi 1), isoliamo – in seno al materiale che costituisce il prisma – le molecole contenute in un volumetto dV = dx·dy·dz. Nell’immagine qui sotto la faccia verticale sinistra del cubetto i cui lati misurano dx, dy e dz si trova a distanza x dall’origine, mentre quella destra si trova alla distanza x + dx. L’asse x coincide con l’asse del prisma, la sua origine è in un punto qualsiasi.

Quando il prisma è investito da un’onda elastica longitudinale, il volumetto dV è assoggettato a due forze: sx·(dydz), sulla faccia di ascissa x, e (sx + dsx)·dxdz (sulla faccia di ascissa x + dx).
Tenendo conto delle convenzioni di segno si ha:
![]()
![]()
che possiamo anche scrivere:
![]()
Questa è la risultante delle forze agenti sul volumetto dV, che sarà equilibrata dalle forze d’inerzia. Dobbiamo quindi considerare il moto di vibrazione delle molecole interne al volumetto dV e, in particolare, la loro accelerazione.
A causa dell’onda elastica da cui è investito, il volumetto dV subisce una deformazione e, a rigore, la cosiddetta elongazione delle molecole giacenti sulla sezione x, cioè il loro movimento alternativo, lungo la direzione dell’asse x, intorno alla posizione di equilibrio, è diversa da quella delle molecole giacenti sulla sezione x + dx (e di quelle intermedie). Per dx tendente a zero possiamo però assumere che tutte le molecole del volumetto dV si muovano solidalmente (ciò equivale a trascurare gli infinitesimi di ordine superiore).
Scriviamo a questo punto l’equazione di equilibrio per il generico volumetto dV per arrivare, se possibile, a un’equazione del tipo:
![]()
che ci dica qual è la posizione di una generica molecola costituente il prisma, in funzione della sua posizione di riposo x (in assenza di perturbazione sonora) e del tempo t.
L’equazione generica
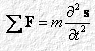
(dove le grandezze in grassetto sono vettoriali) proiettata sull’asse della propagazione del suono fornisce:
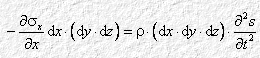
dove r
è la densità del materiale. Si ha allora:
![]()
Le variabili che compaiono in questa equazione sono sx
, x, s e t. Per formulare un’equazione come la (3.1) cerchiamo una relazione tra sx ed s, che ci consenta di sostituire nella (3.2) lo sforzo sx con una sua espressione in funzione di s.
Introduciamo a questo punto l’ipotesi 2), quella di comportamento elastico. Per i dati iniziali del problema, un generico volumetto interno al prisma (che supponiamo di lunghezza indefinita) è soggetto a deformazione soltanto longitudinale: cioè, come abbiamo visto, lungo l’asse x. Dunque ex ¹ 0, mentre ey = ez = 0. Invece gli sforzi assiali sy e sz , agenti sulle facce perpendicolari agli assi y e z, sono in generale diversi da zero. Inoltre gli sforzi agenti su queste facce hanno effetto sulla deformazione lungo l’asse x.
Poiché il volumetto dV è sollecitato in tutte le direzioni, x, y e z, dobbiamo prendere in considerazione tre relazioni di deformabilità, imponendo però che
ey ed ez siano uguali a zero:
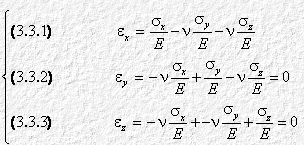
Moltiplichiamo la 3.3.2 per n e confrontiamo il risultato con la 3.3.3. Otteniamo allora:
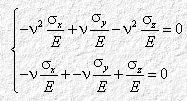
Sommando membro a membro:
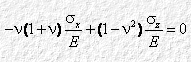
Quindi:
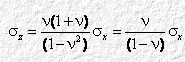
Analogamente:
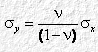
Introducendo i valori di
sz e sy testé ricavati nella 3.3.1 abbiamo la relazione di elasticità complessiva tra sforzi e deformazioni lungo l’asse x:
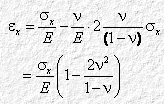
Possiamo anche scrivere:
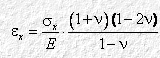
Consideriamo ora che, nel nostro volumetto dV, ex è definito dal rapporto ds/dx, quindi, sostituendo nell’espressione precedente e ordinando i termini:
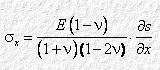
Abbiamo così ricavato una relazione tra sx
ed s, che ci consenta di sostituire nella (3.2) lo sforzo di compressione assiale sx con una sua espressione in funzione di s. Derivando sx rispetto a x otteniamo:
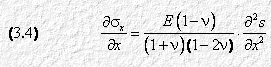
Confrontando la (3.4) con la 3.2) si ha:

Cioè:
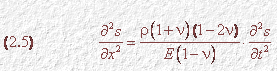
Questa, in generale, è la cosiddetta equazione d’onda: l’equazione differenziale, cioè, che descrive il passaggio di una perturbazione ondosa (longitudinale, in questo caso) in un dato mezzo solido (non fluido) caratterizzato da densità r, modulo di elasticità normale E e coefficiente di Poisson n.
Il significato del fattore:
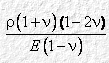
è chiarito dall’analisi dimensionale. Indicando genericamente con l una lunghezza e con t un tempo, si ha:
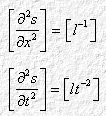
Dunque:
Cioè:

Dunque ha le dimensioni dell’inverso di una velocità. In effetti, si ha:

Portale "Ingegneria e
Campanologia" -
Autore -
Sommario
- Mappa del Sito -
Home
Bib-TS-067 - Ing. Arch. Michele Cuzzoni - Appunti di Fisica 2: Acustica – Facoltà di Ingegneria, Pavia - A.A. 1995-1996
Bib-TS-068 - Il Nuovo Colombo - Manuale dell'Ingegnere - Volume primo - 83^ edizione - Ed. Ulrico Hoepli Milano - 1997 Ristampa 2001