Portale "Ingegneria e Campanologia" - Autore - Sommario - Mappa del Sito - Home
Suono e tono della Campana individuale
AREA I - ARTE TECNICO-SCIENTIFICA (ATS)
Cap. ATS-J02 - Acustica della Campana - Pag. ATS-J02.03
Gli argomenti trattati sono stati inseriti da Ing. Arch. Michele Cuzzoni nel 2012 - © Copyright 2007- 2024 - e sono desunti dalla documentazione indicata in Bibliografia a fondo pagina
Classificazione dei parziali di una campana
|
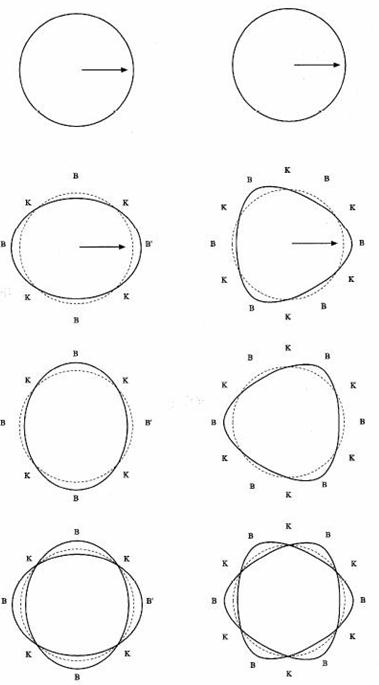
Figura 01: Le modalità di vibrazione orizzontale. |
Quando una campana suona essa oscilla su se’ stessa deformandosi; studi approfonditi dimostrano che le campane hanno moti di vibrazione orizzontali che deformano la campana attraverso due coppie di 6 modi di vibrare: 6 con intensità forte e 6 con intensità debole. Naturalmente l’orecchio percepisce solamente i modi forti. In figura 01 a sinistra, attraverso una rappresentazione in scala esagerata, si mostrano graficamente questi modi di vibrare: data la sezione circolare dalla campana, sottoposta a una percussione indicata dalla freccia. La percussione orizzontale fa’ sì che la campana si allunghi nel verso della freccia (spostamento a destra) e si schiacci nella direzione perpendicolare. Per elasticità del bronzo, dopo aver raggiunto la deformazione massima, la campana torna indietro nella posizione di riposo, poi prosegue la sua corsa nella direzione opposta, raggiunge la massima deformata a sinistra e poi torna di nuovo indietro con minor deformazione e così via finché il suono non si spegne. Il movimento creato va avanti e indietro, parallelamente a ciò che succede in una corda pizzicata o in un pendolo. Questo movimento alternato è proprio del tono fondamentale. All’interno di una campana di tono Do3, la fondamentale vibra con una frequenza di 261,63 Hz, cioè vibra avanti e indietro 262 volte al secondo. Quindi un movimento avanti e indietro impiega 1/262 di secondo, cioè 0,004 secondi per compiersi. Questo è chiamato il periodo di vibrazione. Questo movimento oscillante non è limitato ad un solo punto della campana. Nella seconda immagine a sinistra, che presenta ancora l’oscillazione della fondamentale, si vede che la campana si deforma divenendo un’ellisse. |
I punti B appartengono all’ellisse deformata; i punti K sono invece a riposo.
Quando B’ ritorna alla posizione di riposo (cerchio tratteggiato), B’ prosegue all’interno descrivendo un’ellisse verticale (terza figura).
Nella quarta figura si vedono i 4 movimenti contemporaneamente rispetto alla sezione circolare iniziale di fermo della campana.
Si può chiaramente vedere il comportamento oscillatorio globale dei punti B rispetto ai K che sono sempre fermi nella posizione di riposo.
Il disegno rappresenta il luogo dei punti la cui deformata è massima e quali di essi invece sono sempre fermi a riposo. Questi ultimi si chiamano nodi. Poiché quanto descritto vale per tutte le circonferenze della campana, se ne deduce che il luogo dei punti pulsanti è rappresentato da linee verticali sulla superficie della campana che costituiscono i meridiani dei nodi.
L’aria contenuta all’interno della campana si agita durante la vibrazione. Il suono fondamentale dà la massima vibrazione: nelle grandi campane questo è chiaramente udibile. Al contrario, il suono degli altri parziali lo è di meno, e solo la posizione ravvicinata dell’ascoltatore permette di udirli distintamente. Il fatto notevole è che solo una parte delle armoniche, oltre alla fondamentale producono determinate vibrazioni.
I vari parziali vibrano in modo diverso. Ad esempio la terza minore vibra con 6 ventri e 6 nodi nella circonferenza della campana. Questa deformazione è visibile nella colonna destra di fig. 01.
Le restanti armoniche hanno tipi
di oscillazioni ancora diversi. Per trovarli occorre utilizzare uno degli
strumenti di cui a
![]() pag. J02.02.
In seguito si può esplorare la superficie della campana con lo stetoscopio lungo
tutto il perimetro. Così si possono trovare facilmente tutti i punti di forza
massima e minima.
pag. J02.02.
In seguito si può esplorare la superficie della campana con lo stetoscopio lungo
tutto il perimetro. Così si possono trovare facilmente tutti i punti di forza
massima e minima.
Si usa anche un metodo per la ricerca in direzione verticale, che è più utile. Calcolare la posizione dei ventri e dei nodi nella direzione verticale non è quasi ovvio.
|
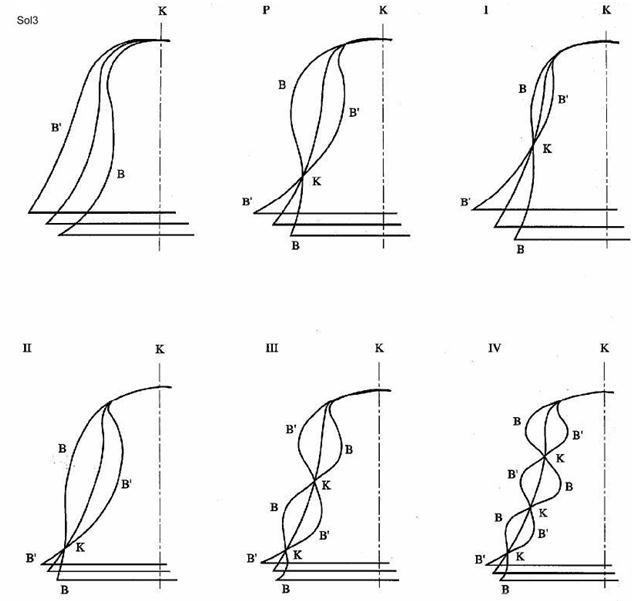
Fig. 02 – Le oscillazioni verticali |
La figura 02 illustra, per un certo numero di armoniche, l’oscillazione della sezione trasversale della campana. La scala di illustrazione è volutamente esagerata per comprendere meglio il fenomeno: per una campana di 500 kg, Sol3, le oscillazioni sono di pochi mm. Si osservano le vibrazioni verticali per questa nota in uno dei meridiani del ventre. Se il numero di meridiani è pari, l’immagine della sezione sinistra è uguale a quello della destra. Quindi la campana si comporta come un diapason nello stesso tono. La parete interna viene deviata verso l’esterno fino al punto B’ (massima posizione). Successivamente la campana ritorna per effetto dell’elasticità e dallo stato di equilibrio si porta ad un’escursione massima verso l’interno denominata B. Anche in questa posizione è possibile avere il disegno della deformata minima, come rappresentato in figura. Il nodo di neutralità si trova nella testa della campana. Se si vuole ottenere un quadro completo del modo in cui la campana vibra per la nota fondamentale, si dovrebbe analizzare il disegno di figura 01 per ogni sezione trasversale ed orizzontale in ogni combinazione del Sol3. Questo gruppo di combinazioni si può solo immaginare, poiché nella realtà questa è un’operazione difficile da fare. La figura spaziale della fondamentale è molto difficile da disegnare, per il primo o per gli armonici superiori è ancora più complicata. |
Lo schema della vibrazione verticale dell’armonico di Prima è rappresentato in figura 02 "P". Dopo l’urto del battaglio la sezione della campana si porta in B’, in mezzo c’è il nodo K, l’altro nodo è ancora nella testa della campana.
Dopo la prima metà del periodo di oscillazione, la forma diventa esattamente il contrario. L’anello di impatto è diretto all’interno e il fianco all’esterno. Si deve rammentare che questo processo, anche se con ampiezza diversa, è presente in ogni sezione verticale della campana con riproduzione casuale. Il nodo K è un punto sulla campana, ed è una linea parallela alla base della campana, quindi anche per i nodi vale una rappresentazione in parallelo.
Nella figura 02 "I" si calcola la terza minore, poi l’ottava, la dodicesima, la doppia ottava e così via. Anche qui si hanno due ventri e un nodo in parallelo, così come il nodo della testa della campana, più punti relativi alla posizione del nodo in qualche altro parallelo.
Lo stesso vale per le vibrazioni di figura II, per la quinta e numerose altre per gli armonici superiori.
La figura III è ancora più complicata. Qui ci sono due famiglie di nodi paralleli, con tutte le conseguenze per i ventri.
Un esempio reale si ha quando l’anello di battuta devia verso l’esterno e la campana assume una forma corrispondente alla linea: B’’ – K X B’’ K X B’’ – K e così via. La figura III vale per l’undicesima e per i parziali più alti. E così si può continuare con ventri supplementari e un nodo in più.
La vibrazione di figura IV è l’ultimo esempio: rappresenta i toni che sono superiori già alla doppia ottava.
Sulla base di queste considerazioni, nella tabella 1 sottostante è data una panoramica di tutti i toni di una campana Do3 qualunque con un diametro di 1556 mm ed un peso di 2310 kg con corona. Per completezza va osservato tuttavia che tra le oltre 40 armoniche registrate, solo una ventina sono le più frequenti.
Questo spettro sonoro comprende armonici diversi rispetto a quelli normalmente trattati, e sono tutti superiori al parziale di ottava, e – fatto che è determinante – sono molto deboli e quindi poco percepite dall’orecchio musicale. Si possono percepire solo in casi eccezionali.
Nella seconda colonna ci sono i soliti nomi propri, nella terza colonna i valori delle variazioni presenti misurate in centesimi rispetto alla visualizzazione normale e nelle ultime colonne un formato che indica a quale tipo di vibrazione verticale corrisponde la figura di oscillazione specifica di quel parziale. Si considera solo mezza oscillazione poiché è la normale prassi in acustica e anche in letteratura.
|
N° |
Nome |
Tono |
Notazione fisica |
||||||
|
1 |
Subbasso |
Do2 |
+ 0 |
I-2 |
|
|
|
|
|
|
2 |
Prima |
Do3 |
-2 |
|
II-2 |
|
|
|
|
|
3 |
Terza minore |
Mib3 |
-1 |
I-3 |
|
|
|
|
|
|
4 |
Quinta |
Sol3 |
+3 |
|
II-3 |
|
|
|
|
|
5 |
Ottava |
Do4 |
-2 |
I-4 |
|
|
|
|
|
|
6 |
Terza maggiore |
Mi4 |
-44 |
|
II-4 |
|
|
|
|
|
7 |
Seconda undicesima |
Fa4 |
-18 |
|
|
III-3 |
|
|
|
|
8 |
Prima undicesima |
Fa4 |
+24 |
|
|
III-2 |
|
|
|
|
9 |
Dodicesima |
Sol4 |
+6 |
I-5 |
|
|
|
|
|
|
10 |
|
La4 |
-41 |
|
|
III-4 |
|
|
|
|
11 |
|
La#4 |
-17 |
|
II-5 |
|
|
|
|
|
12 |
Doppia ottava |
Do5 |
+94 |
I-6 |
|
|
|
|
|
|
13 |
|
Do#5 |
+13 |
|
|
|
IV-2 |
|
|
|
14 |
|
Do#5 |
+40 |
|
|
|
IV-3 |
|
|
|
15 |
|
Do#5 |
+45 |
|
|
|
|
V-2 |
|
|
16 |
|
Re5 |
-43 |
|
|
III-5 |
|
|
|
|
17 |
|
Re#5 |
+6 |
|
|
|
IV-3 |
|
|
|
18 |
|
Re#5 |
+19 |
|
II-6 |
|
|
|
|
|
19 |
|
Mi5 |
-12 |
|
|
|
|
|
VI-2 |
|
20 |
Doppia undicesima |
Fa5 |
+31 |
I-7 |
|
|
|
|
|
|
21 |
|
Fa#5 |
-3 |
|
|
|
IV-5 |
|
|
|
22 |
|
Fa#5 |
+9 |
|
|
III-6 |
|
|
|
|
23 |
|
Sol5 |
+30 |
|
|
|
|
|
VI-3 |
|
24 |
|
Sol5 |
+36 |
|
|
|
|
V-3 |
|
|
25 |
|
Sol#5 |
-14 |
|
II-7 |
|
|
|
|
|
26 |
|
Sol#5 |
+47 |
|
|
|
|
V-4 |
|
|
27 |
|
La5 |
+19 |
I-8 |
|
|
|
|
|
|
28 |
|
La5 |
+32 |
|
|
|
IV-6 |
|
|
|
29 |
|
La#5 |
+11 |
|
|
III-7 |
|
|
|
|
30 |
|
La#5 |
+47 |
|
|
|
|
V-5 |
|
|
31 |
|
Si5 |
+4 |
|
|
|
|
|
VI-4 |
|
32 |
|
Do6 |
-4 |
|
II-8 |
|
|
|
|
|
33 |
Tripla ottava |
Do6 |
+48 |
I-9 |
|
|
|
|
|
|
34 |
|
Do#6 |
-36 |
|
|
|
IV-7 |
|
|
|
35 |
|
Do#6 |
-11 |
|
|
|
|
V-6 |
|
|
36 |
|
Re6 |
-28 |
|
|
III-8 |
|
|
|
|
37 |
|
Re6 |
+27 |
|
|
|
|
|
VI-5 |
|
38 |
|
Re#6 |
+33 |
I-10 |
|
|
|
|
|
|
39 |
|
Mi6 |
-44 |
|
II-9 |
|
|
|
|
Tabella 1: Analisi del suono di una campana Do3, diam. 1556 millimetri, peso 2310 kg
E’ evidente che ci si sofferma di più sulla vibrazione di tipo II. Ci sono molti argomenti convincenti per sostenere che si possono omettere gli armonici superiori. Con tutto ciò, le proprietà fisiche di un parziale sono completamente determinate da due numeri.
IV-6 significa ad esempio che questo parziale è un sovra suono che vibra in una direzione verticale secondo la figura 02-IV e in ogni piano orizzontale il ventre è variato da 12 (doppio di 6 per simmetria) nodi.
Come si approfondiscono le proprietà fisiche della campana, come si deforma quando la campana è eccitata a caso? La risposta pare semplice.
La parete della campana vibra secondo una figura che è la somma di tutte le vibrazioni disegnate nelle figure di Sol3, di Prima, I, II, III, IV, V, VI, VII, VIII, IX, X, XI, e così via, tenendo conto che di volta in vola si deve usare la raffinatezza di scrivere I-2, I-3, ecc. E’ semplice da scrivere, ma difficilmente immaginabile. Soprattutto se ci si rende conto che ogni parziale ha il suo periodo proprio di oscillazione.
Portale "Ingegneria e
Campanologia" -
Autore -
Sommario
- Mappa del Sito -
Home
Bib-TS-000 - Testo di Ing. Arch. Michele Cuzzoni
Bib-TS-246 - André Lehr - Een klankanalyse van de 16de-eeuwse Van Wou-klokken in de Domtoren te Utrecht (Asten, 1980)
Bib-TS-247 - André Lehr - Partial Groups in the Bell Sound. In: The Journal of the Acoustical Society of America , vol.79, 1986, blz.2000-2011
Bib-TS-248 - André Lehr - The designing of swinging bells and carillon bells in the past and present (Asten, 1987)
Bib-TS-249 - André Lehr - The tuning of the Bells of Marquis Yi. In: Acustica , vol.67, 1988, blz.144-148
Bib-TS-250 - André Lehr - A statistical investigation of historical swinging bells in West Europe. In: Acustica , vol.74, 1991, blz.97-108
Bib-TS-251 - André Lehr - Profielconstructies van luid- en beiaardklokken in het verleden (Asten, 1991)
Bib-TS-252 - André Lehr - Acoustic research. In: 45 Years of Dutch Carillons 1945-1990 , L.Boogert, A.Lehr, J.Maassen (ed.), 1992, blz.132-145
Bib-TS-253 - André Lehr - Vormoptimalisatie van luid- en beiaardklokken. In: Symposium Structural Optimization in the Netherlands , F. van Keulen en A.J.G. Schoofs (ed.), November 9, 1995, Technische Universiteit Delft
Bib-TS-254 - André Lehr - Berekening van het klokprofiel. De eindige-elementen-methode in combinatie met optimalisatie-techniek helpt een oud ambacht. In: Principieel, werktuigbouwkundig magazine, Universiteit Twente , jg.1, Lente 1997, blz.23-28
Bib-TS-255 - André Lehr - Designing Chimes and Carillons in History. In: Acustica, 1997, vol.83, blz.320-336
Bib-TS-256 - André Lehr - Metaalkunde en Torenklokken. In: Metalen in Monumenten en Vernieuwbouw , Syllabus van de Studiedag van WTA, Nederland-Vlaanderen, Wetenschappelijk-Technische Groep voor Aanbevelingen inzake Bouwrenovatie en Monumentenzorg, op 21 november 1997 in het Provinciehuis te Antwerpen, blz.60-73
Bib-TS-257 - André Lehr - Campanologie. Een leerboek over klank en toon van klokken en beiaarden (Mechelen, 1997, 2de druk 1998)
Bib-TS-258 - André Lehr - The Geometrical Limits of the Carillon Bell. In: Acustica, vol.86, 2000, blz.543-549
Bib-TS-259 - André Lehr - The Removal of Warbles or Beats in the Sound of a Bell. In: Acustica , vol.86, 2000, blz.550-556
Bib-TS-260 - André Lehr - Geschiedenis van de campanologie (Asten, 2001)
Bib-TS-261 - André Lehr - Leerboek der Campanologie, 2007