Portale "Ingegneria e Campanologia" - Autore - Sommario - Mappa del Sito - Home
Principi generali di analisi acustica
AREA I - ARTE TECNICO-SCIENTIFICA (ATS)
Cap. ATS-J01 - Acustica - Pag. ATS-J01.02
Gli argomenti trattati sono stati inseriti da Ing. Arch. Michele Cuzzoni nel 2009 - © Copyright 2007- 2024 - e sono desunti dalla documentazione indicata in Bibliografia a fondo pagina
Spettri di Frequenza
Lo spettro di un segnale complesso è rappresentato da un grafico con la frequenza di ciascuna componente sull’asse delle ascisse e il corrispondente livello di intensità (o di pressione acustica) sull’asse delle ordinate.
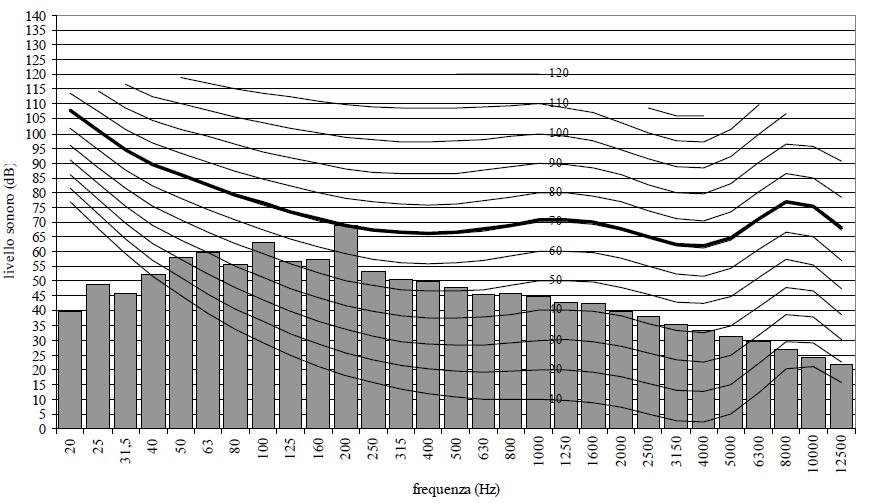
Fig. A - Esempio di spettro di suono complesso
Si riportano di seguito alcuni tipi di spettro:
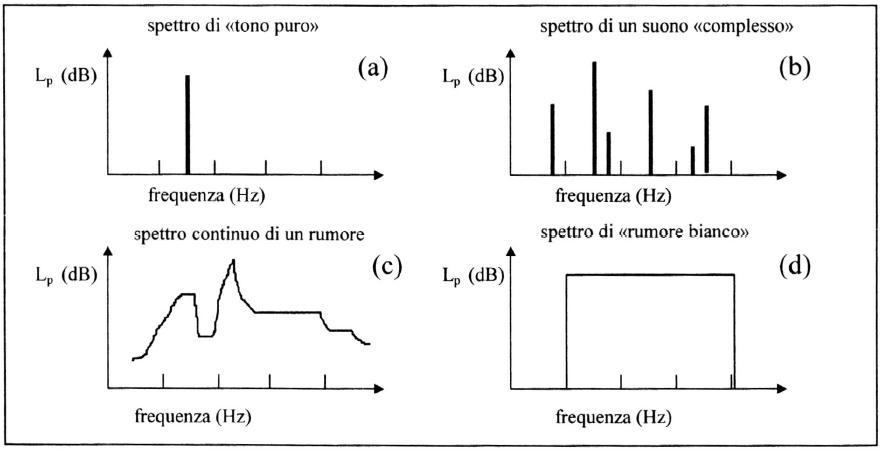
Fig. B - Esempi di spettri sonori
Il calcolo della serie di Fourier permette, di trasformare una tabella di dati, che rappresentano l’informazione del segnale campionato nel tempo, in una diversa tabella di dati che rappresentano il contenuto armonico del segnale.
Quest'ultima tabella è rappresentabile in forme grafiche che prendono il nome di spettri di frequenza. Data la possibilità di esprimere in modi diversi l’informazione sul contenuto armonico, nella letteratura tecnica non vi è purtroppo una rappresentazione uniforme e universalmente accettata di tali grafici, per cui può esserne difficile l’interpretazione.
Si possono comunque ridurre a tre i principali tipi di rappresentazione degli spettri di frequenza relativi ad un segnale periodico.
- Spettro delle componenti immaginarie e spettro delle componenti reali.
In questo caso nel primo grafico vengono riportate sull’asse orizzontale la frequenza delle armoniche considerate (posto a 1 la fondamentale) e sull’asse verticale i coefficienti Ak , cioè l’ampiezza dei seni delle singole armoniche.
Poiché nella rappresentazione complessa queste costituiscono la parte immaginaria, questo spettro è indicato come immaginario.
Un secondo grafico dello stesso tipo riporta invece la parte reale, cioè i coefficienti Bk del coseno, più il coefficiente C per k=0.
- Spettro del modulo relativo a ciascuna armonica e spettro delle fasi iniziali.
- Spettro componenti vettoriali rotanti in senso opposto e spettro delle fasi.
Ogni armonica può essere vista come la proiezione della somma di due vettori ruotanti sincronicamente in senso opposto, ognuno di ampiezza Mk/2.
In questo caso il diagramma completo dovrebbe comprendere anche la parte delle armoniche negative (nel senso di frequenze derivanti dalla rotazione oraria del vettore), ma questa può essere omessa essendo ovviamente simmetrica alla parte positiva, rispetto alla frequenza ‘zero’.
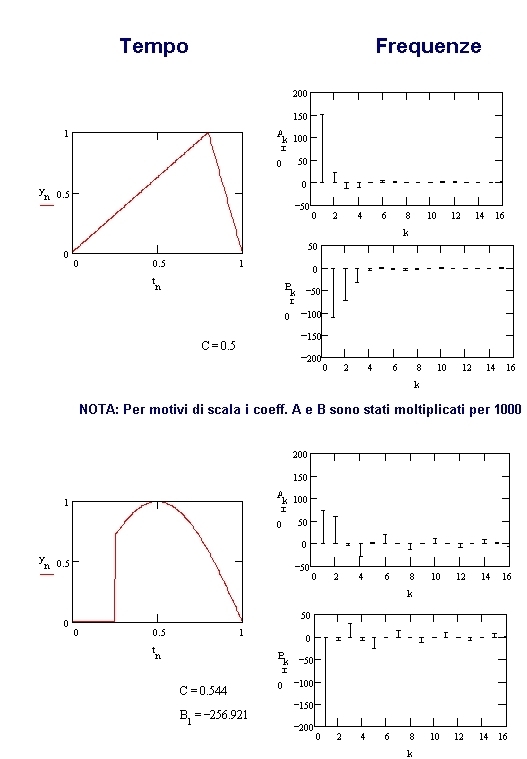
Fig. 01 - Esempi di corrispondenza fra rappresentazioni di segnali nel tempo e con spettri di frequenza immaginario e reale
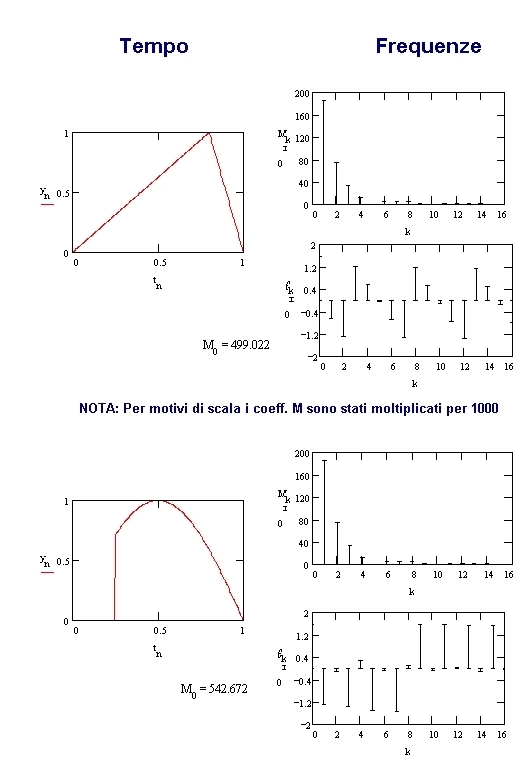
Fig. 02 - Esempi di corrispondenza fra rappresentazioni di segnali nel tempo e con spettri di frequenza a modulo e fase.
Dal punto di vista strettamente matematico, la trasformazione di Fourier di una forma d'onda y(t) di periodo P in una serie di armoniche può essere vista come la soluzione dell'equazione:
y(t) = m 0 + S (m n · e j n w t + m -n · e -j n w t)
dove
w=2· p / P , quindi una costante che rappresenta la pulsazione (rad/sec) dell’armonica fondamentale,
mn è il modulo di un vettore nel piano complesso ruotante alla velocità n· w,
m-n è il vettore coniugato ruotante alla velocità -n·w , cioè in senso opposto.
Il problema consiste quindi nel ricavare la serie mn (con n compreso fra -¥ e +¥) che soddisfa questa uguaglianza .
L’artificio matematico che consente la soluzione è di moltiplicare entrambi i membri per e- j·k· w·t e di integrarli nel tempo per il periodo P.
Fra le forme d’onda trasformabili in spettri di frequenza rivestono particolare importanza gli impulsi rettangolari.
Questi permettono anche di comprendere meglio il significato fisico del contenuto armonico. Se infatti è ovvio che un segnale perfettamente sinusoidale ha come spettro un solo segmento (l’ampiezza del segnale stesso in corrispondenza della fondamentale), è intuibile che un segnale perfettamente rettangolare abbia una serie infinita di armoniche.
La suddivisione del periodo in N intervalli di campionamento influisce però sulla forma dell’impulso e ne limita anche il contenuto armonico.
Nell’esempio, in cui N=128 , l’impulso ha una forma trapezia, con tempi di salita e di discesa di 1/128 del periodo.
Dall’analisi di Fourier si è visto che il numero K di armoniche ricavabili è uguale a N/2 - 1 , quindi in questo caso oltre alla componente continua si possono calcolare al massimo 63 armoniche. Aumentando N si ha una sempre maggiore approssimazione all’impulso rettangolare, con un conseguente incremento del numero di armoniche.
L’ampiezza, o modulo, di ciascuna armonica è rappresentabile nello spettro di frequenza, riportato nel secondo grafico della stessa immagine. E’ interessante notare come varia la forma di questo spettro al variare della durata dell’impulso rispetto al periodo.
La figura successiva rappresenta il caso di un impulso di durata doppia e la terza figura di durata quadrupla di quello iniziale. Si nota che lo spettro tende a concentrarsi verso lo zero, aumentando i moduli delle frequenze più basse e diminuendo quelli delle frequenze più alte (attenzione alla variazione delle scale verticali).
Per approfondire questo argomento si può utilizzare un impulso di area unitaria cioè di durata T e di ampiezza 1/T.
Supponendo inoltre che il periodo sia infinito (considerando così un solo impulso anziché una serie di impulsi), si può applicare il metodo d’integrazione osservando che il segnale y(t) in questo caso ha ampiezza zero fra - ¥ e - T/2, ampiezza 1/T fra - T/2 e + T/2, e ancora ampiezza zero fra + T/2 e + ¥.
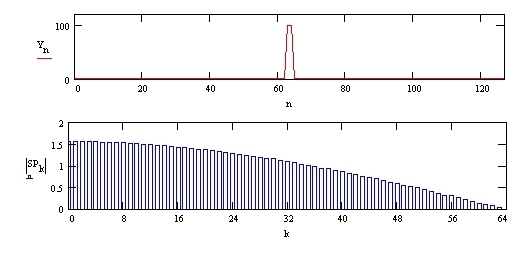
Fig. 03 - Spettro di frequenza (solo modulo) di un impulso di durata2·DT.
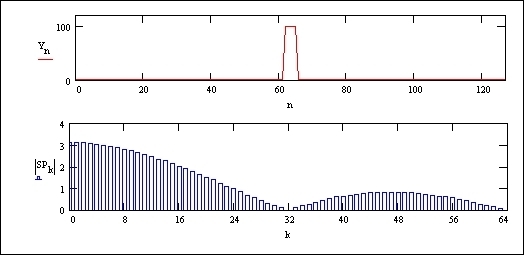
Fig. 04 - Spettro di frequenza nel caso di impulso di durata4·DT
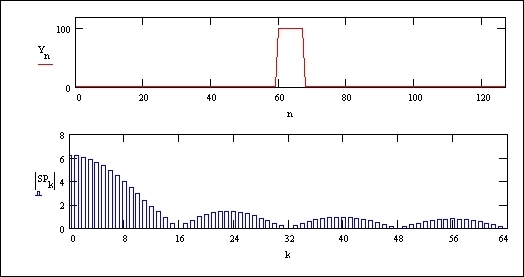
Fig. 05 - Spettro di frequenza nel caso di impulso di durata 8·DT
Ricorrendo alla formula di Eulero, il risultato può essere espresso in forma trigonometrica anziché esponenziale:
sen (w·T/2) | ||
|
G(jw) |
= |
------------ |
|
w·T/2 |
La figura seguente rappresenta appunto la variazione degli spettri continui G (jw) al variare della durata T dell’impulso di area unitaria. Gli spettri sono stati limitati nei grafici fra -1.6 Hz a +1.6 Hz, ma la loro estensione va da - ¥ a+ ¥.
Estrapolando i risultati si possono ricavare due importanti osservazioni:
- Se la durata dell’impulso tende all’infinito (e quindi la sua ampiezza tende a zero) si ha uno spettro costituito da un solo segmento, di ampiezza 1, in corrispondenza della frequenza ‘zero’. Infatti il segnale è in questo caso ‘ continuo ’, senza alcuna armonica.
- Se viceversa la durata dell’impulso tende a zero (e la sua ampiezza all’infinito), si ha uno spettro uniforme, di ampiezza 1, per qualsiasi armonica da- ¥ a+ ¥. Quest’ultimo caso rappresenta la funzione d o di Dirac (perché utilizzata da Dirac nella meccanica quantistica).
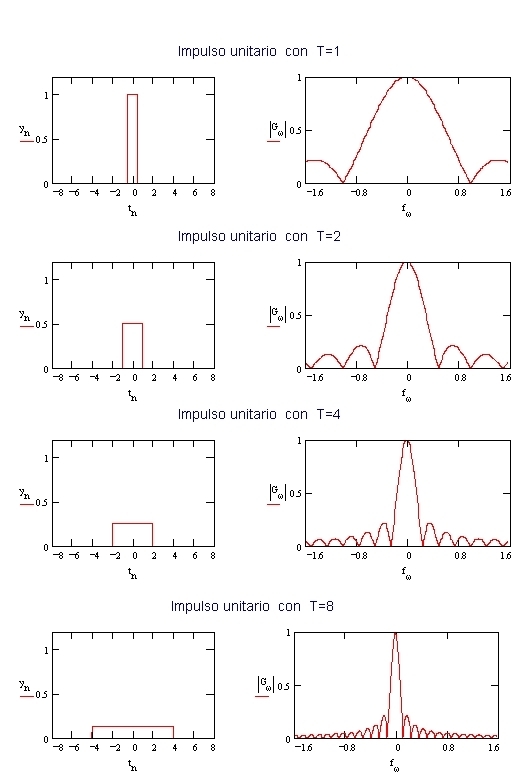
Fig. 06 - Esempi di spettri continui di impulsi unitari di varia durata
Portale "Ingegneria e
Campanologia" -
Autore -
Sommario
- Mappa del Sito -
Home
Bib-TS-067 - Ing. Arch. Michele Cuzzoni - Appunti di Fisica 2: Acustica – Facoltà di Ingegneria, Pavia - A.A. 1995-1996
Bib-TS-068 - Il Nuovo Colombo - Manuale dell'Ingegnere - Volume primo - 83^ edizione - Ed. Ulrico Hoepli Milano - 1997 Ristampa 2001