Portale "Ingegneria e Campanologia" - Autore - Sommario - Mappa del Sito - Home
Meccanica del mezzo continuo e dei
materiali
AREA I - ARTE TECNICO-SCIENTIFICA (ATS)
Cap. ATS-H01 - Meccanica - Pag. ATS-H01.15
Gli argomenti trattati sono stati inseriti da Ing. Arch. Michele Cuzzoni nel 2008 - © Copyright 2007- 2024 - e sono desunti dalla documentazione indicata in Bibliografia a fondo pagina
Lo studio del comportamento meccanico di un metallo o di una lega può essere effettuato tramite appositi test dove un campione di materiale viene montato su una macchina di prova e caricato sino a rottura. L’analisi qualitativa e quantitativa della deformazione del provino e uno studio delle caratteristiche di frattura permettono al progettista di prevedere indicativamente quale sarà la risposta meccanica del materiale ad un determinato tipo di sforzo.
La valutazione di tale comportamento richiede inoltre un’analisi di tutte le variabili che possono influenzare i dati sperimentali, come ad esempio le modalità con cui viene condotta la prova (rapidità, temperatura etc.) e le caratteristiche intrinseche del materiale. In questo capitolo si focalizzerà l’attenzione sulla risposta dei materiali metallici ad uno sforzo di trazione.
La prova di trazione consiste nel sottoporre un provino (figura 1.1) ad una deformazione tramite un carico di trazione unidirezionale applicato ortogonalmente alla sezione del provino stesso. Durante il test il carico viene registrato in funzione della deformazione della sezione di prova (o gage section) del campione. I dati ricavati vengono poi elaborati per costruire la cosiddetta curva tensioni–deformazioni.
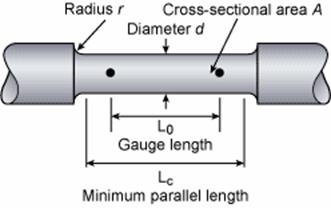
Esempio di provino per prova di trazione
I risultati di una prova di trazione potrebbero essere riportati in una curva carico–allungamento ma in tal modo verrebbero influenzati notevolmente dalla geometria del provino. Per questo motivo si costruisce una curva tensioni–deformazioni, che presenta il medesimo andamento della prima ma che risulta virtualmente indipendente dalle dimensioni del campione.
La tensione nominale s è così definita:
s = F / A0
Dove F è il carico e A0 è l’area iniziale della sezione di prova.
La deformazione nominale :
e = DL / L0
Dove L0 è la lunghezza iniziale della sezione di prova e DL è la variazione di lunghezza.
Tipicamente la curva ha l’andamento descritto in figura:
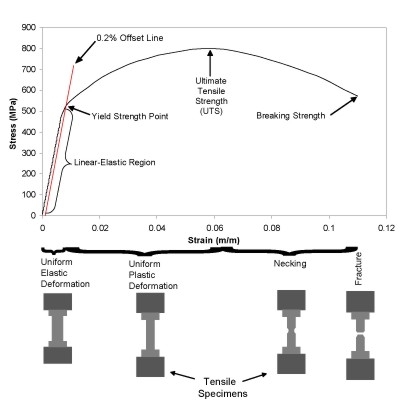
Curva tensione-deformazione nominale
Nella parte iniziale della curva, la regione elastica, tipicamente la tensione risulta linearmente proporzionale alla deformazione. In questa zona i carichi non sono sufficienti a deformare irreversibilmente il materiale e si parla di deformazione elastica.
Quando la tensione supera un determinato valore, detto di snervamento, si osserva una plasticizzazione del provino: in altre parole si sviluppano delle deformazioni che permangono anche dopo la rimozione del carico.
La tensione necessaria per continuare ad allungare plasticamente il provino cresce con il crescere della deformazione plastica: si parla di incrudimento del materiale.
Durante la deformazione plastica il volume del provino rimane pressoché invariato, si assiste allora ad una riduzione uniforme della sua sezione lungo il proprio asse. Inizialmente l’incrudimento prevale sulla riduzione di area e la tensione nominale continua a crescere con la deformazione.
Si giunge infine ad un punto in cui il fenomeno si inverte, l’effetto dell’incrudimento non compensa più la riduzione di area e si ha una localizzazione delle tensioni nella sezione più debole del campione,definita come strizione. Il carico richiesto per deformare il provino inizia allora a decadere sino alla rottura del pezzo.
L’andamento della curva tensioni–deformazioni di un materiale metallico dipende fortemente dalla composizione del materiale, dalla sua storia deformativa e dalle condizioni in cui viene condotta la prova, come ad esempio la rapidità deformativa imposta o la temperatura.
I parametri generalmente usati per descrivere tale curva sono la resistenza a trazione, la tensione di snervamento, l’allungamento percentuale e la riduzione di area resistente. I primi due parametri sono correlati con la resistenza meccanica mentre gli ultimi due danno una misura della duttilità.
Nel caso particolare di una campana, questi effetti si vedono nei punti di battuta: l'azione puntuale è di compressione normale al bordo e di trazione (a destra e sinistra) sotto di esso.
Considerando invece il vaso della campana, l'azione di percussione (avanti e indietro - figura sottostante) del battaglio esercita un'azione di trazione normale al piano della campana sezionata verticalmente (piano con cornice rossa in figura). Il presente ragionamento si basa sulla Teoria del Tensore delle forze e delle deformazioni (Scienza delle Costruzioni).
La linea teorica perfetta di frattura coincide con la sezione colorata in azzurro. In realtà l'andamento delle frattura è molto più elaborato dovendosi considerare numerosi fattori atmosferici, climatici, meccanici (dinamica del battaglio sul bronzo) ed anche storici (presenza di eventuali girature), ecc.
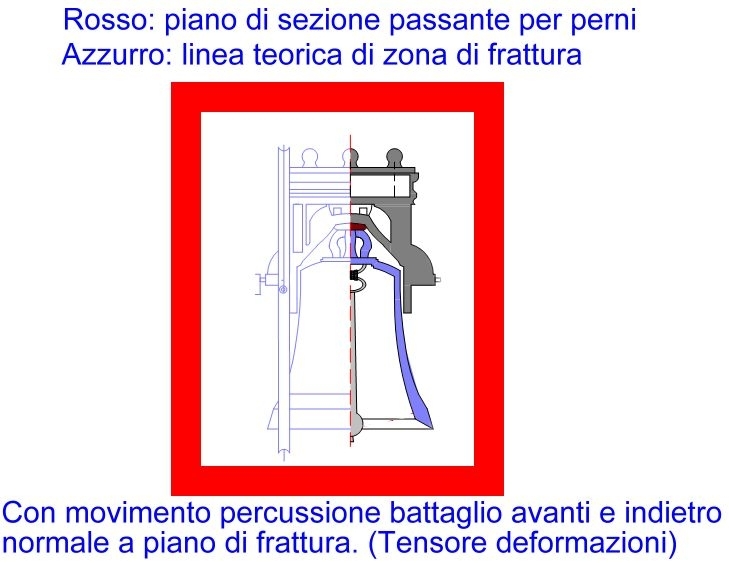
Disegno realizzato da Ing. Arch. Michele Cuzzoni
Quando un materiale metallico viene sottoposto a tensioni relativamente basse i legami atomici vengono messi in trazione. Una volta rimosso il carico i legami si rilassano e il materiale recupera la sua forma originale: si parla di deformazione in campo elastico.
Per molti materiali esiste,nella regione elastica, una relazione di proporzionalità tra tensione e deformazione, relazione descritta dalla legge di Hooke
s = Ee.
Ne risulta che la parte iniziale della curva (s - e) è lineare. Pur non essendo determinato tramite la prova di trazione, il modulo elastico E, (modulo di Young), si può stimare come la pendenza iniziale della curva :
E = s / e
Nella regione elastica un altro parametro può essere calcolato: è il modulo di Poisson u, che quantifica il fenomeno della contrazione laterale:
u = - ( eU) / ( eC)
ove eC e eU rappresentano le deformazioni rispettivamente nella direzione del carico ed in quella perpendicolare.
Il modulo di Young è determinato dalle forze dei legami interatomici nel reticolo metallico e risulta quindi una proprietà intrinseca del materiale. In genere può essere modificato dalla presenza di elementi di lega e da trattamenti termici o meccanici.
Molte strutture ingegneristiche vengono progettate per lavorare in campo elastico nelle normali condizioni di funzionamento. I carichi di lavoro producono deflessioni elastiche reversibili nel materiale e l’ampiezza di tali deflessioni dipende essenzialmente dal modulo elastico. La capacità di un materiale di resistere ad una deformazione elastica è definita rigidità e il modulo E ne è una misura.
Il valore di E per gli acciai risulta più grande che per la maggior parte dei metalli, di conseguenza l’acciaio viene usato diffusamente in condizioni in cui è richiesta una buona rigidità.
Come già sottolineato l’equazione che definisce il modulo di Young, s = Ee, si basa sull’ osservazione che la tensione risulta proporzionale alla deformazione. Tuttavia quando un materiale è soggetto a carichi ciclici o a vibrazioni può deviare dalla linearità anche in campo elastico. Una misura di tale deviazione è la risposta anelastica del materiale.
L’anelasticità è definita come una deformazione completamente reversibile ma dipendente dal tempo.
Tale dipendenza deriva dalla mancanza di movimenti atomici istantanei durante l‘applicazione del carico. I meccanismi che provocano questo ritardo di risposta da parte del materiale possono includere fenomeni diffusivi degli elementi leganti o delle impurità nel reticolo metallico.
Il carico a trazione nell’acciaio produce deformazioni elastiche e la sua struttura a corpo cubico centrato può essere distorta sino a diventare a corpo tetragonale centrato. Il carbonio in soluzione solida provoca distorsioni simili a quelle generate da un carico a trazione, ma con una fondamentale differenza: la distorsione media del reticolo causata da un carico trattivo è anisotropica.
Ogni cella del reticolo si allunga nella direzione del carico e, a causa dell’effetto Poisson, si contrae lateralmente.
Gli atomi di carbonio in soluzione solida sono situati nei siti interstiziali del reticolo ed essendo troppo grandi per questi siti generano distorsioni localizzate. Se l’acciaio non è sottoposto a tensioni gli atomi di carbonio si distribuiscono uniformemente nel reticolo generando una deformazione che mediamente è isotropica. L’applicazione di un carico rende invece alcuni siti interstiziali più favorevoli di altri e,durante una prova di trazione, gli atomi di carbonio migrano in questi siti con una dipendenza diretta dal tempo e dalla temperatura: questo può essere causa di una deformazione anelastica. Se si applica istantaneamente un carico di trazione il reticolo metallico subirà una deformazione elastica con una rapidità tale da non permettere alcuna migrazione di atomi ai siti interstiziali più energeticamente favorevoli. Se però il carico viene mantenuto per un certo lasso di tempo la migrazione potrà avere luogo generando un’ulteriore deformazione nel reticolo.
Queste deformazioni, dipendenti dal tempo, sono le deformazioni anelastiche del materiale. Allo stesso modo se il carico viene rapidamente rimosso avremo un ritorno elastico istantaneo mentre il recupero della deformazione anelastica necessiterà di un certo tempo, il tempo necessario agli atomi interstiziali per rientrare nei siti energeticamente più favorevoli. Questa dipendenza dal tempo è mostrata schematicamente :
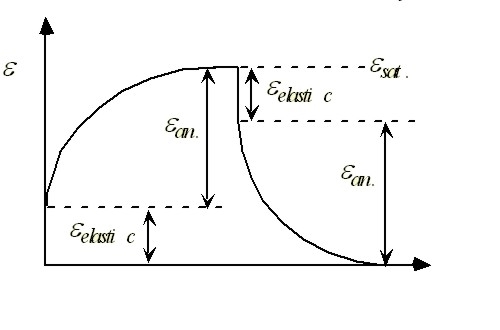
Relazione tra deformazione elastica e anelastica
La combinazione di deformazioni elastica e anelastica può portare ad una dipendenza del modulo di Young dalla rapidità di caricamento e produrre il fenomeno dello smorzamento (descritto in seguito) e frizioni interne nel metallo se questo è soggetto a carichi ciclici o a vibrazioni.
La deformazione anelastica inoltre può causare un rilassamento nella tensione una volta che il carico viene mantenuto ad un dato allungamento. Applicazioni molto lente di un dato carico permettono alla deformazione anelastica di seguire istante per istante il processo di caricamento rendendo la deformazione reversibile totale più grande di quella che si avrebbe per applicazioni più rapide dello sforzo di trazione. Il modulo elastico calcolato per deformazioni lente viene definito “relaxed modulus”, e risulta minore del modulo ricavato da una prova più rapida, modulo chiamato “unrelaxed modulus”.
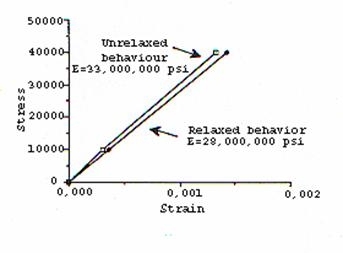
Effetti della rapidità di caricamento sul modulo di Young
Le prove tipiche di trazione si svolgono con rapidità intermedie tra quelle necessarie per ottenere un comportamento rilassato e quelle per averne uno non rilassato. Negli istanti iniziali del test si avrà un comportamento non–rilassato mentre nel periodo successivo, più lungo, avremo un comportamento rilassato. La transizione tra questi due comportamenti produce fenomeni di isteresi di caricamento–scaricamento nella curva tensione – deformazione:
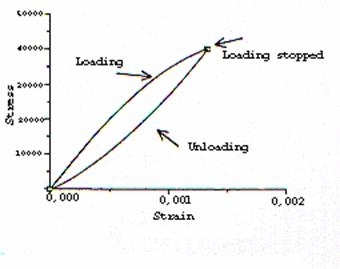
Isteresi nella curva caricamento-scaricamento
Tale fenomeno isteretico rappresenta una perdita di energia nel ciclo caricamento – scaricamento e tale perdita è associata alle frizioni all’interno del reticolo metallico. Questi attriti giocano un ruolo fondamentale nella capacità del materiale di assorbire le vibrazioni. Inoltre generano un aumento di temperatura nel materiale. Una misura della suscettibilità del materiale a questo fenomeno è la sua capacità di smorzamento. I materiali testati in cui si ha una grande produzione di calore a causa dei sopra citati fenomeni isteretici hanno una buona capacità di smorzamento. E’ il caso delle ghise grigie, spesso utilizzate come basamenti per i macchinari poiché permettono di isolare l’ambiente dalle vibrazioni.
Anelasticità , smorzamento e rilassamento della tensione sono fenomeni dipendenti dalla microstruttura del materiale nonché dalle condizioni del test. Essi non vengono misurati tramite la prova di trazione ma ne influenzano i risultati, per cui và tenuto conto della loro presenza.
Nel caso di molti materiali si ha un passaggio graduale dal comportamento elastico a quello plastico e il punto in cui avviene questo passaggio risulta difficile da rilevare. In bibliografia tre sono i criteri adottati per valutare l’inizio dello snervamento.
Limite elastico, che è il massimo valore di tensione che un materiale è in grado di sopportare senza incorrere in deformazioni plastiche irreversibili.
-
Limite di proporzionalità, che è il massimo valore di tensione per cui si abbia ancora proporzionalità tra tensione e deformazione.
-
La tensione di snervamento, che è la tensione necessaria a produrre un ben preciso valore di deformazione plastica (generalmente lo 0,2 %).
Riassumendo, la tensione di snervamento di un metallo può essere definita come la tensione alla quale si ha una sostanziale deviazione dalla proporzionalità tra tensione e deformazione. Piccole deviazioni possono essere dovute a fenomeni di anelasticità che però sono totalmente reversibili e non indicano l’inizio dello snervamento. Valori teorici della tensione di snervamento possono essere calcolati con equazioni del tipo :
s teorica = E / 2 p
Questo genere di relazioni sovrastimano il valore della tensione di snervamento di un fattore pari sino a 100, come si può notare in tabella.
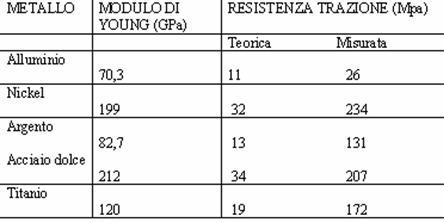
Modulo elastico e resistenza a trazione (teorica e misurata) per alcuni metalli alla temperatura di 20°C
L’instaurarsi di deformazioni permanenti nei cristalli metallici, e quindi l’allontanamento dalle posizioni di equilibrio degli atomi, viene causato da uno scorrimento dei piani atomici gli uni rispetto agli altri con rottura dei legami. L’energia richiesta per attivare questo meccanismo risulta molto minore in presenza delle dislocazioni e sono proprio le dislocazioni la causa della discrepanza tra la tensione teorica e quella effettiva. La figura illustra i due meccanismi di deformazione plastica:
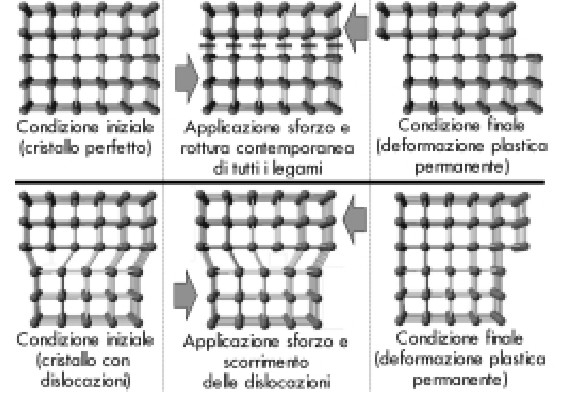
Deformazione plastica prodotta per spostamento in blocco tra piani reticolari e per scorrimento di dislocazione
Le dislocazioni sono fisicamente dei difetti di linea del reticolo cristallino. Il loro movimento e la loro interazione con altri difetti reticolari sono alla base del fenomeno della deformazione plastica nei metalli. Vi sono tre categorie di difetti del reticolo metallico :
-
Difetti di punto, cioè deviazioni su una scala di due o tre distanze atomiche. Si parla allora di vacanze o lacune in cui si hanno posizioni reticolari non occupate, difetti interstiziali o costituzionali.
-
Difetti di linea o dislocazioni.
-
Difetti di superficie come i bordi di grano e seconde fasi.
L’interazione tra questi difetti modifica il comportamento meccanico del materiale durante lo snervamento alterando il moto delle dislocazioni.
Il moto delle dislocazioni dipende dagli elementi leganti, dalle lavorazioni a freddo, dalla distribuzione e dimensione delle inclusioni nel reticolo e dalle dimensioni dei grani. La resistenza di molti metalli viene accresciuta con l’aumentare degli elementi di lega che, interagendo con le dislocazioni, ne inibiscono la mobilità. La lavorazione a freddo è un altro metodo per rafforzare un materiale. Con questa tecnica si ha un aumento nel numero delle dislocazioni che ad un certo punto si ostacolano tra di loro. Anche un affinamento dei grani, aumentando i bordi di grano, incrementa la densità di difetti nel reticolo. In questo modo il moto delle dislocazioni risulta ostacolato.
Alcuni metalli ed in particolar modo gli acciai a basso tenore di carbonio, presentano una transizione eterogenea tra deformazione elastica e plastica che produce un punto di snervamento nella curva tensione – deformazione:
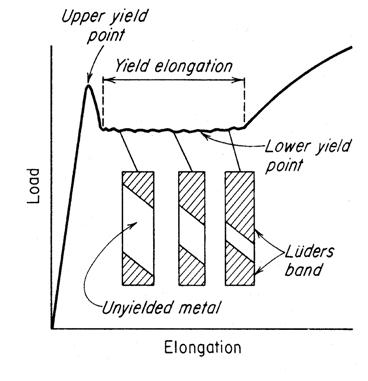
Tipico comportamento a trazione di un acciaio a basso tenore di carbonio
L’inizio del moto delle dislocazioni non sarà più un processo graduale ma avverrà in un breve lasso di tempo. Il carico crescerà con la deformazione raggiungendo un massimo,il cosiddetto punto di snervamento superiore (upper yield point), per poi decadere, fluttuare attorno ad un valore approssimativamente costante, detto punto di snervamento inferiore (lower yield point) e poi riprendere ad aumentare con un’ulteriore deformazione. L’allungamento che si ha a carico costante , il lower yield point, è chiamato yield point elongation (YPE).
L’ yield point si sviluppa a causa di un’interazione tra le dislocazioni e le atmosfere di soluto nel reticolo. Una linea di dislocazione rappresenta di fatto una regione deformata del reticolo ed è accompagnata da un campo di tensioni elastiche, con zone in compressione e in trazione. Questo produce fenomeni di natura chimica come la segregazione degli atomi di soluto attraverso il reticolo nelle zone deformate. Si vengono così a creare delle atmosfere di soluto da cui la dislocazione deve separasi per procedere nel proprio movimento. Quando questa separazione ha luogo la tensione necessaria a far procedere la deformazione decresce raggiungendo il lower yield point.
Questo processo di snervamento è un fenomeno locale di deformazione plastica e le regioni in cui si sviluppa sono dette bande di Luders. Tipicamente tali bande si vengono a formare in punti di concentrazione delle tensioni (imperfezioni nel reticolo metallico) e si sviluppano generalmente con un angolo di 45° rispetto all’asse del provino. L’andamento irregolare della curva durante l’yield point elongation nasce da una continua formazione di bande di Luders. L’angolo di 45° deriva dal fatto che le dislocazioni si muovono preferenzialmente lungo piani di massima densità atomica, disposizioni bidimensionali del reticolo dove gli atomi sono più strettamente disposti e che nei metalli si hanno proprio per angoli di 45°. Essendo la densità atomica generalmente costante nei metalli i piani più densi dovranno essere tra loro maggiormente spaziati. Pertanto le corrispondenti forze interplanari saranno più deboli con l’effetto di rendere i piani di massima densità quelli a più facile scorrimento.
Un aumento della deformazione provoca il propagarsi delle bande di Luders sino a che tutta la sezione di prova ne viene interessata. A questo punto la tensione riprende a crescere a causa dell’ interazione delle dislocazioni che, ostacolandosi, portano al fenomeno dell’ incrudimento.
I metalli e le leghe tipicamente usate in ingegneria sono materiali policristallini. Un tipico oggetto metallico contiene decine di migliaia di cristalli microscopici detti grani.
Assumendo per semplicità il grano come una sfera di diametro d esiste una relazione tra questo e la tensione di snervamento ss di un materiale, l’equazione di Hall – Petch :
ss = s0 + Kd-0,5
Dove:
s0 è la resistenza offerta al moto delle dislocazioni da parte del cristallo
k è una costante empirica che dipende dal materiale e dai bordi di grano.
Graficamente gli effetti dei bordi di grano:
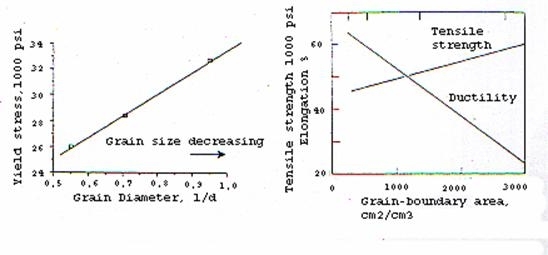
Effetti della dimensione dei grani sulla resistenza e duttilità dei metalli
I bordi di grano agiscono come delle barriere al moto delle dislocazioni. Una dislocazione può non essere in grado di superare l’ostacolo ed allora si verifica un accumulo di dislocazioni.
Il superamento della barriera da parte delle dislocazioni accumulate esercita un’azione meccanica collettiva sul bordo di grano, una cosiddetta dislocazione gigante, che corrisponde macroscopicamente allo snervamento.
Il numero di dislocazioni che si possono accumulare dipende essenzialmente dalle dimensioni del grano. Se il grano è di grandi dimensioni avremo un elevato numero di dislocazioni che si accumulano con conseguente marcato snervamento una volta superata la barriera. In materiali a grana più fine invece avremo un ostacolo alle dislocazioni più uniformemente distribuito: questo porterà ad avere un limite elastico più grande e quindi una tensione di snervamento più alta.
La curva tensione-deformazione nominale non dà indicazioni reali sul comportamento di un materiale. Essa si basa infatti sulle dimensioni originali del provino, dimensioni che in realtà variano continuamente durante il test. Il carico decresce una volta raggiunto il suo massimo a causa di una diminuzione sostanziale della sezione resistente,ed essendo la tensione proporzionale al carico, essa decresce ugualmente.
Nella curva reale invece si tiene conto della diminuzione di tale sezione nel calcolo della tensione: ne risulta una curva che cresce continuamente sino alla frattura:
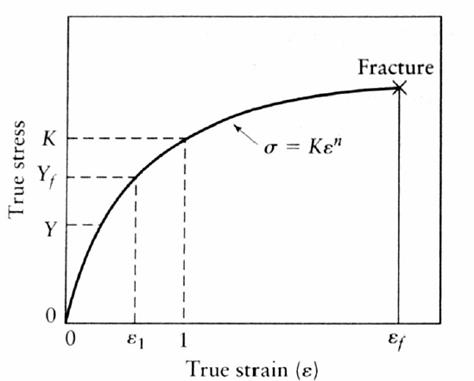
Curva tensione-deformazione effettiva
La curva tensione-deformazione reale è anche chiamata curva di flusso poiché rappresenta,punto per punto, il flusso plastico caratteristico di un dato materiale.
La tensione effettiva s:
s = F / A
Dove A è l’area della sezione nell’istante in cui è applicato il carico F.
La deformazione reale e:
e = Ln (L / L 0)
Quest’ultima definizione viene ottenuta considerando un incremento infinitesimo della deformazione ad un dato istante ed integrandolo.
Fintanto che la deformazione è uniforme è possibile legare i valori reali di tensione e deformazione effettivi a quelli nominali. Sfruttando la costanza di volume del provino:
L A0 = LA
Si ottiene allora :
s = s (1 + e) (x)
e = Ln (1 + e) (y)
Da notare che per tensioni relativamente basse i valori nominali ed effettivi praticamente coincidono.
Le equazioni x e y sono valide anche dopo la strizione a patto che nella prima l’area venga calcolata direttamente e non basandosi sulle misure di lunghezza e che nella seconda si faccia riferimento al diametro attuale D:
e = 2 Ln (D0 / D)
Tipicamente la curva di flusso risulta lineare a partire dal carico massimo sino alla rottura. In altri casi invece essa decresce. La strizione, una volta raggiunto il carico massimo, introduce uno stato tensionale tridimensionale decisamente più complesso di quello uniassiale di trazione e questo rende difficile la valutazione della tensione a partire dalla strizione sino alla rottura.
La curva di flusso nella regione di deformazione plastica può essere espressa dalla relazione di Holloman:
![]()
Dove n è il cosiddetto esponente di incrudimento e K è un coefficiente di resistenza. Come si può vedere, riportando l’equazione in un diagramma in scala logaritmica si perviene ad una retta la cui pendenza è proprio n. K rappresenta la tensione in corrispondenza di una deformazione unitaria.
Il valore di n varia tra 0, relativamente a solidi perfettamente plastici, e 1, per solidi elastici. Tipicamente per gli acciai n varia tra 0,1 e 0,50.
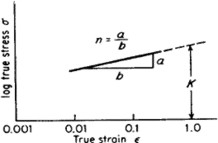
Curva tensione-deformazione effettiva logaritmica
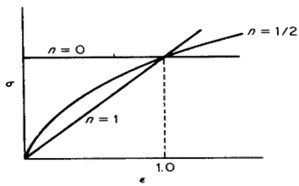
Varie forme della curva di Holloman
È possibile anche ricavare la rapidità con cui un materiale incrudisce. Essa non coincide con l’esponente n e si può calcolare dalla definizione di esponente di incrudimento:
![]()
da cui la rapidità di incrudimento:
![]()
Deviazioni dall’equazione della curva di flusso si possono avere per piccole o grandi deformazioni. Sono state proposte altre correlazioni, come ad esempio l’equazione di Ludwik, una generalizzazione della relazione di Holloman :
![]()
Dove s0
è la tensione di snervamento. Tale relazione ha validità più generale della precedente, che sottintendeva una tensione pari a zero in caso di deformazione nulla.
Confronto tra le due rappresentazioni, effettiva e nominale:
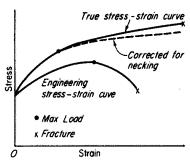
Confronto tra curve tensione-deformazione reale ed effettiva
Si nota come il massimo della curva nominale si abbia a causa dell’instabilità della tensione e non per un calo nella resistenza del materiale. La diminuzione della tensione nel diagramma nominale è artificiosa poiché si basa sull’area di sezione iniziale del provino.
L’instabilità nella tensione, come si vedrà in seguito, coincide con l’inizio della strizione nel provino. Tale fenomeno nasce da una localizzazione della deformazione plastica e quindi, una volta che ha preso piede, la deformazione reale non è più calcolabile a partire dall’allungamento del provino.
Da tutte queste osservazioni si intuisce come, se i dati del test a trazione vengono usati per comprendere e prevedere il comportamento metallurgico durante una deformazione associata ad una lavorazione , le relazioni di tensione e deformazione effettive sono da preferire a quelle nominali.
Il nichel all’ 1% di deformazione la tensione di scorrimento,cioè la tensione necessaria a perpetrare una deformazione, è di 330 Mpa , mentre al 10 % sale a 415. Questo aumento nella tensione è dovuto al meccanismo dell’incrudimento.
A snervamento sopravvenuto la deformazione plastica procede per moto delle dislocazioni lungo il provino. Una dislocazione, fintanto che non intervengano sforzi esterni, si mantiene rettilinea per minimizzare la propria energia totale. Quando uno sforzo esterno mobilizza la dislocazione la sua linea si incurva sino a quando la dislocazione originaria non si sdoppia: una si espande sotto lo sforzo applicato e l’altra cerca di ripristinare la sua natura rettilinea di minimo energetico.
In tal modo si viene a creare una vera e propria sorgente di dislocazioni, dislocazioni che vengono prodotte con il progredire della deformazione. Queste sorgenti aumentano enormemente il numero di dislocazioni presenti e che, interagendo tra di loro, si ostacolano a vicenda. Tale meccanismo, definito come incrudimento o strain hardening, aumenta la sollecitazione necessaria ad attivare nuovi sistemi di scorrimento ed è operante sino alla rottura del provino.
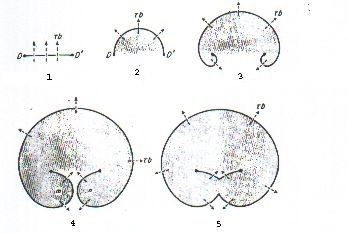
Meccanismo di moto delle dislocazioni proposto da Frank-Read
L’aumento della tensione di scorrimento dovuto all’incrudimento è alla base del rafforzamento operato sui materiali metallici dalla lavorazione a freddo.
Oltre alla resistenza anche la duttilità risente di questa lavorazione: essa decresce con l’aumento della lavorazione a freddo, tanto che ad un certo livello di lavorazione si può avere eccessivo infragilimento e conseguente rottura del materiale.
Da notare che un aumento nella resistenza e un calo nella duttilità porta ad una diminuzione dell’area sottostante il diagramma tensione–deformazione. Questo è significativo in quanto tale area rappresenta l’energia necessaria a portare a rottura il materiale. La deformazione ottenibile senza frattura, ad esempio in un’operazione di imbutitura, varia di materiale in materiale.
Ad esempio gli acciai austenitici possono essere imbutiti con successo sino ad una riduzione di sezione del 50 % mentre per quelli ferritici si arriva al massimo al 30 %. Questa differenza può essere correlata con l’esponente di incrudimento n. Tale coefficiente è associato alla capacità delle dislocazioni di superare ostacoli come bordi di grano o inclusioni.
Quando ciò avviene senza difficoltà le dislocazioni non si accumulano e l’esponente n risulta basso. Acciai dolci, l’alluminio e alcune leghe del nichel sono esempi di materiali che non incrudiscono.
Il valore di n cresce invece se le dislocazioni trovano difficoltà nel superare delle barriere e questo accade ad esempio negli acciai austenitici o per le leghe del rame.
L’incrudimento provoca un innalzamento della tensione di scorrimento aumentando di conseguenza il carico necessario per continuare a deformare plasticamente il provino. Ne segue che la deformazione è costretta a svilupparsi su tutta la sezione di prova. Più alto è il valore di n più alta è la tendenza della deformazione plastica a diventare uniforme e questo ha un notevole impatto sulla lavorabilità di un materiale.
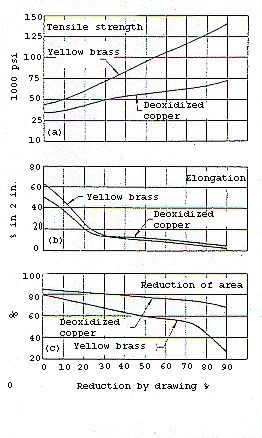
Effetti della lavorazione a freddo sulle proprietà meccaniche del rame e dell'ottone. (a) Resistenza a trazione, (b) Elongazione, (c) Riduzione d'area.
La capacità di un materiale di incrudirsi è tipica dei metalli e delle leghe.
I materiali fragili non presentano snervamento e si fratturano senza traccia di incrudimento.
Generalmente invece, i metalli presentano evidenti deformazioni plastiche prima di arrivare a rottura e la tensione a cui essa avviene e apprezzabilmente più grande della tensione di snervamento. Tale tensione è la resistenza del materiale alla trazione. Il margine tra snervamento e rottura fornisce una fattore di sicurezza in condizioni di funzionamento ma malgrado questo la resistenza a trazione è un parametro usato raramente in progettazione.
La strizione in un test di trazione generalmente inizia al massimo carico.
Il provino si trova sottoposto a due fenomeni contrastanti: da un lato il materiale incrudisce aumentando la capacità di sostenere il carico, dall’altro la sezione resistente diminuisce dando un effetto opposto al fenomeno precedente.L’instabilità che conduce alla deformazione localizzata viene descritta tramite la condizione dP=0,ove P è il carico applicato:
![]()
Dalla costanza del volume:
![]()
Infine, dalla condizione di instabilità, si perviene a :

Risulta quindi che nella curve tensione-deformazione effettiva il punto in cui si ha strizione al massimo carico può essere ottenuto trovando il punto della curva con una sottotangente unitaria.
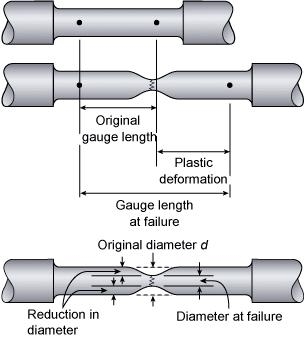
Meccanismo della strizione (necking)
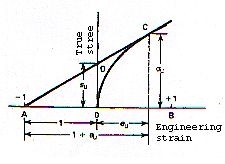
Costruzione di Considerè per determinare il punto di massimo carico
La formazione di una strizione in un provino soggetto a trazione produce un complesso stato triassiale di tensione. La rastremazione genera una tensione radiale ed una circonferenziale che determinano un aumento nella tensione necessaria ad avere scorrimento plastico.
Una correzione dello sforzo assiale a causa dell’introduzione di tensioni circonferenziale è stata proposta da Bridgman. Tale analisi si basa sulle seguenti ipotesi semplificative:
-
Il contorno della strizione è approssimabile ad un arco di cerchio.
-
La sezione del provino rimane circolare durante il test.
-
Le deformazioni rimangono uniformi nella sezione trasversale della strizione.
La relazione di Bridgman:
s = (s) AVG / ( ( (1 + 2R) / a ) . ( ln ( 1 + a / 2 R ) ) )
Dove (s) AVG è la tensione media ottenuta dividendo il carico per la sezione strizionata, a è il raggio minimo alla strizione ed R è il raggio di curvatura della zona strizionata.
La duttilità è la capacità di un materiale di deformarsi plasticamente senza rompersi.
Per valutarla due sono le misure più comunemente adottate in una prova a trazione: l’allungamento percentuale e la riduzione percentuale dell’area di sezione del provino,rispettivamente:
% E I = ( ( Lf - L0 ) / L 0 ) x 100
% R A = ( ( A0 - Af ) / A0 ) x 100
Dove L f e A f sono la lunghezza e l’area di sezione finali del provino. Se la rottura avviene senza strizione esiste una relazione tra questi due valori :
% E I = ( % R A ) / (100 - % R A)
La duttilità di un metallo dipende fortemente dalla geometria del provino e dai trattamenti meccanici come la lavorazione a freddo, ma anche, come si vedrà, dalla rapidità con cui viene condotta la prova e dalla temperatura.
La capacità di assorbire energia senza rompersi viene definita come la tenacità di un materiale.
La quasi totalità delle fratture ha inizio da imperfezioni preesistenti nel materiale, come cricche o fessure. Un materiale tenace è in grado di resistere alla propagazione della cricca attraverso lo snervamento e la deformazione plastica.
Per stimare la tenacità è possibile utilizzare la curva tensione–deformazione, infatti l’area sotto la curva è una misura dell’energia assorbita dal materiale durante il test a trazione. Essendo la deformazione plastica di diversi ordini di grandezza più grande di quella elastica appare evidente quanto il meccanismo della plasticizzazione e il moto delle dislocazioni siano fondamentali nello sviluppo della tenacità. La rottura fragile ha luogo con deformazioni plastiche trascurabili e dunque detta A l’area sotto la curva tensione–deformazione risulta :
A = 1/2 s e
Essendo poi la deformazione quasi completamente elastica vale la legge di Hooke s = E e
avremo :
A = 1/2 sf2 E
Dove sf
è la tensione di rottura. Se invece il provino è duttile l’area sotto la curva può essere così stimata :
A = ( ss + sf ) . ( er / 2)
dove er è la deformazione a frattura.
Incrementare la resistenza di un metallo in genere riduce la duttilità compromettendo di conseguenza la tenacità.
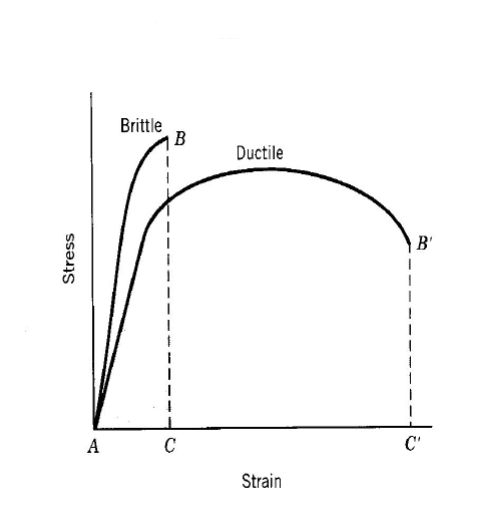
Esempi di comportamento fragile e duttile
La capacità di un metallo di assorbire energia durante la deformazione elastica è definita come resilienza. Il modulo di resilienza viene rappresentato dall’area sotto la curva tensione-deformazione nella regione elastica. Tale area risulta :
A = 1 / ( 2 E ) ss2
Incrementare la tensione di snervamento e/o decrescere il modulo E aumenta la capacità del materiale di assorbire energia senza incorrere in deformazioni permanenti.
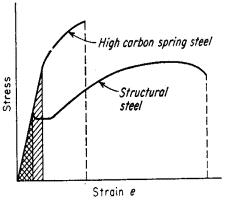
Curve tensione-deformazione per materiali a diversa tenacità. Le zone ombreggiate rappresentano il modulo di resilienza dei due materiali.
Se il test di trazione viene condotto su di un provino ricavato da una lastra metallica risulta molto importante l’orientazione con cui è sottoposto a trazione. Le lavorazioni a freddo quali rullatura, imbutitura e stampaggio modificano la forma dei grani cristallini e tale forma dipende essenzialmente dalla direzione di scorrimento durante la lavorazione.
Oltre a questo si verifica una sostanziale distorsione dei grani con creazione di bande ad alta densità di dislocazioni. Le deformazioni del reticolo cristallino risultano sostanzialmente anisotropiche come anisotropiche saranno le proprietà del materiale lavorato. Un parametro molto utilizzato per valutare l’anisotropia di un lastra di metallo è il rapporto di deformazione plastica r ,definito come il rapporto delle deformazioni di contrazione misurate in un provino posto a trazione:
![]()
Dove ew è la deformazione in larghezza e et è quella lungo lo spessore. Il valore di r risulta unitario in caso di materiale isotropico.
Per provini di spessore molto ridotto una misura di una sua variazione può risultare difficile. Ci si basa allora sulla conservazione del volume:
![]()
Dove el è la deformazione lungo l’asse di caricamento del provino. Sostituendo otteniamo:
![]()
Per evitare l’influenza da parte delle estremità del provino serrate sulla macchina,le deformazioni devono essere misurate ad una certa distanza rispetto alle spalle del campione, pari ad almeno la sua larghezza.
Il valore di r dipende molto dalla direzione in cui viene tagliata la lamiera. In tal caso si tiene conto di un valore medio di r:
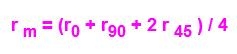
I pedici si riferiscono all’angolo tra l’asse di trazione nella prova e la direzione di rullatura.
Il grado di anisotropia nel piano della lastra viene descritto dal parametro.
![]()
Nella maggior parte dei metalli la resistenza allo snervamento tende a crescere con la rapidità di deformazione e a diminuire con l’ innalzamento della temperatura. Questa dipendenza dalla rapidità deformativa e dalla temperatura, viene influenzata da numerose variabili metallurgiche.
Ad esempio le dislocazioni sono a tutti gli effetti degli spostamenti ed in quanto tali non possono muoversi più velocemente della velocità del suono. Se la rapidità della dislocazione si avvicina a questo valore avremo un aumento nell’esponente di incrudimento n dato dal fatto che diviene molto difficile per le dislocazioni superare delle eventuali barriere come ad esempio i bordi di grano e a tale aumento corrisponde un incremento nella resistenza allo snervamento.
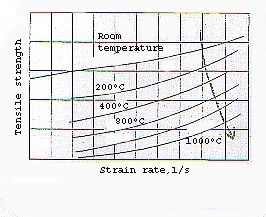
Effetti della temperatura e della strain rate sulla resistenza dell'ottone
Un altro possibile effetto è quello di riduzione della duttilità con una transizione dal comportamento duttile ad un comportamento fragile. Per molti aspetti un abbassamento di temperatura è simile ad un aumento della rapidità deformativa: la mobilità delle dislocazioni diminuisce e si ha un incremento nella resistenza a snervamento ed una diminuzione di duttilità.
Il movimento delle dislocazioni può essere inibito dall’interazione con altre dislocazioni o con atomi interstiziali e gli effetti di queste interazioni sono dipendenti dal tempo e dalla temperatura. La dipendenza dalla temperatura è ovvia, in quanto una sua variazione modifica la mobilità degli atomi nel reticolo metallico.
Per quanto riguarda la dipendenza temporale tali processi risultano più efficaci quando vi è sufficientemente tempo per gli atomi di segregare dalla dislocazione e quando la velocità della dislocazione è approssimativamente uguale alla rapidità di diffusione degli atomi di soluto. Perciò ad una data temperatura gli effetti delle interazioni tra dislocazioni e atomi in soluzione avranno un loro massimo ad una data rapidità di deformazione. A basse velocità la diffusione può avvenire alla stessa velocità del moto della dislocazione e non vi è alcuna tendenza al distacco tra dislocazione e relativa atmosfera di soluto. Ad alte velocità invece, una volta che si è operato il distacco, non c’è il tempo materiale di ristabilire tali atmosfere e questo porta all’ incrudimento.
Gli effetti tempo–dipendenti delle interazioni tra difetti di linea e difetti di punto nei metalli sono definiti come invecchiamento per deformazione (o strain aging) e invecchiamento dinamico per deformazione. Questi fenomeni sono evidenti quando si interrompe la prova trazione di un materiale che esibisce un’ upper yield point. Supponiamo che il provino venga tensionato attraverso lo snervamento, la formazione delle bande di Luders e l’incrudimento e che poi venga scaricato. Se successivamente il carico viene riapplicato entro un breve intervallo di tempo la porzione elastica della curva del nuovo caricamento risulterà parallela alla prima e la deformazione plastica avverrà allo stesso livello di tensione del primo caricamento ma senza la presenza dell’ upper yield point. Se invece l’intervallo di tempo tra le due prove è sufficientemente lungo da permettere una segregazione da parte degli atomi di soluto il punto di snervamento riapparirà ad una tensione superiore rispetto al primo test con una ricomparsa dell’upper yield point.
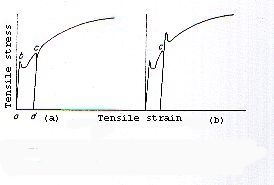
Invecchiamento per deformazione in una prova di trazione a interruzione. (a) carico riapplicato dopo un breve periodo, (b) carico riapplicato dopo un tempo sufficiente
Se poi le velocità di deformazione permettono la segregazione degli atomi di soluto si può osservare il cosiddetto invecchiamento dinamico. La segregazione del soluto blocca le dislocazioni precedenti e incrementa la tensione di scorrimento. Quando la nuova tensione massima di scorrimento viene raggiunta le dislocazioni sono libere dalle atmosfere di soluto e la tensione diminuisce. Questa alternanza tra aumento e diminuzione delle tensioni di scorrimento genera una curva tensione – deformazione di forma seghettata, comunemente osservabile negli acciai dolci e nelle leghe di alluminio.
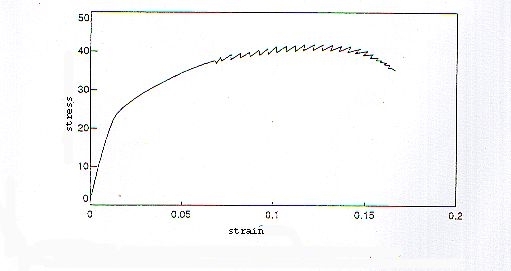
Invecchiamento dinamico per deformazione in una lega di alluminio a temperatura ambiente
La prova di trazione può produrre due tipi di rottura del provino: duttile e fragile.
Le fratture duttili sono caratterizzate dalla lacerazione del metallo e da un notevole dispendio di energia per essere prodotte. Generalmente si presentano con un aspetto fibroso e vengono classificate in scala macroscopica come fratture piane, cioè ortogonali all’asse di caricamento del provino, oppure di taglio se la rottura avviene lungo un piano inclinato di 45° rispetto a tale asse.
Le rottura fragili sono caratterizzate da una rapida propagazione della frattura, con assenza di sostanziali deformazioni plastiche ed un energia spesa per arrivare a rottura considerevolmente inferiore a quella dei materiali duttili. La sezione di rottura presenta un aspetto ben definito, lucente e granuloso, mentre la strizione praticamente non è presente.

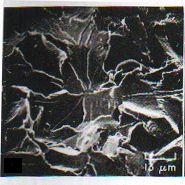
Esempi di superfici di rottura duttile (a) e fragile (b).
Quando in un materiale soggetto a tensione è presente una cricca, la tensione locale nel suo intorno è maggiore di quella applicata all’intero provino. Si dice che la cricca ha l’effetto di concentrare lo sforzo. Un’analisi matematica mostra che la tensione locale per una cricca aguzza in un materiale elastico è :
![]()
Dove s
la tensione del provino, a è una costante dipendente dal materiale e r è il raggio della cricca. Avvicinandosi all’apice della cricca la tensione locale diventa più elevata sino a superare la tensione di snervamento del materiale e si ha quindi lo sviluppo di una deformazione plastica.
La propagazione della cricca e l’area interessata dalla deformazione dipendono strettamente dalla tensione di snervamento: al suo aumentare la zona plastica si riduce rapidamente, tanto che nei materiali fragili praticamente non è presente.
Sequenza di eventi che porta alla frattura coppa – cono, tipico esempio di rottura duttile. La propagazione delle cricche ha inizio nel centro della strizione. Esse si vengono a formare in seguito a fenomeni di decoesione dei grani cristallini o per spaccature nei grani delle seconde fasi. Si può osservare in seguito una coalescenza delle cricche che porta ad una macroscopica fenditura che si propaga poi sino alla superficie del provino producendo la rottura definitiva.

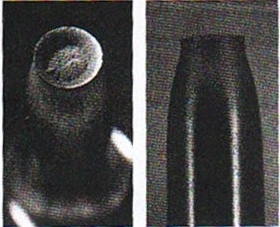
Frattura coppa-cono
Sviluppo della rottura coppa-cono in un provino a trazione (a) e immagine della stessa (b)
L’analisi della propagazione della cricca è analoga alla precedente, solo che questo meccanismo, comunemente chiamato clivaggio, si realizza in materiali ad elevata tensione di snervamento e quindi caratterizzati da piccole zone di deformazione plastica. Ciò porta ad avere cricche aguzze con elevate intensificazioni degli sforzi all’apice della cricca. La cricca si propaga per rottura dei legami atomici e quasi assenza di componenti dislocative.
Ne risulta una superficie di frattura netta e caratterizzata da un basso assorbimento di energia nella sua formazione,caratterizzata da increspature radiali che partono dal centro del provino propagandosi sino alla superficie esterna. Esse sono parallele alla direzione di propagazione della rottura e vengono prodotte quando due spaccatura non complanari si uniscono con conseguente lacerazione del materiale intermedio.
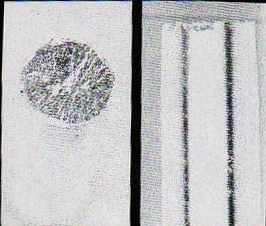
Esempio di rottura fragile
Portale "Ingegneria e
Campanologia" -
Autore -
Sommario
- Mappa del Sito -
Home
Bib-TS-147 - Michele Cuzzoni, Appunti di Scienza delle Costruzioni - Università degli Studi di Pavia - Facoltà di Ingegneria - AA. 1995 - 1996
Bib-TS-148 - Michele Cuzzoni, Appunti di Tecnica delle Costruzioni - Università degli Studi di Pavia - Facoltà di Ingegneria - AA. 1996 - 1997.
Bib-TS-153 - Michele Cuzzoni, Appunti di Meccanica dei Solidi - Università degli Studi di Pavia - Facoltà di Ingegneria - AA. 1995 - 1996
Bib-TS-154 - R. Baldacci, Scienza delle Costruzioni, Vol. I e II, UTET, 1993
Bib-TS-155 - Michele Cuzzoni, Applicazioni pratiche per campana: rielaborazione di studio realizzato nel 1997. Disegno, rifacimento 2008