Portale "Ingegneria e Campanologia" - Autore - Sommario - Mappa del Sito - Home
Meccanica del mezzo continuo e dei
materiali
AREA I - ARTE TECNICO-SCIENTIFICA (ATS)
Cap. ATS-H01 - Meccanica - Pag. ATS-H01.12
Gli argomenti trattati sono stati inseriti da Ing. Arch. Michele Cuzzoni nel 2012 - © Copyright 2007- 2024 - e sono desunti dalla documentazione indicata in Bibliografia a fondo pagina
- Prove meccaniche dei materiali
- Nozione storica
- Proprietà meccaniche - influenza della temperatura
- LA PROVA DI TRAZIONE
- Andamento tipico della curva di trazione
- Prova di trazione UNI EN 10002 - fa riferimento alla normativa 1
- Redistribuzione delle sollecitazioni in presenza di una cricca
- PROVA DI TRAZIONE SU PROVETTA CON INTAGLIO
- La prova del pendolo di Charpy
- Tenacità alla frattura
- FATICA
- APPLICAZIONE DEI DATI DI MECCANICA DELLA FRATTURA
Codice di Hammurabi (2250 a.C.): "...Se un costruttore edifica una casa per un uomo senza che questa sia stabile, e la casa che ha costruito crolla e causa la morte del proprietario della casa, che il costruttore sia messo a morte. Se il crollo causa la morte di un figlio del proprietario, che sia messo a morte un figlio del costruttore. Se distrugge una proprietà, dovrà ricostruirla e, dato che non ha costruito la casa in maniera stabile, la ricostruirà a proprie spese..."
Prenderemo in esame le caratteristiche meccaniche dei materiali metallici, intendendo con questo termine quei dati, ottenuti attraverso prove unificate, che servono a stabilire se un materiale è adatto all'impiego previsto.
I metodi di prova sono concettualmente identici a quelli adottati a temperatura ambiente, con la complicazione di doverli applicare in condizioni criogeniche. I risultati sono variamente influenzati dalla temperatura in relazione alla struttura cristallina, alla composizione chimica ed al tipo di sollecitazione.
E' la più importante prova convenzionale meccanica. Si esegue su ogni materiale allo scopo di rilevare le caratteristiche di resistenza, deformabilità e di elasticità: è fondamentalmente una prova di collaudo, di riconoscimento, di selezione.
Con la prova di trazione statica si ricavano indici di confronto che consentono la formulazione di giudizi relativi allo stato del materiale ed alle possibilità del suo impiego. Questa prova costituisce il mezzo di controllo dei processi tecnologici (stampaggio, fucinatura, saldatura, trattamenti termici, ecc.) offrendo al progettista valori di riferimento per il calcolo e il dimensionamento degli organi di macchine.
La prova di trazione consiste nel sottoporre un provino, le cui dimensioni devono rispondere a certe prescrizioni, ad una forza di trazione lungo il suo asse, con una velocità di deformazione controllata, sino alla rottura.
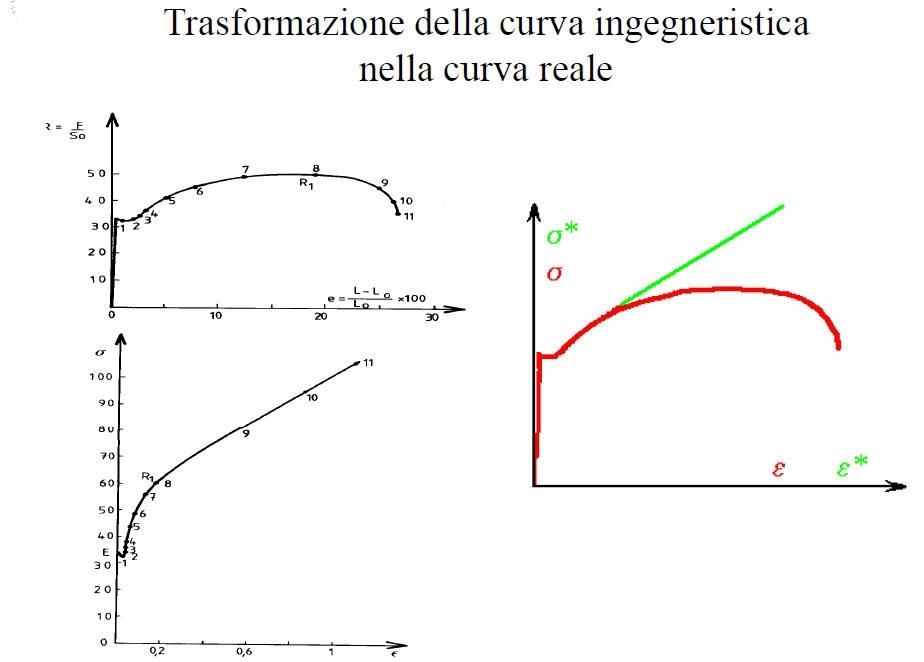
Si rileva il diagramma tensione-deformazione, intendendo con tensione il rapporto tra il carico applicato e la sezione iniziale, e con deformazione il rapporto tra l'allungamento di un tratto di riferimento e la sua lunghezza iniziale.
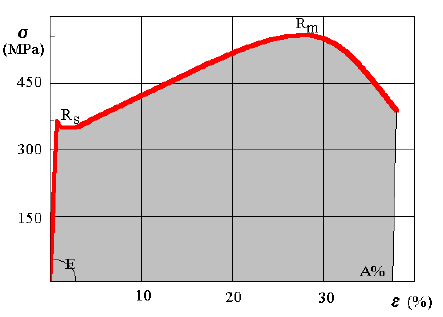
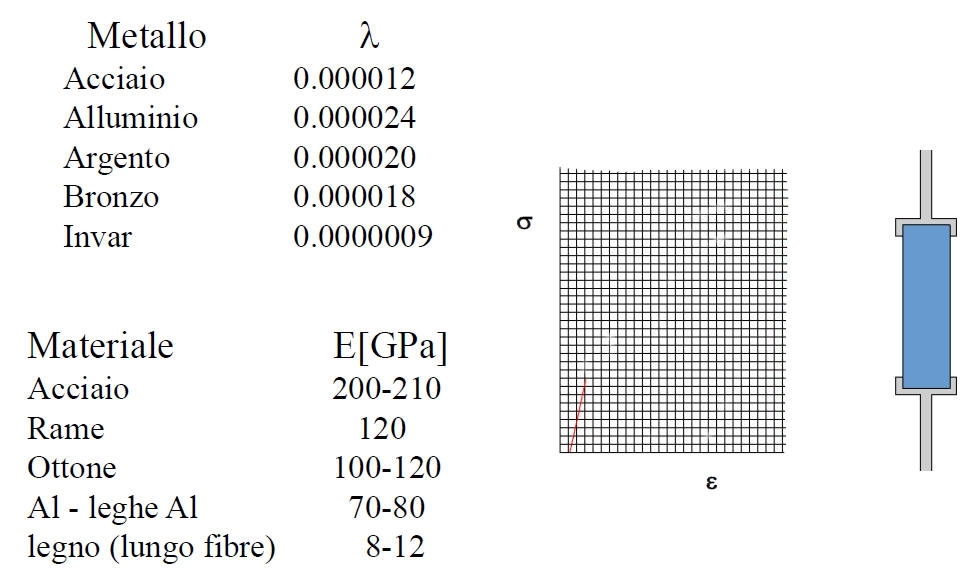
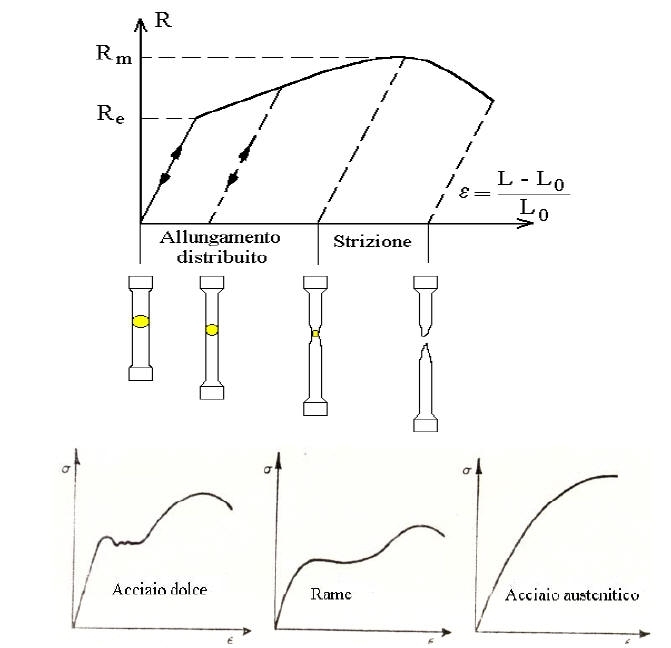
Il diagramma, che ha indicativamente la forma rappresentata in figg. 0 e 1, presenta un primo tratto iniziale rettilineo, nel quale la tensione è proporzionale alla deformazione, essendo il coefficiente di proporzionalità il modulo di Young, E, del materiale.
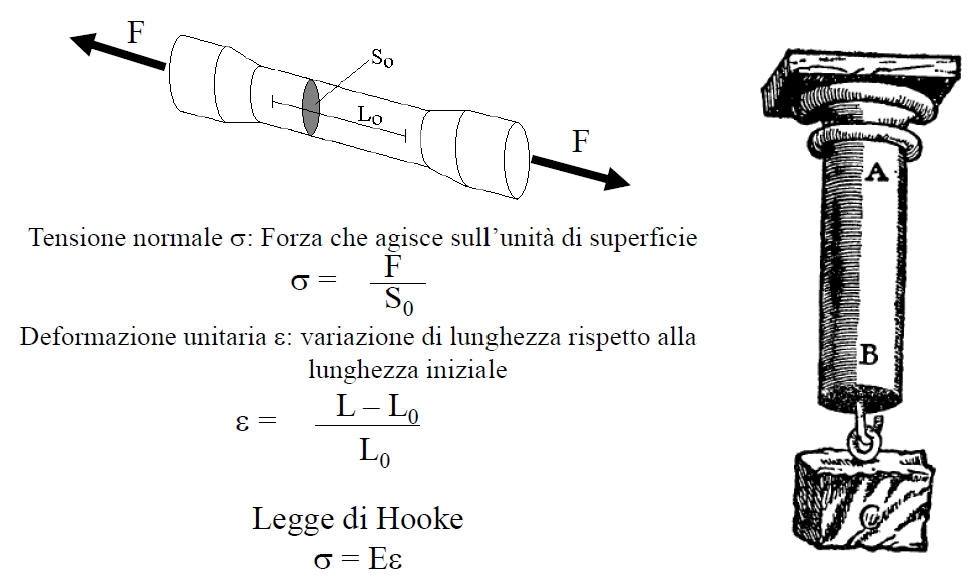
Fig.0 - Prova di trazione
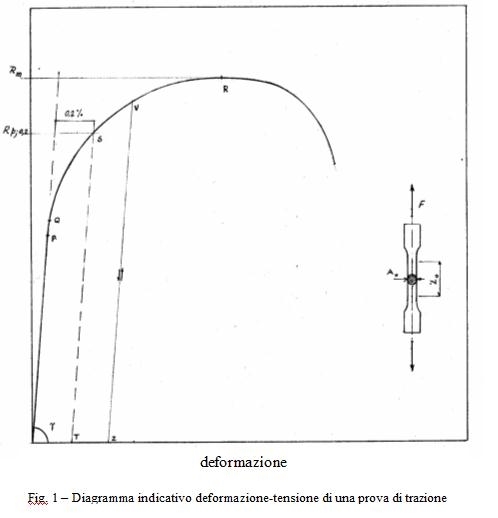
In questa fase se il provino viene scaricato riprende la sua lunghezza iniziale. Il comportamento è elastico.
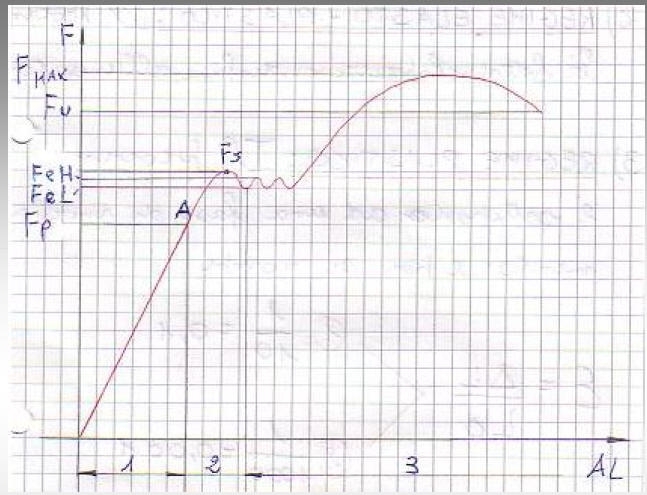
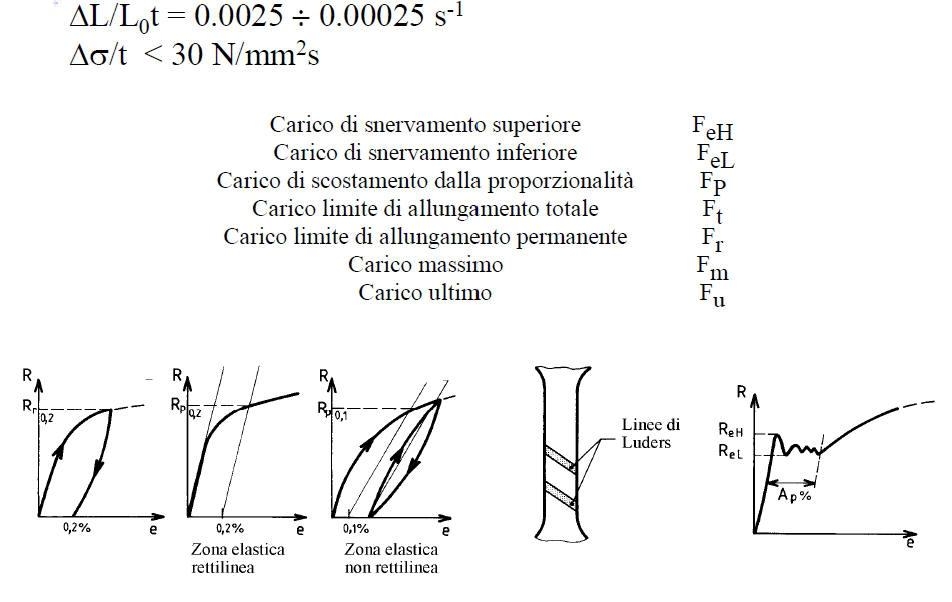
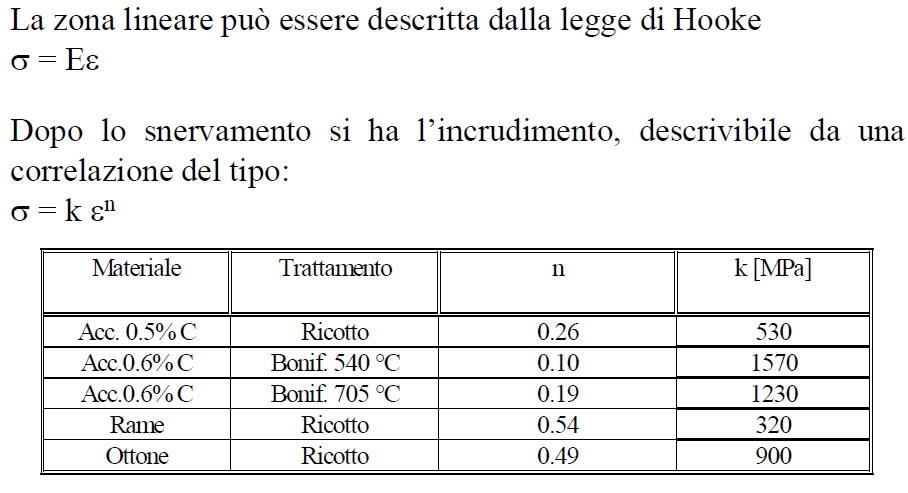
Proseguendo nella deformazione il diagramma abbandona l'andamento rettilineo, la deformazione si compone ora di una parte plastica, che non scompare eliminando la tensione, e che corrisponde circa allo scostamento della curva dalle legge di proporzionalità. Si assume come parametro di questa transizione la tensione che produce uno scostamento dalla proporzionalità dello 0,2%: Rp;0,2. La deformazione plastica avviene a volume costante.
Proseguendo la forza cresce sempre meno, sino ad un massimo (se non interviene prima la rottura). Il fenomeno per il quale la forza necessaria a produrre la deformazione plastica cresce con la deformazione stessa è detto incrudimento.
La tensione corrispondente al massimo è la resistenza a trazione del materiale, Rm.
La deformazione, sino a questo punto è stata uniforme nel tratto a sezione costante di riferimento. A partire dal massimo compare in una sezione del provino un restringimento, strizione, dove si concentra l'ulteriore deformazione e la cui sezione continua a diminuire, sino a rottura.
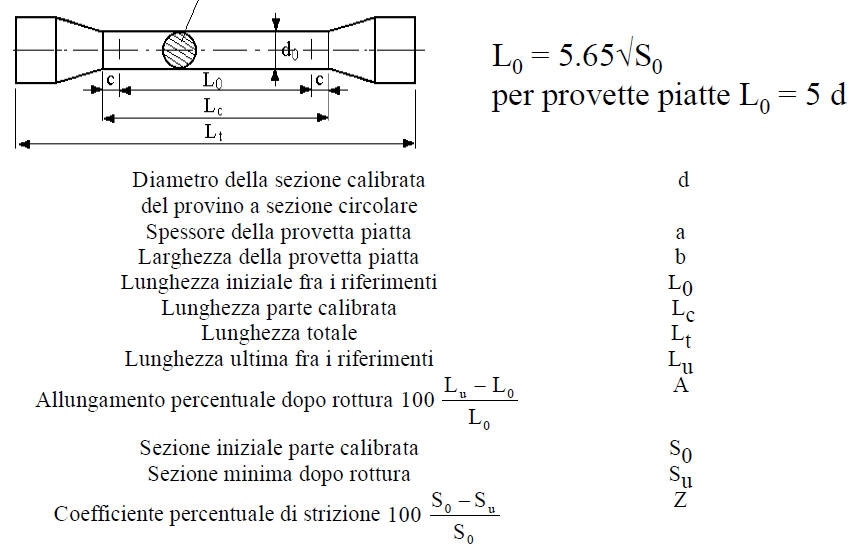
La deformazione corrispondente alla rottura, A, è l'ultimo parametro che si rileva e dipende dalla lunghezza iniziale di riferimento (A senz'altra indicazione corrisponde ad una lunghezza di riferimento pari a 5 diametri).
L'area sotto la curva misura il lavoro fatto, riferito al volume del tratto di riferimento; sino al punto di massimo questo è uniformemente distribuito nel volume.
Nella pratica le sollecitazioni applicate al materiale sono in genere più complesse della semplice trazione.
Il risultato della prova di trazione è utile se si può disporre di un criterio che permette di stabilire che stati diversi di tensione sono equivalenti se hanno eguali certi parametri.
Il criterio più utilizzato, per materiali duttili, detto di von Mises, considera egualmente pericolosi due stati di tensioni che hanno lo stesso lavoro di distorsione, da cui si ricava che la sollecitazione di trazione equivalente è:
![]()
dove s1, s2, s3 sono le tensioni principali.
Il diagramma ricavato nella prova di trazione non rappresenta le tensioni e le deformazioni effettive.
Se si riporta la tensione effettiva, calcolata tenendo conto della variazione della sezione, in funzione della deformazione effettiva, calcolata tenendo conto della variazione di lunghezza, si ottiene una curva con andamento sempre crescente e con pendenza via via decrescente sino alla rottura.
Nella figura 3, è riportato un esempio di criostato per prove di trazione, utilizzato per carichi sino a 100 KN.
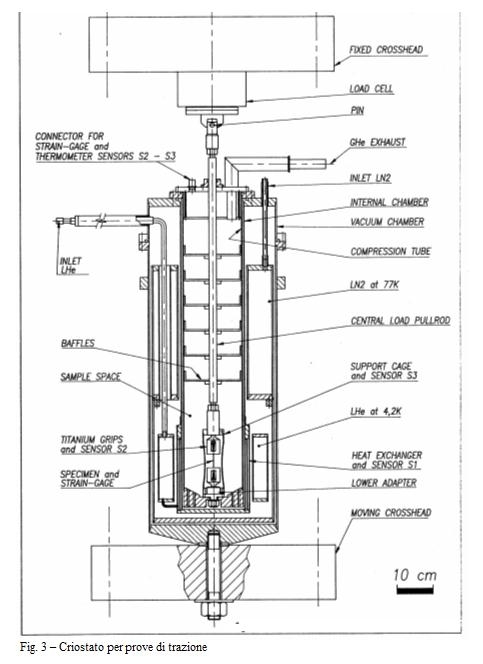
Nelle prove di trazione condotte a temperature comprese tra 4 e 30 K, è possibile osservare una instabilità nella fase di scorrimento plastico, che nel diagramma sforzi deformazioni si presenta come una seghettatura continua, fig. 2.
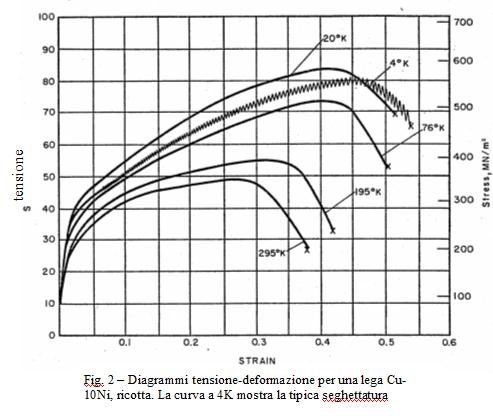
Il fenomeno è presente negli acciai inossidabili, nelle leghe di rame, in alcune leghe di alluminio, nelle leghe di titanio, nel ferro.
Si pensa che un evento iniziatore, (spostamento di dislocazioni, twinning) sia in grado di produrre abbastanza calore da aumentare localmente la temperatura, grazie al basso calore specifico ed alla bassa conducibilità termica (riscaldamento adiabatico). All'aumento di temperatura corrisponde per la deformazione in atto uno sforzo di scorrimento minore, quindi si verifica una diminuzione della tensione ed un aumento della deformazione con ulteriore produzione di calore. Segue un incremento elastico della tensione, una deformazione plastica e un altro evento iniziatore.
La prova analizza gli effetti e raramente le cause: pertanto potrà essere integrata con altre prove, analisi, ricerche.
Esempio: la prova di trazione di un acciaio fucinato può avere rilevato insufficienza di resistenza.
Se la prova è di semplice collaudo, la partita si scarta.
Se la prova è di contestazione, occorre ricercare le cause con altre prove ed analisi.
Nel caso dell'esempio l'insufficienza della resistenza può essere provocata da errata composizione chimica (sostituzione del materiale), da alterazione strutturale per anormale processo di lavorazione (surriscaldamenti, bruciature, decarburazioni, ecc.), da irregolarità o da omissioni di trattamenti termici (temperature e permanenze errate, ambienti non idonei, raffreddamenti non adeguati, cicli non meditati, ecc.).
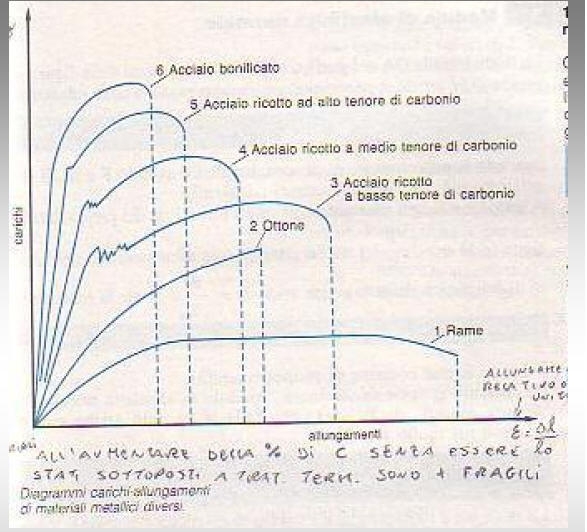
Fm = carico di rottura
Fs = carico di snervamento
σr = Fm/S0 = tensione di rottura
σs = Fs/S0 = tensione di snervamento.
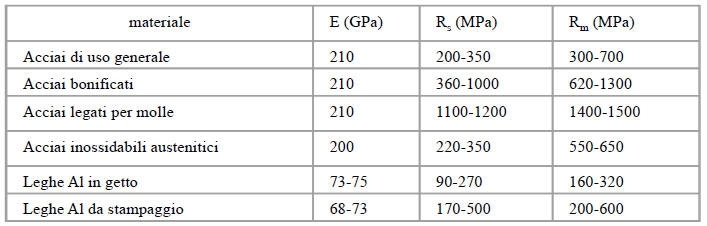
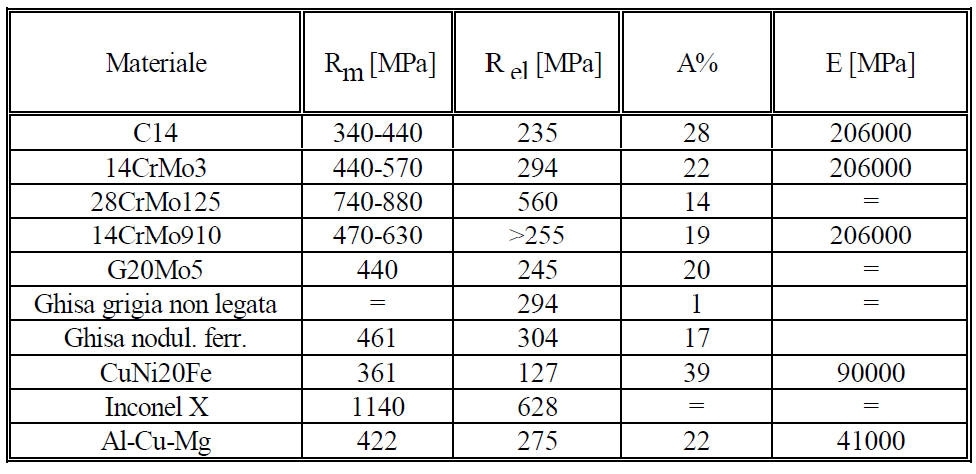
Il grafico ottenuto al termine di ogni prova è caratteristico per ogni materiale.
I trattamenti termici influiscono molto sulla resistenza di un acciaio; anche gli elementi di lega giocano un ruolo fondamentale poichè conferiscono determinate proprietà all'acciaio.

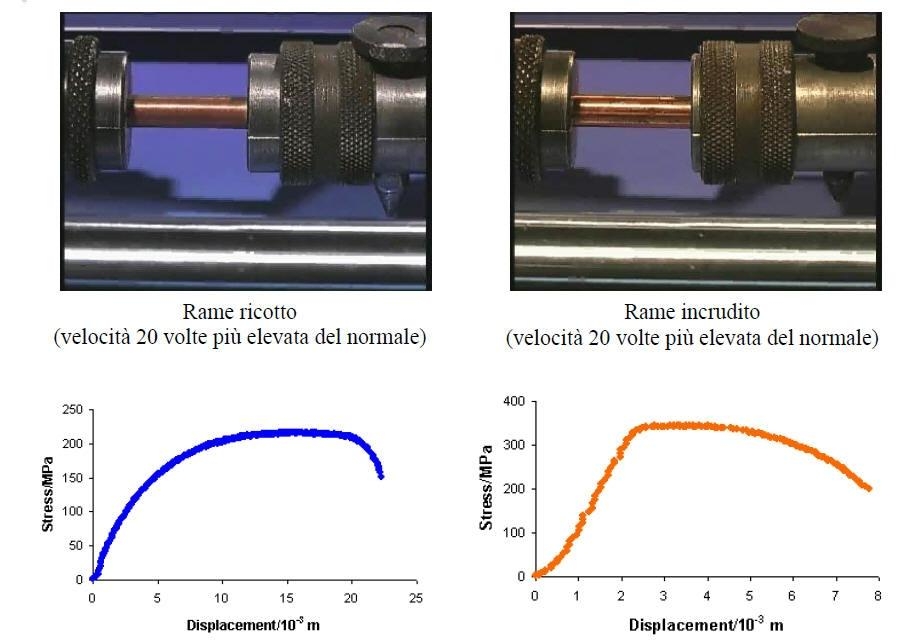
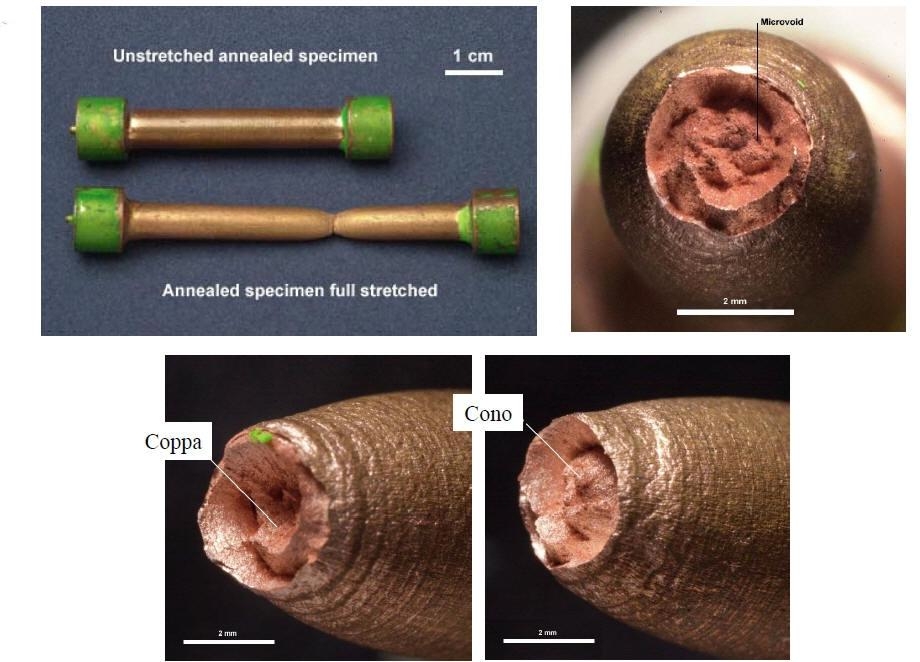

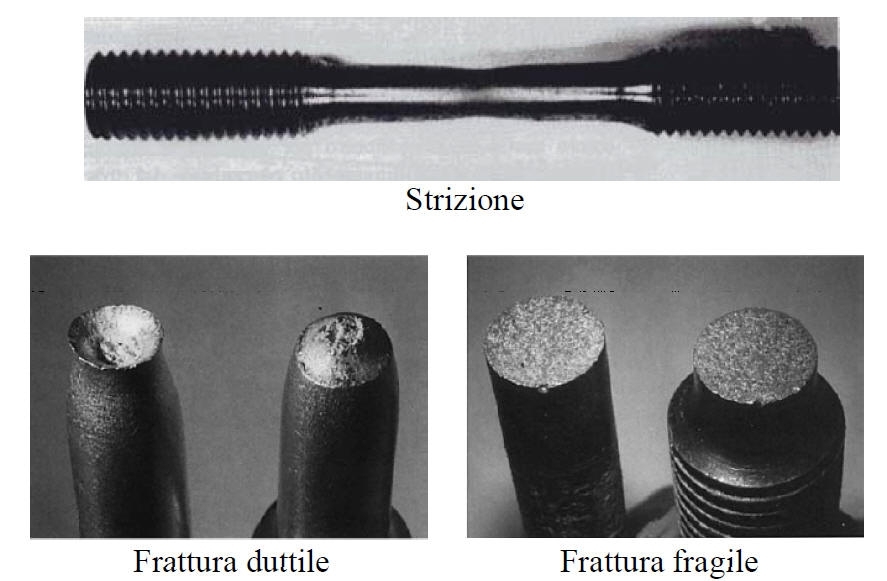

La rottura di un materiale può prodursi per scorrimento con deformazione plastica e assorbimento di energia, per rottura dei legami ad opera di forze parallele al piano di rottura, oppure per separazione delle superfici perpendicolarmente alla forza applicata (clivaggio). Entrambi i modi si verificano secondo piani cristallini preferenziali.
La possibilità che si verifichi l'uno o l'altro degli eventi dipende dal tipo di struttura, dalla temperatura, dalla velocità di deformazione, dalla purezza, etc..
In molti materiali lo scorrimento avviene per sforzi molto inferiori allo sforzo di taglio teorico perchè le dislocazioni possono agire a questi livelli di tensioni. Se questo si può verificare le concentrazioni di sforzi possono essere rilasciate e non si raggiunge mai il livello per attivare la rottura per clivaggio.
Questo è quanto si verifica nei metalli puri del sistema cubico facce centrate.
Nei metalli con struttura cubica corpo centrato ed esagonale compatta è possibile che le dislocazioni siano bloccate e lo scorrimento impedito. In questo caso possono insorgere sforzi di trazione elevati che rendono possibile la rottura per clivaggio.
La prova di trazione su provetta con intaglio serve ad accertare la tendenza di un materiale alla rottura fragile. La provetta, di dimensioni normalizzate, presenta a metà altezza una gola a V con raccordo di fondo molto piccolo. La prova sostanzialmente consiste nel rilevare la forza di rottura alla temperatura richiesta. Per effetto della presenza dell'intaglio la forza di trazione non è uniformemente distribuita nella sezione di gola ma è maggiore sulla circonferenza esterna. Inoltre sono presenti anche tensioni tangenziali e radiali. Lo stato di tensione è triassiale e il rapporto tra lo sforzo di trazione massimo e quello medio (kt, fattore di intensificazione) - 7. Il materiale a lato dell'intaglio, che non raggiunge lo snervamento, agisce come vincolo ed impedisce lo scorrimento. In queste condizioni, nel caso di una piastra con un intaglio profondo, simmetrico a pareti parallele, lo sforzo medio nella gola per produrre lo snervamento risulta, adottando il criterio di von Mises, 2,8 volte lo snervamento rilevato dal provino liscio.
Il modo in cui questo impedimento porta alla transizione tra rottura duttile e rottura fragile è stato descritto da Orowan nel diagramma, riportato in figura 22 dove in funzione della temperatura è riportato lo sforzo di snervamento Y del materiale senza intaglio, lo sforzo di snervamento 3Y del materiale con intaglio (2,8 - stato arrotondato a 3) lo sforzo occorrente per la frattura fragile, che si considera come un processo indipendente sempre possibile e poco influenzato dalla temperatura.
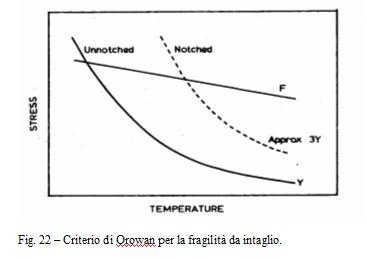
A temperatura ambiente F > 3Y e la frattura è duttile mentre a bassa temperatura - F <Y quindi la frattura è fragile. Vi è un intervallo, in cui Y < F < 3Y nel quale la frattura del provino senza intaglio è duttile e quella del provino con l'intaglio è fragile.
La prova su provino intagliato è stata scelta per la sua semplicità in quanto consente di utilizzare le stesse attrezzature della prova di trazione classica.
E' inclusa ad esempio nella norma di accettazione della lega di Titanio TiAl5Sn2,5, AMS 4924 D, in cui è prescritto che il rapporto tra tensione media di rottura nella sezione di gola e tensione di rottura del provino senza intaglio sia
> 1.Il diagramma ha un significato puramente qualitativo e serve a spiegare come la presenza di stati di tensione triassiali possa modificare il comportamento.
Chiedere che il rapporto non sia inferiore a 1 equivale a chiedere che venga in parte conservata la capacità di adattamento plastico in condizioni di sollecitazioni triassiali.
La prova consiste nel colpire con un pendolo un provino di dimensioni definite nel quale è praticato un intaglio, fig. 23. E' generalizzato l'uso del provino con intaglio a V, profondità 2 mm pareti a 45° raggio di raccordo 0,25. L'energia del pendolo è di 30 Kg x m e si ottiene l'energia assorbita per differenza, misurando l'energia residua dalla risalita del pendolo.
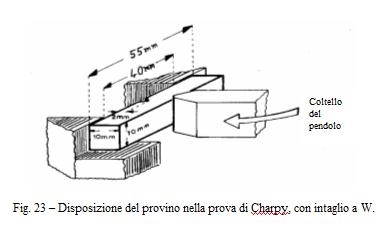
La prova è importante perchè è diventata una delle prove richieste dai regolamenti per l'accettazione dei materiali e dei procedimenti di saldatura, per impieghi a bassa temperatura.
Ad esempio per gli acciai inossidabili è richiesta una prova alla temperatura di esercizio nella quale deve risultare KV > 28J.
Purtroppo l'attrezzatura non è adatta a prove a bassa temperatura e si sono viste soluzioni diverse più o meno valide. Misure a 4 K sono state condotte con il provino chiuso in un piccolo dewar di vetro od in una scatola di materiale isolante, raffreddata da un flusso di vapore di elio. Dal risultato della prova si detrae il contributo del contenitore, rilevato in una prova a parte.
Nella fig. 24 è riportato l'andamento dell'energia assorbita nella prova su un acciaio al carbonio in funzione della temperatura, confrontata con l'allungamento a rottura.
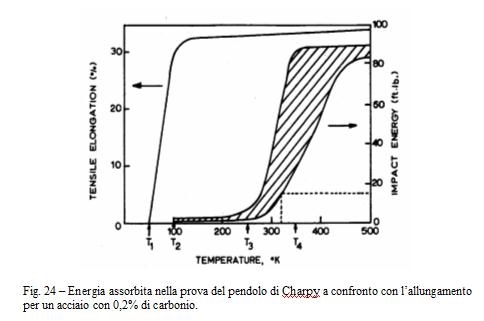
Si vede che a temperatura maggiore di T4 il materiale è tenace e duttile, al di sotto di T1 è senza dubbio fragile, tra T2 e T3 è duttile se deformato a bassa velocità con una sollecitazione monoassiale, ed è fragile se soggetto ad una sollecitazione triassiale applicata ad alta velocità.
Sia la prova con il pendolo di Charpy che quella di trazione su provino intagliato sono prove di confronto. I dati ricavati non sono applicabili ad alcun calcolo di verifica.
In un materiale è molto probabile che si trovino difetti di dimensioni piccole, come microcricche, soffiature, scalfitture.
Concentrazioni molto elevate di tensione possono prodursi al vertice di una microcricca e raggiungere il limite di E/10 necessario per rompere i legami atomici, anche se gli sforzi nominali possono essere molti ordini di grandezze inferiori.
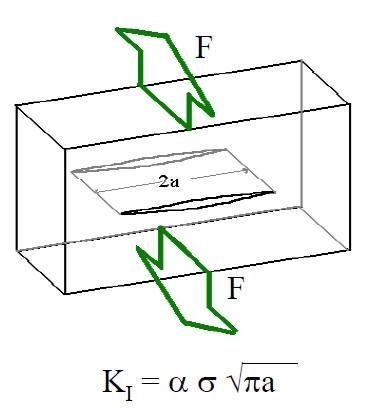
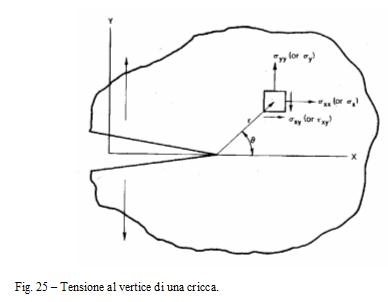
La distribuzione di tensioni intorno al vertice di una cricca, in un materiale perfettamente elastico è data dall'espressione
![]()
vedere fig. 25. Il campo di tensioni è quindi proporzionale ad un fattore K che è funzione dello sforzo applicato, s, della dimensione della cricca a, di una funzione Y(a) dipendente dalla geometria.
La frattura si verifica quando il campo di tensioni al vertice della cricca raggiunge una intensità critica, cioè quando K raggiunge un valore critico Kc, il quale è caratteristico del materiale, è cioè una proprietà meccanica funzione della temperatura, della microstruttura, della velocità di carico.
L'aspetto importante è che K può essere calcolato per diverse geometrie strutturali usando l'analisi delle sollecitazioni.
L'applicabilità del calcolo è estesa al caso che all'apice della cricca vi sia una zona plasticamente deformata, se la dimensione di questa è piccola rispetto alla lunghezza della cricca ed alla sezione netta rimanente. In questo caso si tiene conto della presenza della zona plastica aumentando la lunghezza di una quantità ry
amod = a + ry dove
![]()
dove
sy è la tensione di snervamento al vertice della cricca.La dimensione della zona plastica è influenzata dallo spessore (vedi fig. 26). E'importante che per B > 2,5 (KIc/sys)2 la curva di Kc diventi indipendente dallo spessore, in quanto solo in questo caso risulta essere una caratteristica del materiale.
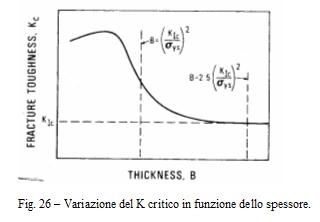
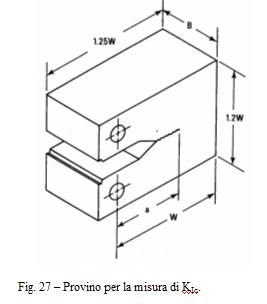
La misura di KIc si ottiene, sottoponendo un provino di dimensioni normalizzate, ved. fig. 27, prima ad una sollecitazione a fatica che produce una cricca la cui lunghezza deve essere compresa entro certe dimensioni e quindi ad un carico crescente sino a rottura rilevando la curva carico apertura.
Il pedice I contraddistingue il modo di rottura, con la forza agente perpendicolare al piano di avanzamento della cricca, che rappresenta il caso più frequente.
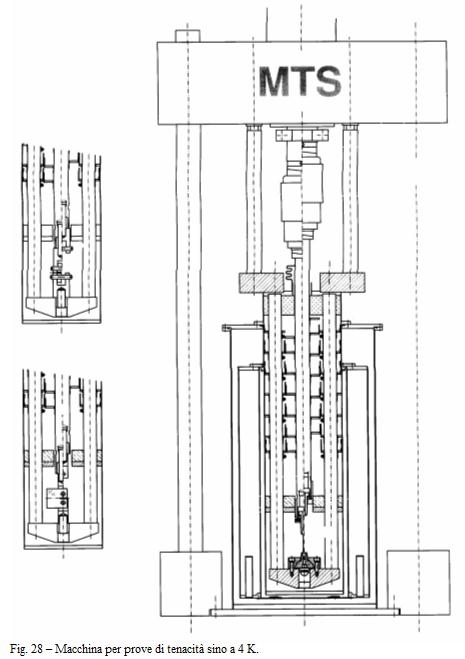
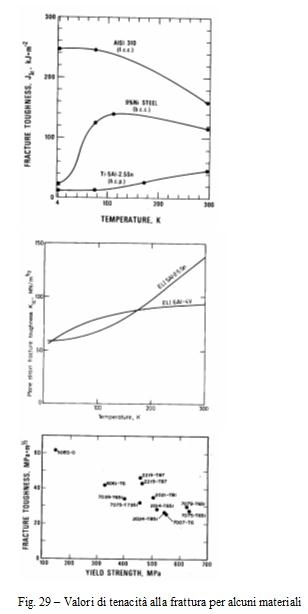
Nella figura 28 è riportato il disegno di una macchina per prove di tenacità sino a 4K. Nella figura 29 sono riportati i valori di KIC per alcuni materiali.
Il fenomeno della rottura per fatica progredisce in tre stadi: la formazione di una cricca, la sua crescita ed infine la rottura.
Quindi la vita di un componente è data dal numero di cicli occorrente per produrre e propagare la cricca sino a raggiungere le dimensioni critiche.
La legge di accrescimento della cricca è data da una relazione del tipo:
![]()
Dove c ed n sono costanti empiriche e
DK è la differenza Kmax - Kmin tra il massimo ed il minimo valore del fattore di intensità dello sforzo.Questo significa che l'avanzamento è dovuto al campo di tensioni ciclico al vertice della cricca individuato da
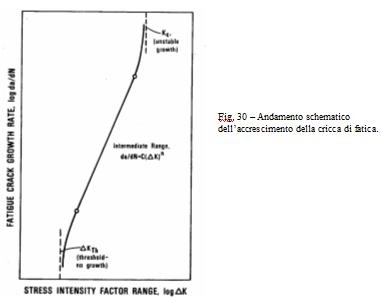
DK. Cioè profilo, frequenza, valor medio del carico sarebbero fattori secondari.La legge da/dN - DK in un diagramma doppio logaritmico è rappresentata da una retta. Vi sono in realtà due limiti uno per bassi DK, rappresenta la resistenza indefinita, senza accrescimento, l'altro per valori di Kmax che si avvicinano al K critico, quando si ha una crescita accelerata. Vedere la. fig. 30.
Nella figura 31 sono riportati dati sull'accrescimento per alcuni materiali di interesse.
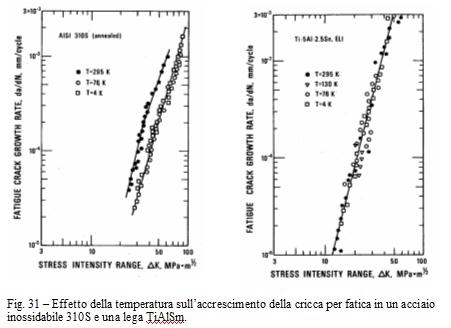
a)
Dimensioni critiche del difettoSi abbia una lastra piana, spessa, di larghezza 2w, che presenta una cricca di ampiezza 2a al centro. Si suppone che il rapporto a/w sia piccolo. Sul lato di ampiezza 2w è applicata una distribuzione uniforme di tensione sl.
L'espressione di K relativa alla geometria considerata è
KI = sl (pa)1/2 . (1 - 0,5 a/w + 0,326 a2/w2)/(1 - a/w)1/2
e per a/w sufficientemente piccolo
K = sl (pa)1/2
al raggiungimento della condizione critica, si ha:
![]()
si abbia: KI,c = 40 MPa . m1/2 e sl = 200 Mpa: risulta acr = 0,013 m
b) La prova in pressione
Un recipiente viene provato ad una pressione superiore a quella di esercizio. Il difetto per il quale la pressione di prova risulta critica abbia dimensione caratteristica apt. Se il recipiente supera il test vuol dire che difetti di quel tipo hanno dimensioni inferiori od eguali ad a pt. Alla pressione di lavoro la dimensione per la quale la pressione risulta critica è maggiore, sia as.
La differenza as - apt è l'accrescimento concesso prima che la condizione di servizio diventi pericolosa. Il tempo corrispondente può essere stimato se si conosce la legge di accrescimento in funzione della variazione del fattore di intensità dello sforzo.
Portale "Ingegneria e
Campanologia" -
Autore -
Sommario
- Mappa del Sito -
Home
Bib-TS-151 - D.A.Wigley "Mechanical properties of materials at low temperatures" Plenum Press 1971
Bib-TS-152 - R.P.Reed and A.F.Clark "Materials at low temperatures" American Society for Metals 1983