Portale "Ingegneria e Campanologia" - Autore - Sommario - Mappa del Sito - Home
Meccanica del mezzo continuo e dei
materiali
AREA I - ARTE TECNICO-SCIENTIFICA (ATS)
Cap. ATS-H01 - Meccanica - Pag. ATS-H01.02
Gli argomenti trattati sono stati inseriti da Ing. Arch. Michele Cuzzoni nel 2012 - © Copyright 2007- 2024 - e sono desunti dalla documentazione indicata in Bibliografia a fondo pagina
Per convenzione si pongono gli indici sempre saturati, cioè:
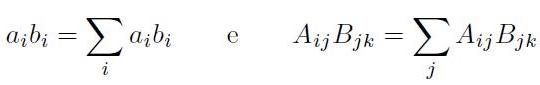[H01-02-01]
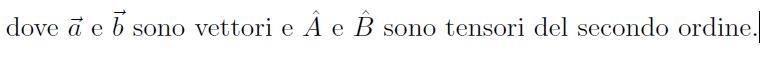
Si consideri un mezzo continuo,
la posizione dei cui punti materiali è riferita, come indicato in Fig.
[H01-02-A]
(sinistra), ad una terna cartesiana e definita dai vettori
.
Quando il mezzo è sottoposto ad una deformazione qualunque, tutti i suoi punti
materiali subiscono uno spostamento nello spazio e le loro posizioni deformate
sono indicate dai vettori
.
Si opera in regime di piccole
deformazioni.
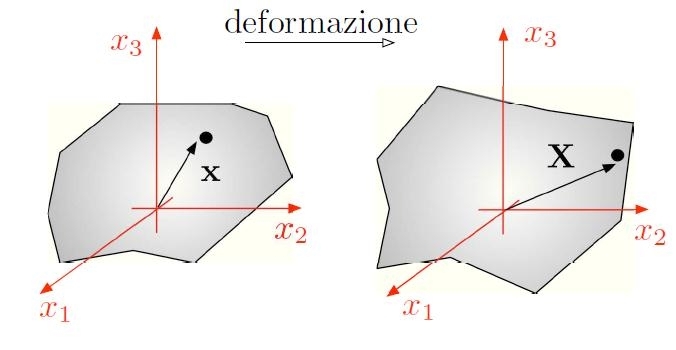
Figura [H01-02-A]: Definizione dei vettori posizione per i punti materiali di un mezzo continuo prima (sinistra) e dopo (destra) l’applicazione di una deformazione.
La relazione generale esistente
tra i vettori
e
si può esplicitare:
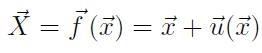[H01-02-02]
dove:
i vettori
rappresentano gli spostamenti e, nel caso generale di un corpo di forma
arbitraria sottoposto ad una generica deformazione, risultano diversi per
ciascun punto materiale. In generale, si avrà quindi:
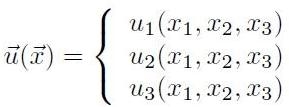[H01-02-03]
La matrice jacobiana
dello spostamento dal sistema dei vettori
a quello degli
è definita da:
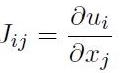[H01-02-04]
La matrice jacobiana
può essere scritta come somma di una parte simmetrica ed una parte
antisimmetrica come segue
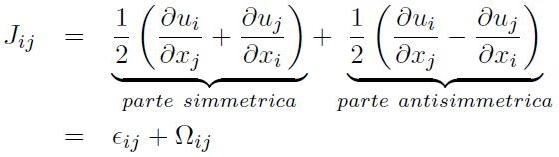[H01-02-05]
con le condizioni evidenti:
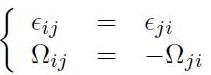[H01-02-06]
Se:
= tensore delle (piccole) deformazioni;
= tensore delle rotazioni locali.
Si può dimostrare che, per una piccola rotazione locale, si ha
e quindi
.
Quindi la forma simmetrica del tensore delle deformazioni è un oggetto che
non tiene in considerazione le rotazioni locali.
Il tensore delle (piccole) deformazioni contiene tutte le informazioni che riguardano localmente la trasformazione geometrica di un corpo e, quindi, deve poter prevedere come variano le lunghezze e gli angoli in ciascuna regione dello stesso. In particolare, si dimostra che:
-
per le variazioni di lunghezza vale:
[H01-02-07]
dove:
-
è la variazione relativa di lunghezza tra due punti interni A e B del corpo
considerato
-
è il versore della distanza A − B.
-
per le variazioni angolari vale:
[H01-02-08]
dove:
-
è il versore della distanza tra due punti A e B
-
è il versore della distanza tra due punti A e C.
L’angolo tra le direzioni
individuate dai suddetti versori è
.
Lo
spostamento
è il campo che descrive in modo completo la deformazione di un corpo.
Si introduce il
tensore
per legare la fisica delle forze di deformazione alla
geometria locale delle deformazioni. Localmente una rotazione non può produrre deformazioni legate all’azione di
forze che si trasmettono in quell’intorno del mezzo materiale. Pertanto, in
teoria della elasticità la relazione che lega le azioni di forze meccaniche alla
deformazione è basata unicamente sul tensore in forma simmetrica:
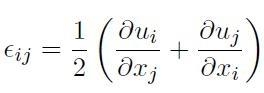[H01-02-09]
Questa definizione `e anche nota come condizione di congruenza.
Si presenta il calcolo esplicito del tensore delle piccole deformazioni in due casi particolarmente semplici.
Si consideri un solido di forma, dimensioni ed orientamento indicati in Fig. [H01-02-B]. Si supponga che esso sia soggetto ad una trazione lungo x1.
Si trascurino tutte le deformazioni nelle direzioni x2 e x3.
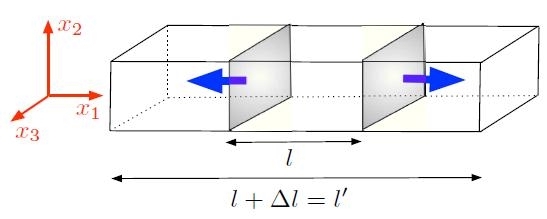
Figura [H01-02-B]: Esempio di trazione semplice.
S
i può calcolare la variazione frazionaria di lunghezza s del solido:
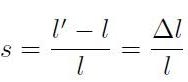[H01-02-10]
in modo tale che la lunghezza
totale dopo l’applicazione della trazione sia
.
Questo ragionamento è ovviamente valido per un qualunque strato interno al
solido, anche se di spessore infinitesimo: lo spessore iniziale
diventerà
per effetto della trazione. Si può scrivere:
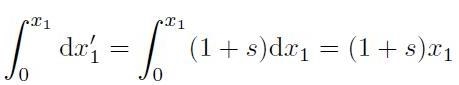[H01-02-11]
da cui è possibile calcolare lo spostamento u1(x1) di uno strato infinitesimo in origine sistemato nel punto x1 come:
[H01-02-12]
Per applicazione diretta della definizione data in Eq. [H01-02-09] si ottiene:
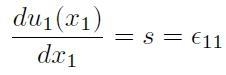[H01-02-13]
tutti gli altri elementi del
tensore
essendo nulli per le ipotesi scelte. In conclusione, si ottiene il tensore delle
deformazioni per una trazione (o compressione) semplice nella forma:
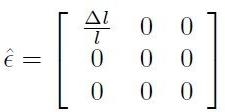[H01-02-14]
Con riferimento alla Fig.
[H01-02-C] si
consideri il caso di un solido, due facce opposte del quale sono spostate di un
tratto
in direzioni antiparallele. Durante questo duplice spostamento si supponga di
mantenere la distanza l tra le due facce inalterata.
In questo caso la variazione frazionaria di lunghezza s lungo la direzione dello sforzo di taglio è:
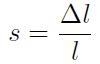[H01-02-15]
cui corrisponde un vettore
spostamento
.
Per applicazione diretta della Eq.
[H01-02-09] si ottiene
il tensore delle deformazioni per un puro taglio nella forma:
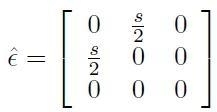[H01-02-16]
Si consideri la situazione in cui un corpo solido è soggetto a forze esterne. Il sistema di forze che complessivamente si instaurano in un solido comprende:
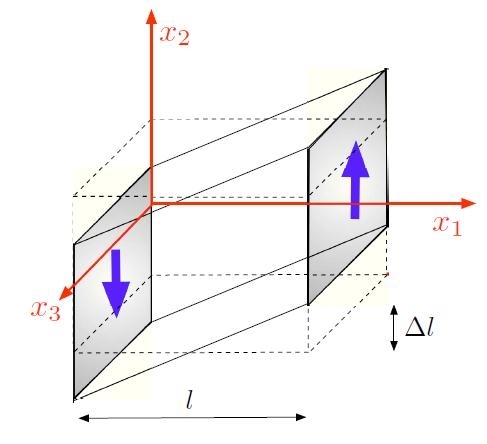
Figura [H01-02-C]: Esempio di sforzo di taglio puro.
-
le forze di volume. Sono dipendenti unicamente dai campi esterni che agiscono sul solido e vengono descritte dal vettore
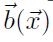che rappresenta la loro densità. Il significato fisico di tale densità si
riassume dicendo che la forza totale
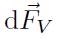applicata ad un piccolo volume dV centrato sul punto
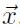è data da
.
Il vettore
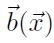rappresenta quindi una forza per unità di volume. Il caso tipico è quello
delle forze gravitazionali che sono proporzionali alla massa della porzione di
volume su cui agiscono.
-
le forze di superficie. Esse sono dovute alle azioni di forza che ciascuna porzione di solido (in Fig. [H01-02-D] indicata dalla porzione interna alla linea tratteggiata) subisce dalla parte rimanente del mezzo continuo (quella esterna alla linea tratteggiata).
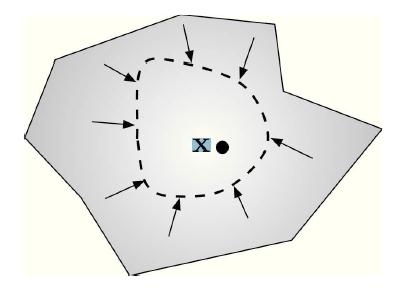
Figura [H01-02-D]: Illustrazione schematica delle forze di superficie che agiscono sul contorno di una qualunque porzione (linea tratteggiata) di corpo solido.
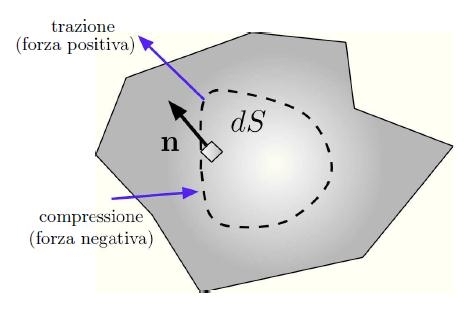
Figura [H01-02-E]: Convenzione sui segni delle forze superficiali di trazione e compressione.
Per convenzione, definito il versore normale uscente
all’elemento di superficie dS, una forza di superficie è negativa se orientata
con verso opposto ad
,
ovvero sia positiva se concorde allo stesso. Dunque, le forze di compressione
sono negative, mentre le forze di trazione (o tensili) sono positive.
La
convenzione è illustrata in Fig.
[H01-02-E]. Risulterà utile introdurre la seguente
notazione per la forza di superficie infinitesima
agente sull’elemento dS:
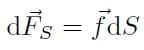[H01-02-17]
dove
assume il significato fisico di una densità di forze per unità di superficie.
E' possibile dimostrare che esiste (ed è unico) un tensore
di rango 3 × 3 tale per cui
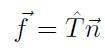[H01-02-18]
Si dimostra, inoltre, che il
tensore
è simmetrico: Tij = Tji. Il tensore
è noto come teorema di Cauchy. Grazie a questo
teorema è possibile scrivere la forza totale di superficie come
[H01-02-19]
ovvero:
[H01-02-20]
Si supponga che
sia diagonale:
[H01-02-21]
(si usa la notazione δij per l’indice di Kroenecker). In questo caso si ricava subito che:
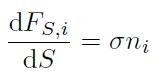[H01-02-22]
e, pertanto, la quantità σ rappresenta la pressione idrostatica (di compressione o di trazione, a seconda del segno di σ ) applicata sul corpo solido.
Si supponga, invece, che il
tensore
sia ora dato nella forma:
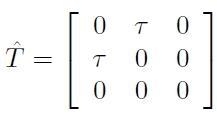[H01-02-23]
dove τ è una quantità nota (detta sforzo di taglio). Si ha:
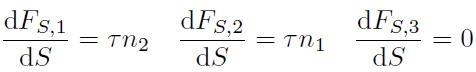[H01-02-24]
che corrisponde all’applicazione di uno sforzo di taglio tangenziale alle superfici dS, con due componenti non nulle parallele, rispettivamente, all’asse di indice 1 e di indice 2.
Se
,
allora
;
analogo risultato vale se
.
Riferendosi alla Fig. [H01-02-F], si può dire che alla faccia numero 2 è applicata una forza per unità di superficie di intensità τ diretta lungo x1 ed alla faccia numero 1 è applicata una forza di intensità τ, ma diretta lungo x2. Entrambe queste forze agiscono quindi tangenzialmente alle facce indicate del cubo. Inoltre, si osservi come l’applicazione di tali forze tenda a trasformare la faccia quadrata numero 4 (o analogamente la 3) in un rombo con l’angolo nell’origine degli assi che è acuto se τ > 0 ed ottuso se τ < 0.
Si conclude
identificando
con il tensore degli sforzi ed attribuendogli il significato fisico di una
pressione vettoriale.
La sua unità di misura è il Pa (si nota che i tipici valori di sforzo che si trovano in meccanica dei solidi variano tra il MPa ed il GPa).
Al fine di meglio comprendere tale attribuzione, si consideri l’elemento di volume cubico riportato in Fig. [H01-02-F]: esso rappresenta una porzione infinitesima dV = (dl)3 di un qualunque corpo solido. Le sei facce del cubo sono numerate secondo la notazione di Voigt.
Qualora
su tale elemento di volume agisca uno sforzo descritto dal tensore
,
le sue nove componenti hanno il significato illustrato in Fig.
[H01-02-G]. La
componente Tij rappresenta la pressione esistente sulla faccia di
indice j ed agente lungo la direzione i.
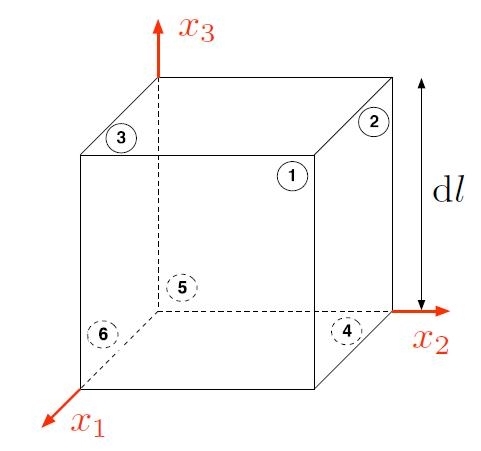
Figura [H01-02-F]: Elemento di volume infinitesimo di un qualunque corpo solido. Le sei facce del cubo sono numerate secondo la notazione di Voigt.
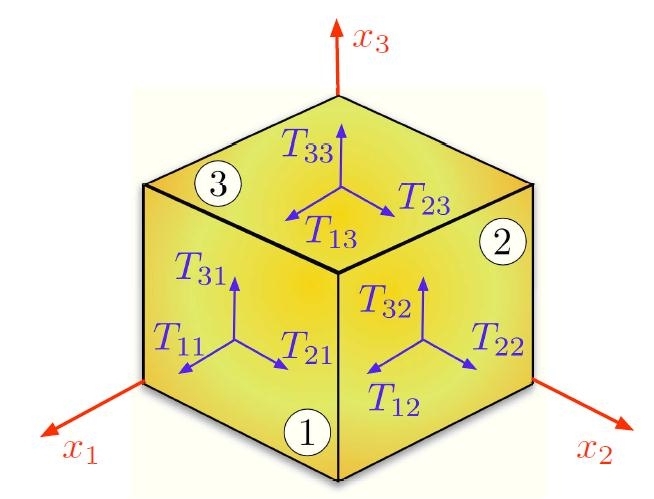
Figura
[H01-02-G]: Significato
geometrico degli indici del tensore degli sforzi
.
Gli oggetti matematici introdotti sono legati da un complesso di quattro equazioni che costituiscono la struttura formale della meccanica del continuo.
Le prime due equazioni – derivate, rispettivamente, dalla prima e seconda equazione cardinale della meccanica razionale – discendono direttamente dal bilancio della quantità di moto e del momento della quantità di moto per un sistema di punti materiali.
In particolare, nel caso statico, esse rappresentano le condizioni di equilibrio traslazionale e rotazionale di un corpo (si ricordi che l’equilibrio si ha quando la risultante delle forze applicate è nulla e la risultante dei momenti applicati è nullo. Esse sono le prime due relazioni fondamentali della meccanica dei continui e possono essere espresse nel seguente modo:
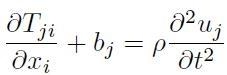[H01-02-25]
e
[H01-02-26]
dove ρ rappresenta la densità volumetrica di massa del mezzo considerato.
La terza equazione è la relazione di congruenza:
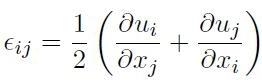[H01-02-27]
La quarta equazione, detta equazione costitutiva, descrive fisicamente la relazione tra la deformazione applicata e lo sforzo risultante (o, equivalentemente, tra lo sforzo applicato e la conseguente deformazione osservata)
[H01-02-28]
La struttura formale della meccanica dei solidi non è in grado di ricavare tale relazione costitutiva che deve essere assunta a priori del problema meccanico di interesse.
Ogni risultato del continuo è profondamente legato alla specifica equazione costitutiva che è stata adottata sulla base della conoscenza fenomenologica del mezzo fisico o sulla base della convenienza formale (o numerica).
Assegnato il più opportuno modello di coesione atomica (empirico o basato su una più rigorosa descrizione delle struttura elettronica del solido considerato), è possibile ricavare in modo esatto (senza ipotesi di convenienza, né su base puramente empirica) la effettiva relazione costitutiva sforzo-deformazione.
L’Eq. [H01-02-28] assume in ogni
punto del solido un’applicazione che associa biunivocamente un tensore degli
sforzi ad un dato tensore delle deformazioni. Durante una deformazione, la
rimozione delle forze esterne applicate comporta il ritorno del solido nelle
condizioni iniziali di stato naturale. Tale stato naturale, o indeformato,
corrisponde ad assenza di sforzi all’interno del corpo (
= 0 se
= 0 e viceversa).
Per molti materiali l’Eq. [H01-02-28] risulta lineare entro certi limiti di deformazione e/o sforzo. Altre volte le equazioni costitutive devono necessariamente contenere termini non lineari (per esempio quadratici e cubici nelle deformazioni) per rappresentare il comportamento reale del mezzo.
Un altro aspetto importante della teoria dell’elasticità riguarda l’ipotesi di piccole deformazioni.
Portale "Ingegneria e
Campanologia" -
Autore -
Sommario
- Mappa del Sito -
Home
Bib-TS-147 - Michele Cuzzoni, Appunti di Scienza
delle Costruzioni - Università degli Studi di Pavia - Facoltà di Ingegneria -
AA. 1995 - 1996
Bib-TS-148 - Michele Cuzzoni, Appunti di Tecnica delle Costruzioni -
Università degli Studi di Pavia - Facoltà di Ingegneria - AA. 1996 - 1997.