Portale "Ingegneria e Campanologia" - Autore - Sommario - Mappa del Sito - Home
Meccanica del mezzo continuo e dei
materiali
AREA I - ARTE TECNICO-SCIENTIFICA (ATS)
Cap. ATS-H01 - Meccanica - Pag. ATS-H01.01
Gli argomenti trattati sono stati inseriti da Ing. Arch. Michele Cuzzoni nel 2012 - © Copyright 2007- 2024 - e sono desunti dalla documentazione indicata in Bibliografia a fondo pagina
Si considera la struttura elettronica di un cristallo secondo l’approssimazione di Born-Oppenheimer, per cui gli atomi del reticolo sono considerati fissi (cioè di massa infinita).
Non si può usare tale approssimazione quando si vogliano considerare i fenomeni connessi al moto o allo spostamento degli atomi del reticolo.
Esistono moltissime proprietà fisiche di un cristallo che dipendono da questi moti, tra cui: la propagazione di onde elastiche, l’assorbimento di radiazione elettromagnetica nella regione dell’infrarosso, la diffusione di elettroni (fenomeno connesso alla resistenza elettrica), i fenomeni di deformazione elastica e plastica.
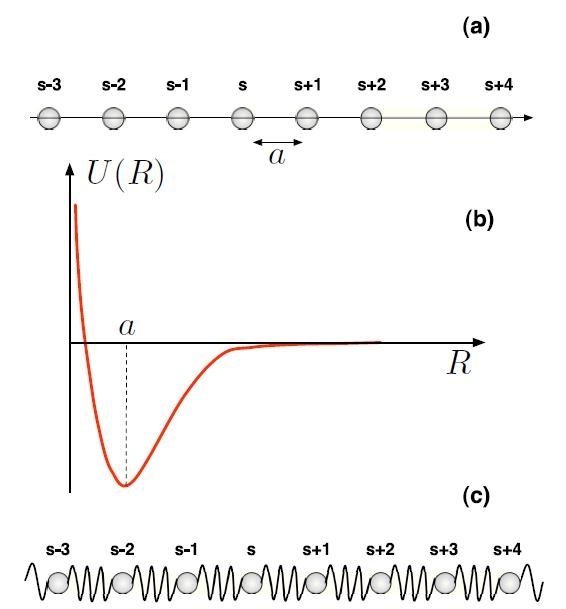
Figura H1-01-A: Schema di cristallo mono-atomico unidimensionale (a); rappresentazione del potenziale interatomico U(R) (b); illustrazione della approssimazione armonica a primi vicini (c).
Si consideri in Fig. H1-01-A una conoscenza elementare dei fenomeni di vibrazione reticolare, basando gli argomenti sul semplice caso di un cristallo mono-atomico (cioè formato da atomi di una sola specie chimica), monodimensionale.
Supponiamo che gli atomi interagiscano tra loro tramite un potenziale U(R), funzione della sola distanza interatomica R. Per piccole oscillazioni longitudinali (cioè per spostamenti lungo la direzione della catena mono-atomica e tali da mantenere ciascun atomo s in un intorno di Rs = sa), si può assumere che le interazioni tra atomi siano di tipo armonico.
Le interazioni sono attive solo tra atomi primi vicini. Essi, dunque, sono collegati da molle (potenziale armonico) di costante elastica pari a λ: queste assunzioni costituiscono la approssimazione armonica (a primi vicini) per la dinamica reticolare.
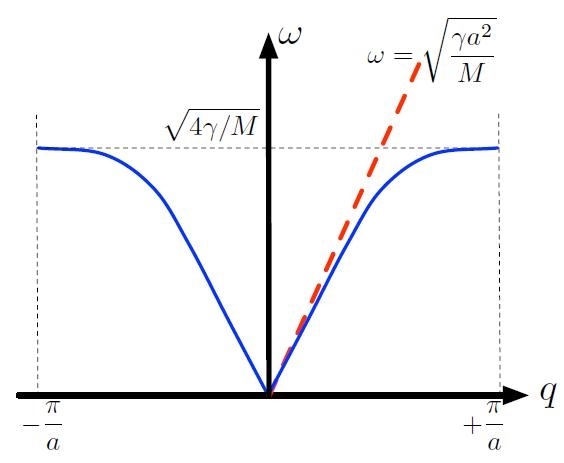
Figura H1-01-B: Relazione di dispersione per vibrazioni armoniche longitudinali in un cristallo mono-atomico monodimensionale (curva continua). Il limite per lunghezze d’onda infinite è rappresentato dalla linea tratteggiata.
L’equazione del moto per il generico atomo in posizione Rs = sa è:
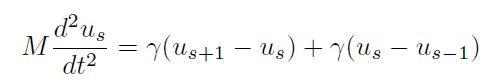[H1-01-01]
dove:
- M è la massa atomica
- us lo spostamento rispetto alla posizione di equilibrio.
Si assuma che lo spostamento us dipenda dal tempo in modo armonico: us ~ exp(−iωt), dove ω è la pulsazione della vibrazione reticolare considerata.
Imponendo, poi, che l’onda vibrazionale sia un’onda piana us = u exp(iqsa) (dove q è il vettore d’onda vibrazionale) si ottiene per sostituzione diretta nella eq. [H1-01-01] la seguente relazione:
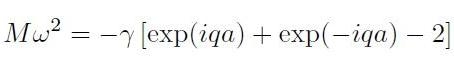[H1-01-02]
che fornisce la relazione di dispersione per le vibrazioni reticolari:
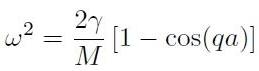[H1-01-03]
Per rappresentare graficamente questa relazione, dobbiamo ricordare che il vettore d’onda q segue le stesse regole del vettore d’onda elettronico k. In altre parole, anche per il vettore d’onda vibrazionale:
- si definisce un reticolo reciproco;
- ci si può limitare a considerare i soli valori di q appartenenti alla prima zona di Brillouin (1BZ) di questo reticolo (Tutti gli altri vettori Q equivalenti - per traslazioni di reticolo reciproco - ad un q Є 1BZ definiscono un identico campo di spostamenti reticolari).
La relazione di dispersione è dunque rappresentata in Fig.[H1-01-B].
Questa condizione equivale a considerare la relazione di dispersione nel limite di vettore d’onda q ® 0 per il quale vale che cos(qa) ~ 1 − 1/2(qa)2. Si ottiene che la relazione di dispersione diventa lineare:
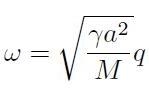[H1-01-04]
come illustrato in Fig.[H1-01-B]. La grandezza:
ha le dimensioni fisiche di una velocità e, pertanto, l’eq.[H1-01-04] rappresenta la relazione di dispersione per un’onda longitudinale acustica, di lunghezza d’onda infinita e propagante nel mezzo con velocità v. Quest’ultima rappresenta la velocità del suono in quel mezzo.
E' evidente che, in questo limite, il fenomeno di propagazione non dipende più dai dettagli reticolari sulla scala atomica (se non per la definizione della velocità v). In altre parole la descrizione del campo di spostamento indotto dall’onda, avviene alla scala macroscopica (coinvolge, cioè modulazioni spaziali su scala molto maggiore delle tipiche distanze interatomiche). Questa conclusione è ulteriormente rafforzata dalla semplice dimostrazione che la legge del moto data in eq.[H1-01-02] si trasforma nel limite q ® 0 nella:
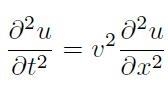[H1-01-05]
dove x individua la direzione di propagazione dell’onda. L’eq.[H1-01-05] `e l’equazione di d’Alembert per la propagazione delle onde meccaniche nei materiali e sottintende una visione del materiale come un continuo.
Questo è proprio la conclusione concettuale importante di questa introduzione: ove si sia interessati a studiare le deformazioni (statiche o dinamiche) di un mezzo materiale su una scala spaziale macroscopica, si può ignorare il dettaglio delle vibrazioni reticolari e considerare il mezzo come un continuo deformabile.
Questa ipotesi di continuità materiale è alla base della teoria della elasticità e della plasticità.
Portale "Ingegneria e
Campanologia" -
Autore -
Sommario
- Mappa del Sito -
Home
Bib-TS-147 - Michele Cuzzoni, Appunti di Scienza
delle Costruzioni - Università degli Studi di Pavia - Facoltà di Ingegneria -
AA. 1995 - 1996
Bib-TS-148 - Michele Cuzzoni, Appunti di Tecnica delle Costruzioni -
Università degli Studi di Pavia - Facoltà di Ingegneria - AA. 1996 - 1997.