Portale "Ingegneria e Campanologia" - Autore - Sommario - Mappa del Sito - Home
Strutturistica Chimica
AREA I - ARTE TECNICO-SCIENTIFICA (ATS)
Cap. ATS-F02 - Chimica - Pag. ATS-F02.19
Gli argomenti trattati sono stati inseriti da Ing. Arch. Michele Cuzzoni nel 2012 - © Copyright 2007- 2024 - e sono desunti dalla documentazione indicata in Bibliografia a fondo pagina
Alla fine della determinazione strutturale e dell’affinamento dei parametri strutturali, si hanno a disposizione:
· Parametri di cella, sistema cristallino
· Simmetria di gruppo spaziale e reticolo di Bravais
· Lista completa delle coordinate atomiche frazionarie per ciascun atomo
· Lista completa dei parametri vibrazionali (termini esponenziali nei fattori di temperatura) che possono essere utilizzati per la stima del movimento atomico nel solido
Come interpretare questi dati, ovvero come posso calcolare la Geometria Molecolare?
Per molecole che cristallizzano in sistemi retti (cubico, tetragonale ed ortorombico) è facile passare a coordinate cartesiane ortogonali (basta moltiplicare le coordinate frazionarie per l’asse corrispondente), ovvero:
Xc = xF*a; Yc = yF*b; Zc = zF*c;
e poi utilizzare la semplice geometria analitica per il calcolo di distanze, angoli e torsioni.
Ma per sistemi non retti (o in generale)?
Trasformazione di coordinate da Frazionarie (xyz) in Cartesiane (X,Y,Z)
X = xa + yb cos
g + zc cosbY = yb sin
g + z{c(cosa – cosb cosg)/sing}Z = zcW/sin
gDove: W2 = (1 - cos2a - cos2b - cos2g + 2 cosa cosb cosg)
Questa trasformazione non è unica!
La scelta proposta genera assi Cartesiani (A,B,C) tali che:
· A è parallelo ad a
· B giace nel piano ab ed è perpendicolare ad a
· C è simultaneamente perpendicolare ad A e B
· Distanze Interatomiche:
Distanza tra A e B: = dA-B ove:
d2
A-B = (XA-XB)2 + (YA-YB)2 + (ZA-ZB)2 =
DX2A-B +
DY2A-B +
DZ2A-B
· Angoli di Legame:
angolo (ABC) = arctan[(1-c2
A)1/2/cA] ove:
cA = -(
DXA-BDXB-C + DYA-BDYB-C + DZA-BDZB-C)/dB-CdA-B
· Angoli di Torsione:
Angolo di torsione (A-B-C-D) = arctan(sT/cT) ove:
sT = (
DXABv1 + DYABv2 + DZABv3)/dABcT = (u1v1 + u2v2 + u3v3)
u1 = (
DYABDZBC - DZABDYBC)/dABdBCu2 = (
DZABDXBC - DXABDZBC)/dABdBCu3 = (
DXABDYBC - DYABDXBC)/dABdBCv1 = (
DYBCDZCD - DZBCDYCD)/dBCdCDv2 = (
DZBCDXCD - DXBCDZCD)/dBCdCDv3 = (
DXBCDYCD - DYBCDXCD)/dBCdCDAlternativamente, senza passare attraverso coordinate cartesiane:
dA-B = [(xA-xB)a]2 + [(yA-yB)b]2 +[(zA-zB)c]2 +
- [2abcos
g(x1-x2)(y1-y2)] - [2accosb(x1-x2)(z1-z2)] - [2bccosa(y1-y2)(z1-z2)]Dato un triangolo di lati AB = l1, AC = l2 e BC = l3, l’angolo BAC =
d può essere calcolato con la legge dei coseni:cos
d = (l21 + l2
2
- l23)/2l1l2
Esempi di semplici calcoli di parametri geometrici:
NaCl cristallizza nel sistema cubico, gr. spaziale Fm3m; a = 5.6402(2) Å.
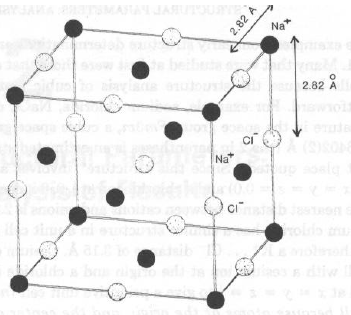
Le posizioni atomiche indipendenti sono
Na in 0.00 0.00 0.00
Cl in 0.50 0.00 0.00
Data la simmetria di gruppo spaziale, esistono 4 atomi di Na in cella, in
0, 0, 0; 0, ½, ½; ½, ½, 0; ½, 0, ½
Data la simmetria di gruppo spaziale, esistono 4 atomi di Cl in cella, in
½, 0, 0; 0, ½, 0; 0, 0, ½; ½, ½, ½;
Quanto valgono le dNa-Cl e dCl-Cl più corte?
dNa-Cl = ½ a = 2.820 Å; dCl-Cl =
Ö2/2 a = 3.988 ÅPer KCl (dalla stessa struttura cristallina: KCl e NaCl sono isomorfi), a = 6.2931(2) Å, da cui dK-Cl = ½ a
» 3.15 Å; dCl-Cl » Ö2/2 a = 4.45 ÅPer CsCl (struttura cubica primitiva Pm3m), a = 4.120(2) Å)
Cs in 0.00 0.00 0.00
Cl in 0.50 0.50 0.50
dCs-Cl =
Ö3/2 a = 3.568 ÅSi deduce quindi, nell’approssimazione di sfere rigide, che i raggi ionici degli ioni dei metalli alcalini e degli alogenuri seguono un andamento regolare (di gruppo).
A seconda dei modelli utilizzati e del numero di coordinazione,
r(Na+) = 0.95-1.17 Å; r(K+) = 1.33-1.49 Å;
r(Cl-) = 1.64-1.81 Å; r(F-) = 1.16-1.36 Å
Per la specie FeS2 la cella cubica ha a = 5.4175(5) Å, gruppo spaziale Pa3:
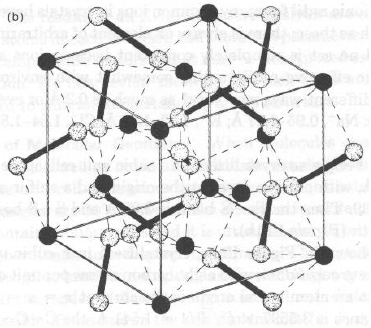
Fe in 0.00 0.00 0.00
S in x x x x = 0.39
Data la simmetria di gruppo spaziale, esistono 4 atomi di Fe in cella, in 0, 0, 0; 0, ½, ½; ½, ½, 0; ½, 0, ½
Data la simmetria di gruppo spaziale, esistono 8 atomi di S in cella, in ± ( x,x,x; ½+x, ½–x; -x; -x, ½+x; ½-x; ½-x, -x, ½+x) x=0.39
per Fe in 0,0,0 e S in x,x,x:
dFe-S = a * [(0.39-0.00)2 + (0.39-0.00)2 +(0.39-0.00)2 ]1/2 = 3.65 Å
ma anche:
con S in ½+x, ½–x; -x; (0.89, 0.11, -0.39) cioè (-0.11, 0.11, -0.39)
dFe-S = a * [(-0.11-0.00)2 + (0.11-0.00)2 +(-0.39-0.00)2 ]1/2 = 2.27 Å (x6)
S1 in x,x,x (0.39, 0.39, 0.39); S2 in 1-x, 1-x, 1-x (0.61, 0.61, 0.61)
e dS-S = a * [(0.61-0.39)2 + (0.61-0.39)2 +(0.61-0.39)2 ]1/2 = 2.06 Å
Per il diamante (C), cella cubica a = 3.5597 Å e gruppo spaziale Fd3m.
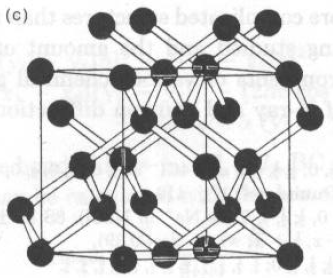
C in 0., 0., 0.
Data la simmetria di gruppo spaziale, esistono 8 atomi di C in cella, in:
0,0,0; 0,½,½; ½,0,½; ½,½,0;
0.25,0.25,0.25; 0.25,0.75,0.75;
0.75,0.25,0.75; 0.75,0.75,0.25;
La distanza minima C-C è per:
dC-C = a * [(0.25-0.00)2 + (0.25-0.00)2 +(0.25-0.00)2]1/2 =
Ö3/4 a = 1.541 ÅC-C-C = 109.5° e: C-C-C-C = 60° o 180° (a seconda di qual è il 4° C)
In generale, le strutture studiate oggigiorno sono molto più complesse (fino a 200-300 atomi indipendenti) ed il calcolo dei parametri geometrici è effettuato in modo automatico, tenendo conto delle costanti di cella, degli operatori di simmetria di gruppo, delle traslazioni reticolari e delle coordinate frazionarie determinate per via diffrattometrica.
Sono attualmente note
· più di 200.000 strutture che contengono un atomo di carbonio (organiche e di coordinazione), Cambridge Crystallographic Data File
· diverse decine di migliaia di strutture ‘inorganiche’ (
Inorganic Crystal Structural Database, Karlsruhe, Germania)· alcune migliaia di strutture di metalli, leghe e composti intermetallici (Pearson Handbook)
· alcune migliaia di strutture di oligonucleotidi e proteine (
Protein Data Bank, Brookhaven, NY)Struttura cristallina del benzene (a bassa temperatura!):
Sistema: Ortorombico
Gruppo Spaziale: Pbca
Cella: a = 7.44, b = 9.55, c = 6.92 Å
Atomi in ± (x,y,z; ½+x,½ -y,-z; -x,½+y, ½-z; ½-x,-y,½+z)
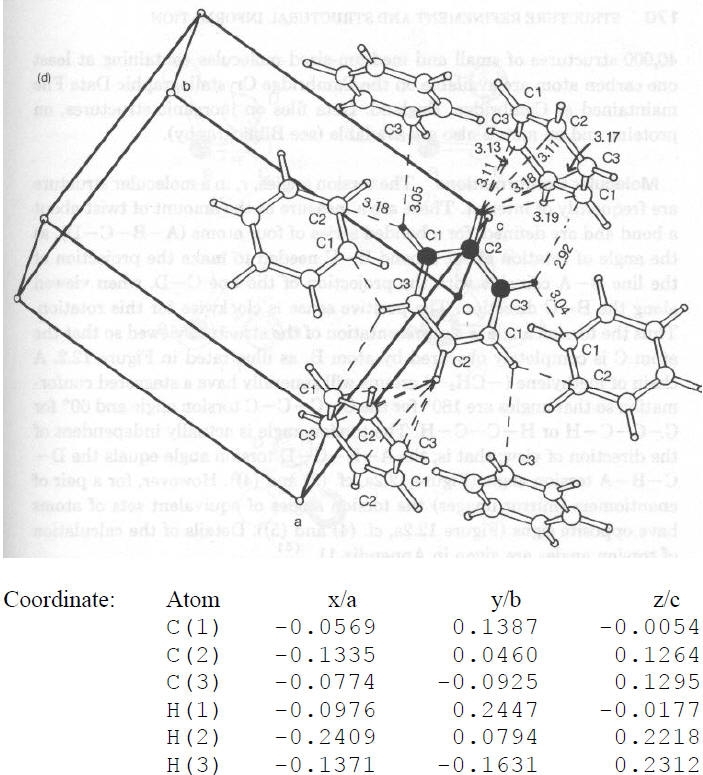
Per un sistema retto: dA-B = [(xA-xB)a]2 + [(yA-yB)b]2 +[(zA-zB)c]2
· dC1-C2 = {[(-0.0569+0.1335)*7.44]2 + [(0.1387-0.0460)*9.55]2 + [-0.0054-0.1264)*6.92)2}1/2 = {0.3248 + 0.7837 + 0.8318}1/2 = 1.393 Å
In molecole non-rigide, spesso la stereochimica è caratterizzata da un ben preciso set di angoli di torsione,
t, che sono· la misura della torsione attorno al legame B-C nella sequenza A-B-C-D;
· la misura dell’angolo diedro formato tra i piani definiti da ABC e BCD
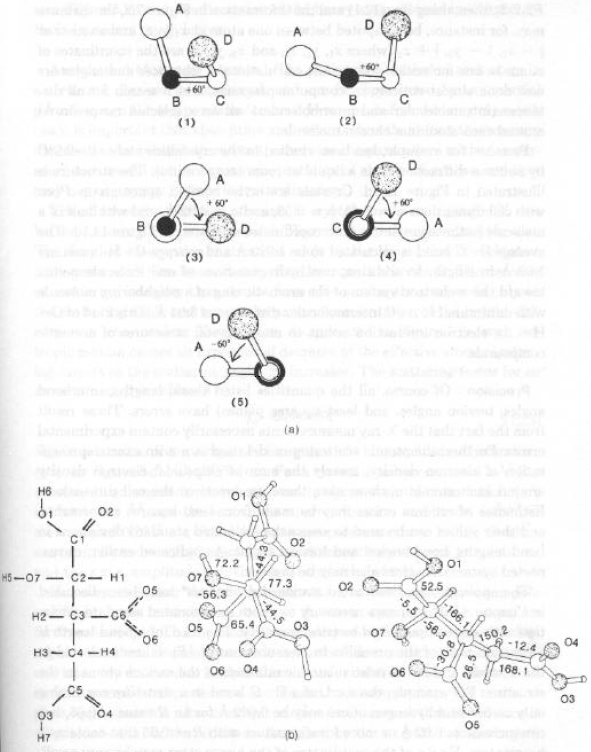
Il senso positivo di una torsione è dato da una rotazione oraria. Sono definiti in [-180°; 180°]
La sequenza opposta D-C-B-A possiede torsione con lo stesso valore assoluto e segno.
Due enantiomeri hanno distanze ed angoli identici ma torsioni
uguali ed opposte.Gli alcani lineari con atomi C(sp3), tipicamente hanno conformazione
zigzag [C-C-C-C sfalsati, t = 180° e C-C-C-H e H-C-C-H con t ± 60°)Esempi:
· (1-4) diverse viste dello stesso gruppo di atomi con torsione di +60°
· (5) gruppo di atomi enantiomerico con torsione –60° Ovvero: 4 e 5 non sono sovrapponibili (simmetria puntuale C2)
· Ione Isocitrato:
1) formula di struttura; 2-3) struttura molecolare con angoli di torsione
Altri parametri geometrici utili:
· Piano ai minimi quadrati (ovvero quel piano ‘migliore’ che passa vicino a 4 o più atomi, ciascuno dei quali ne dista una ben definita quantità); è spesso utilizzato per confrontare molecole, conformazioni e presenza di coniugazione in anelli, etc.
· Angoli diedri: torsioni tra piani molecolari
· Baricentri: punti ideali per la definizione di enti geometrici ausiliari quali assi, perni, etc.
Distanze Intermolecolari:
· Distanze tra atomi non legati, appartenenti ad unità molecolari diverse, che si trovano adiacenti nel cristallo grazie ad operatori di simmetria del gruppo e traslazioni reticolari.
· Se ci sono diverse molecole ‘indipendenti’ nell’unità asimmetrica, alcune distanze intermolecolari si possono calcolare senza l’ausilio del gruppo spaziale.
· Permettono di evidenziare particolari interazioni significative, come legami ad idrogeno, stacking p-p, interazioni acido-base, agostiche, etc.
Esempio: nel benzene cristallino a –55°C, si osservano distanze intramolecolari di legame C-H di 1.07 Å (diffrazione di neutroni…), e distanze intermolecolari C…H di 3.04 Å, indicative di un’interazione
C-H…elettroni p, tipica di composti aromatici.· Permettono anche si evidenziare presenza di cavità (zeoliti, nanopori, canali, etc.) o suggeriscono la presenza di molecole di solvente clatrato non evidenziato per via diffrattometrica
· Valori particolarmente corti (ed atipici) devono far sospettare problemi nel modello o effetti di disordine
Precisione ed Accuratezza: Ogni misura sperimentale ed ogni quantità da essa derivata è soggetta ad errori casuali e sistematici.
La precisione assegnata ad un valore ne indica la coerenza interna, ovvero la ripetibilità nelle stesse condizioni sperimentali, e non tiene conto degli errori sistematici. Essa esprime la larghezza
DX di una distribuzione (gaussiana?) intorno ad un valor medio <X>. <X> ± DXAttenzione: <X> , in presenza di errori sistematici, può essere molto lontano dal valor
vero XV.L’accuratezza, di solito molto inferiore alla precisione, ne indica la riproducibilità in sistemi, luoghi ed esperimenti differenti, e dovrebbe tener conto della presenza degli errori sistematici. Può essere normalmente stimata solo da ripetute misure interlaboratorio, magari con tecniche differenti, fatte solo in casi particolari.
· Spesso di parla di deviazioni standard (e.s.d.), che rappresentano una stima della precisione. Esse dipendono dalla precisione nella misura degli |Fo| (riflessa da R) e dai numeri atomici relativi delle specie in esame.
· P.es.. In una struttura puramente organica (in assenza di atomi pesanti come metalli o Br, I, etc.) un valore R = 0.05 può garantire esd di 0.002 Å, mentre in un composto metallorganico, lo stesso R può risultare in esd(C-C) di 0.02 Å (o più).
· La posizione assoluta di un atomo con tanti elettroni (atomo pesante) è molto più precisa di atomi ‘leggeri’.
· La posizione assoluta di un atomo che vibra poco (al centro della molecola) è molto più precisa di atomi della ‘periferia’.
L’entità e la direzione dei diversi moti atomici e molecolari, per lo più associati a vibrazioni ( e raramente a librazioni – rotazioni impedite – o traslazioni) modifica in modo sostanziale l’intensità diffratta.
In presenza di sole vibrazioni, per un modello isotropo armonico, il fattore di scattering atomico frest(sin
q/l) cambia in: fvib = frest exp[-Biso(sinq/l)2] e comporta la diminuzione dell’ampiezza diffusa ad alti angoli (il cristallo diffrange meno..) Biso = 8p2<u2> » 79<u2>dove <u2> è la media del quadrato dell’ampiezza di vibrazione.
·
A temperatura ambiente e per sistemi molecolari (non ionici) Biso sono intorno a 4 Å2, il che comporta <u2> » 0.05 Å2 o <u2>1/2 » 0.22 Å (15% di una distanza C-C)·
A bassa T (100 K, » p.e. azoto liquido), di Biso » 1 Å2, e <u2>1/2 » 0.12 Å (8% di una distanza C-C)Misure di diffrazione a bassa T comportano un aumento dell’intensità diffratta, un numero maggiore di riflessi osservati e, quindi, maggior precisione nei parametri geometrici derivati.
In presenza di sole vibrazioni, per un modello anisotropo armonico, il fattore di scattering atomico frest(sin
q/l) cambia in:fvib = frest exp[-(b11h2 + b22k2 + b33l2 + b12hk + b23kl + b31hl]
e, come nel caso isotropo, comporta la diminuzione dell’ampiezza diffusa ad alti angoli, ma in modo vettoriale, non scalare.
fvib = frest exp[-(
HBHT)] con H = [h,k,l]· Il tensore simmetrico B rappresenta un ellissoide a 3 assi di semiassi con termini diagonali bii>0
· I termini fuori dalla diagonale ne danno l’orientazione rispetto agli assi di cella.
· Spesso si utilizza il tensore U, tale per cui:
Uii = bii/2
p2a*i2 e: Uij = bij/4
p2a*ia*j ( i ¹ j )· Con dati di diffrazione molto accurati, è possibile studiare moti vibrazionali complessi (per esempio lungo un arco, o non armonici). In generale, con buoni dati di diffrazione si riescono a determinare parametri vibrazionali anisotropi solo per atomi con Z > 4 (dal B in su).
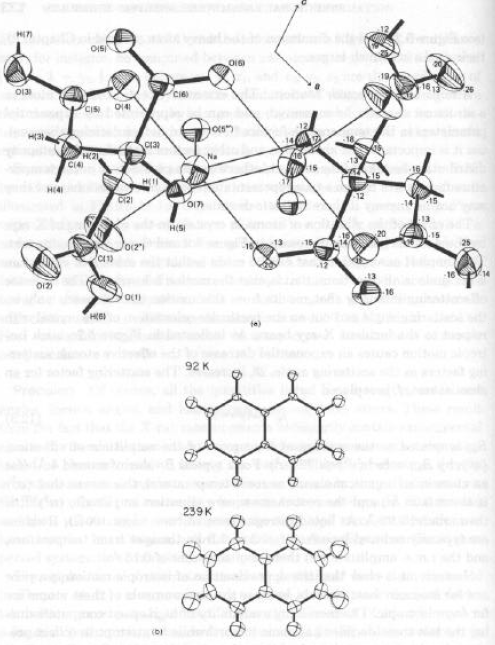
Rappresentazione grafica (modello ORTEP – Oak- Ridge Thermal Ellipsoid Plot, C.K.Johnson).
Effetto della temperatura di raccolta dati sulle dimensioni (ed orientazione) dei parametri termici.
Alcune molecole posseggono contemporaneamente moti vibrazionali (limitati) e moti più complessi che mantengono le posizioni relative degli atomi costanti.
Esempio: rotazione di un fenile in PPh3 attorno al legame P-Cipso; In questo caso, i parametri termici determinati non sono interpretabili come vibrazioni, ma come librazioni (in qualche caso addirittura traslazioni) di un frammento intero.
· E’ possibile, con dati di alta qualità, determinare separatamente il moto di corpo rigido da quello vibrazionale.
· In presenza di dati di mediocre qualità, è tuttavia utile approssimare un frammento a un ‘corpo rigido’, trascurandone le vibrazioni interne e riducendo drasticamente i parametri affinabili. (Una sola terna xyz, ed una sola terna Rx,Ry,Rz + tensore Ucorpo-rigido)
Conseguenze stereochimiche di un’errata interpretazione o mancata osservazione di fenomeni di librazione sono un incorretta determinazione delle distanze di legame intramolecolari (che appaiono troppo corte, specialmente se perpendicolari ad assi con elevata librazione),
Esempi: Carbonili Terminali, trans-Stilbene
Esistono tecniche numeriche di ‘correzione’, noti i pattern di vibrazione..
Tipicamente questa è una pesante sorgente di errori sistematici, normalmente trascurati.
La radiazione associata a neutroni ‘monocromatici’, ovvero di velocità fissa e nota (v), è determinata dalla relazione di De Broglie:
l = h/pDato che EK = ½mv2 = p2/2m
l = h/[2mEK]1/2È possibile effettuare diffrazione di neutroni se scegliamo opportune sorgenti (EK ca. 1-1000 meV), monocromatori e rivelatori (alcune decine di strumenti al mondo..)
Ci sono importanti differenze con i raggi X:
· I neutroni interagiscono con nuclei puntiformi e non con densità elettronica (diffusa).
· I neutroni ‘sentono’ la presenza di nuclei diversi (anche di isotopi).
· Il fattore di diffusione (b = scattering length) è molto piccolo: per avere intensità diffusa misurabile devo utilizzare cristalli di alcuni mm di dimensione.
· Il fattore di diffusione non dipende da sinq/l: si osserva alta intensità anche ad alto angolo (a parte le vibrazioni termiche..).
· Il fattore di diffusione b può anche essere negativo (H) o nullo (V)
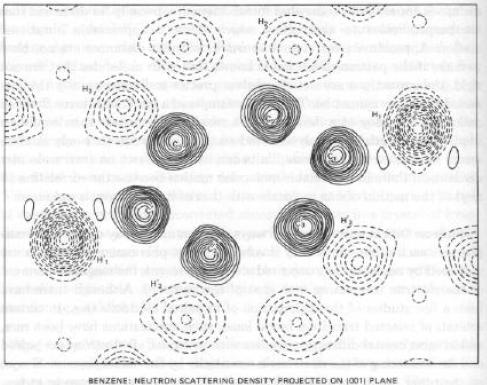
Densità di Scattering Neutronico per un cristallo di benzene analogo della Densità Elettronica per esperimenti di diffrazione di Raggi X
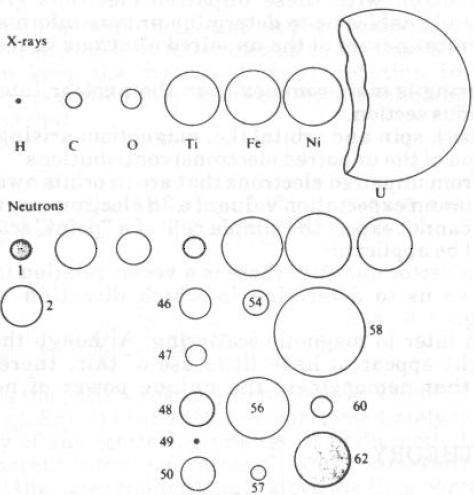
· Il fattore di diffusione non dipende in modo sistematico da Z. Ciò permette di studiare atomi ‘leggeri’ invisibili ai raggi X quando sono presenti atomi ad alto Z (es. Fe, Co, Ni)
· Si possono anche distinguere atomi adiacenti che hanno b molto diversi e Z pressoché uguali. Si possono distinguere isotopi in oggetti marcati, es. H,D)
· Dato che i neutroni vedono i nuclei e i raggi X gli elettroni, per gli atomi che non hanno elettroni di core (p.es. H), saranno localizzati in ‘posti differenti’, p.es. a ca 1.07 Å (N) e 0.95 Å (X) da un atomo di carbonio
sp3.· Dato che i neutroni posseggono spin ½, è possibile avere scattering magnetico da parte di spin ‘elettronici’ spaiati (studi a bassissima T)
· I neutroni non vengono (quasi) mai assorbiti: non ci sono errori sistematici legati all’assorbimento od alla diffusione anomala (tranne in qualche caso come 6Li). E’ addirittura possibile studiare campioni all’interno di contenitori stagni (criostati di acciaio, celle di pressione..)
Dato che la densità elettronica di legame è poco concentrata, ovvero molto diffusa, i suoi effetti si fanno sentire soprattutto a bassi valori sinq/l, ovvero laddove sono spesso predominanti errori sistematici.
Se però misuro dati ad alta risoluzione (alti angoli), grazie ad un raffreddamento spinto, all’utilizzo di cristalli non difettuali, di radiazioni molto penetranti (bassa l), di rivelatori veloci per collezionare il numero più elevato possibile di riflessi, allora:
· La posizione degli atomi ed i loro parametri termici sono ben determinati dai (numerosi) dati ad alto angolo. Ogni deviazione sperimentale dei dati a basso angolo è interpretabile come effetto di valenza.
(Metodo X-X: Mappa di Fourier differenza tra tutti i dati sperimentali e quelli calcolati da un modello ottimizzato sugli alti ordini (X))
· Se conosco le posizioni ed i B di tutti gli atomi in modo indipendente (diffrazione da neutroni), allora qualsiasi deviazione dei dati di diffrazione di raggi X (a qualsiasi angolo) può essere interpretata come effetto di valenza.
[Metodo X-N: Mappa di Fourier Differenza tra tutti i dati sperimentali (X) e quelli calcolati da un modello ottimizzato da diffrazione di neutroni (N)].
· E’ possibile sviluppare modelli multipolari in cui il fattore di scattering atomico, non più scalare, è vettoriale, ed è la trasformata di Fourier di un atomo non-sferico.
Portale "Ingegneria e
Campanologia" -
Autore -
Sommario
- Mappa del Sito -
Home
Bib-TS-081 - Prof. N. Masciocchi - Dispense del Corso di Laurea in Chimica - Insegnamento di strutturistica chimica
Bib-TS-082 - C.Hammond - The Basics of Crystallography and Diffraction - Ed. International Union of Crystallography and Oxford University Press, 240 pg. (Ed. italiana: Zanichelli)
Bib-TS-083 - J.P.Glusker & K.N.Trueblood - Crystal Structure Analysis: A Primer - Oxford University Press, 220 pg. (non tradotto).