Portale "Ingegneria e Campanologia" - Autore - Sommario - Mappa del Sito - Home
Strutturistica Chimica
AREA I - ARTE TECNICO-SCIENTIFICA (ATS)
Cap. ATS-F02 - Chimica - Pag. ATS-F02.17
Gli argomenti trattati sono stati inseriti da Ing. Arch. Michele Cuzzoni nel 2012 - © Copyright 2007- 2024 - e sono desunti dalla documentazione indicata in Bibliografia a fondo pagina
Problema: Quant'è l'ampiezza diffusa da un singolo elettrone?
Problema: Quant'è l'ampiezza diffusa da un gruppo di elettroni?
Problema: quant'è l'ampiezza diffusa da una collezione di atomi (molecola, cella unitaria, etc..)?
Problema: come è la distribuzione delle intensità di un cristallo acentrico?
1. Diffusione elastica: interazione tra onda e particella (Thomson)
2. Diffusione inelastica: interazione tra due particelle (Compton)
- Raggi X - Densità elettronica r(r)
- Elettroni - Potenziale elettrostatico F(r(r))
- Neutroni - Densità nucleare r=(r)
Qualunque essa sia (calcolabile e/o misurabile), la prendiamo come unità di riferimento.
E' la somma su tutti gli elettroni, tenendo conto che le onde diffuse hanno ampiezza e fase, e quindi differenze di cammino ottico e fasi.
Per N elettroni in un atomo, questo valore è il fattore di scattering atomico
fattore di scattering atomico f = ampiezza diffusa da un atomo / ampiezza diffusa da un singolo elettrone.
Ad angolo di diffrazione nullo (q = 0), tutte le onde diffuse sono in fase, ed il valore di f è uguale al numero di elettroni nell'atomo neutro f = Z
Ad angoli di diffrazione diversi da zero, ci saranno alcune interazioni fuori fase tra onde con cammino ottico diverso e f sarà minore di Z.
f dipende da q (o senq/l = d*/2), in modo scalare da d* (nel reciproco)
Tipicamente, i fattori f sono calcolabili e tabulati per incrementi successivi in senq/l, o messi in grafico.
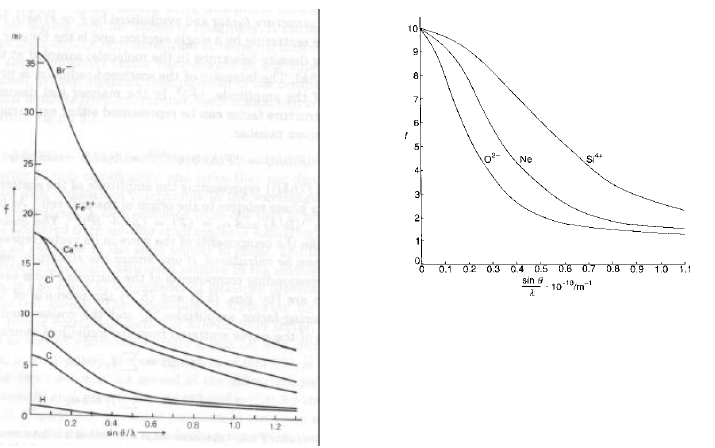
Per O2-, Ne, Si4+ (tutti con 10 elettroni totali), le curve mostrano che:
- Atomi o ioni grossi hanno grossa dipendenza angolare di f
- Atomi o ioni piccoli hanno minor dipendenza angolare di f
Basta sommare i diversi contributi atomici tenendo conto delle differenze di cammino ottico (fasi diverse).
Per una cella unitaria, F è il fattore di struttura:
fattore di struttura Fhkl = ampiezza diffusa da tutti gli atomi in cella / ampiezza diffusa da un singolo elettrone
I pedici hkl indicano l'ampiezza della radiazione diffusa per un certo piano reticolare con indici di Laue hkl (e quindi Fhkl dipendono vettorialmente nello spazio reciproco)
Fhkl = numero complesso, che contiene un'ampiezza ed una fase!
La determinazione di una struttura cristallina per diffrazione di raggi X consiste in una serie di passaggi, tra i quali:
1. Misura della posizione angolare e dell'intensità diffratta nello spazio.
2. La determinazione della forma e delle dimensioni della cella cristallina (dedotta dalle posizioni dei picchi di diffrazione nello spazio reciproco)
3. La determinazione della posizione degli atomi nella cella a partire dalla misura delle intensità Ihkl di tutti i riflessi.
Le parti 1 e 2 sono generalmente sperimentalmente e matematicamente accessibili, mentre la 3, tenuto conto che Ihkl = |Fhkl|2 (ove si perdono informazioni sulle fasi), richiede la ricostruzione della fase per ciascun riflesso, tramite una serie di ipotesi, calcoli, statistiche, intuizione matematica e conoscenza cristallografica e chimica.
Utile per la comprensione di base, ma praticamente impossibile da trattare in sistemi complessi in più dimensioni.
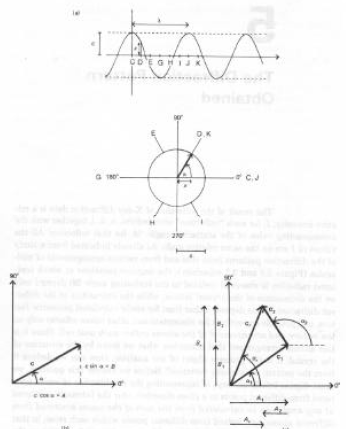
Una qualsiasi onda può essere rappresentata da funzioni trigonometriche:
Onda #1: x1 = c1 cos(f + a1)
Onda #2: x2 = c2 cos(f + a2)
ci sono le ampiezze di ciascun'onda;
xi i valori "spostamento" punto per punto,
ai le fasi relative
f (uguale per ogni onda), è un valore proporzionale al tempo (per un'onda che si propaga).
Assunzione: le onde hanno la stessa lunghezza d'onda l (radiazione monocromatica e diffusione elastica).
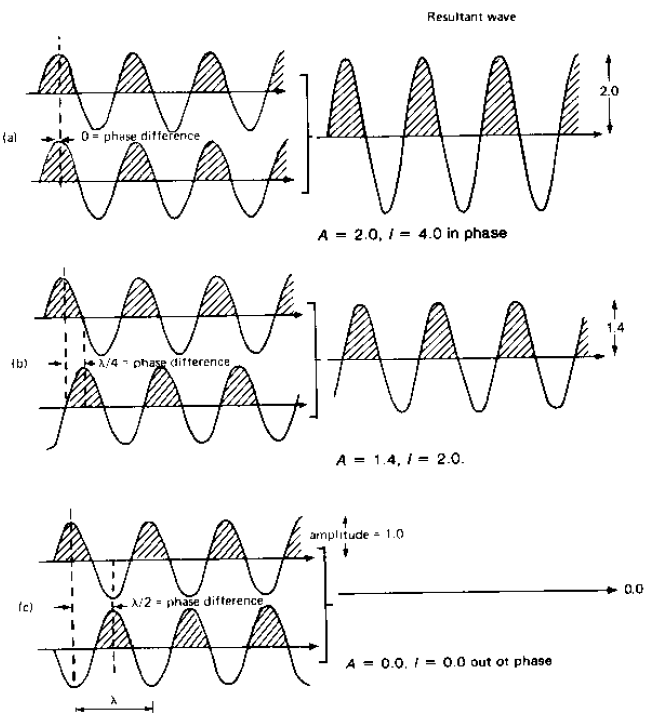
La sovrapposizione di onde genera un'onda (risultante) caratterizzata da spostamento xr = x1 + x2
Quindi: xr = x1 + x2 = c1 cos(f + a1) + c2 cos(f + a2)
Ovvero: xr = c1 cosf cosa1 - c1 senf sena1 + c2 cosf cosa2 - c2 senf sena2
xr = cosf (c1 cosa1 + c2 cosa2 ) - senf (c1 sina1 + c2 sena2)
Se definiamo, per l'onda risultante, cr ed ar in modo che:
-
cr cosar = c1 cosa1 - c2 cosa2 = Sj cj cosaj-
cr senar = c1 sena1 + c2 sena2 = Sj cj senaj- xr = cos
f (cr cosar) + senf (cr senar) = cr cos(f + ar)
L'onda risultante dalla somma di due (o più onde) dalla stessa frequenza e di ampiezze ci e fasi ai, possiede ampiezza cr e fase ar date da:
tan
ar = cr sinar / cr cosar = Sj cj senaj / Sj cj cosaj e:cr = [(cr cos
ar)2 + (cr senar)2]1/2 = [(Sj cj cosaj)2 + (Sj cj senaj)2]1/2
Lavorando, p.es. nel piano xy, è possibile sommare onde come se fossero vettori di lunghezza ci e fase (angolo con l'asse x) ai:
Le componenti x ed y sono, rispettivamente, Ai = ci cosai e Bi = ci senai
L'onda risultante è caratterizzata dalla somma di vettori ed è equivalente alla descrizione algebrica precedente.
Nel piano complesso (di Gauss-Argand) un vettore di componenti A (sull'asse reale) e B (sull'asse immaginario) è descritto da un punto P (numero complesso P) del tipo:
P = (A,B) coppia ordinata di numeri reali o:
P = A + iB
- Il complesso coniugato P* è il numero P* = A - iB
- Il modulo di P, |P| è un valore reale dato da |P| = [PP*]1/2 = [(A + iB)(A - iB)]1/2 = [A2 - i2B2]1/2 = [A2 + B2]1/2
Esprimendo P = A + iB in notazione esponenziale:
- P = |P|eif , dove f è l'angolo di fase dato da tanf = B/A derivata dalla relazione: eif = cosf + isenf
Siano ora: A = cr cosar = Sj cj cosaj B = cr senar = Sj cj senaj cr = (A2 + B2)1/2
Per l'onda risultante, A + iB = cr cosar + icr senar = creiar
La somma di diverse onde di tipo cjeiaj
creiar = Sj cjeiaj
non è altro che una somma di numeri complessi!
- Si prenda un cristallo bidimensionale caratterizzato da una ripetizione ordinata di atomi "singoli" (ciascuno di fattore di scattering f0), ciascuno localizzato all'origine della "cella".
- Sia il cristallo in condizioni di diffrazione, tale per cui l = 2dhklsinq
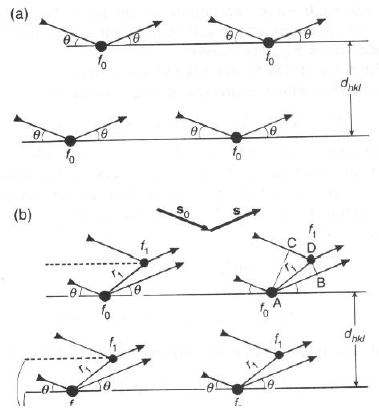
- Per gli atomi che giacciono nello stesso piano, la differenza di cammino ottico tra i raggi diffratti è nulla, e gli atomi diffrangono in fase.
- Per gli atomi che giacciono in piani separati di dhkl, 2dhkl, etc., per costruzione (dato che vale la legge di Bragg!), la differenza di cammino ottico �
l, 2l, etc., ed ancora gli atomi diffrangono in fase.
- In ambedue questi casi, l'ampiezza diffusa totale è FTOT = S f0
- Per ogni cella, c'è un unico atomo (all'origine) e l'ampiezza diffusa per cella, Fhkl - Fhkl = f0
- Il cristallo non contiene solo un atomo per cella, ma un "motivo molecolare" costituito da 2 atomi uguali (p.es. cristallo di I2, etc.)
- Per costruzione, mettiamone uno all'origine e l'altro in posizione r1.
- r1 può essere descritto da coordinate frazionarie (u1, v1, w1) tali per cui: r1 = ruvw = u1a + v1b + w1c
- La differenza di cammino ottico tra le onde diffuse da questi atomi è: DC.O. = AB � CD = r1 .s - r1 .s0 = r1 .(s -.s0)
Ricordandoci che:
r1 = ruvw = u1a + v1b + w1c
e che, essendo soddisfatta la legge di Bragg:
. (s -.s0) = ld*hkl = l (ha* + kb* + lc*)
DC.O. = l (ha* + kb* + lc*) . (u1a + v1b + w1c)
Moltiplicando e semplificando (a.a* = 1, a.b* = 0, etc.):
DC.O. = l (hu1 + kv1 + lw1)
- Il numero (hu1 + kv1 + lw1), che rappresenta la componente di r1 perpendicolare ai piani dhkl in "frazioni di dhkl", è il parametro fondamentale che caratterizza le condizioni di interferenza costruttiva / distruttiva.
- Se (hu1 + kv1 + lw1) = 0 [gli atomi giacciono nello stesso piano di indici hkl], si ha interferenza costruttiva.
- Se (hu1 + kv1 + lw1) = 0.5 [gli atomi giacciono uno nel piano di indici hkl e l'altro esattamente a metà tra i piani], si ha interferenza distruttiva.
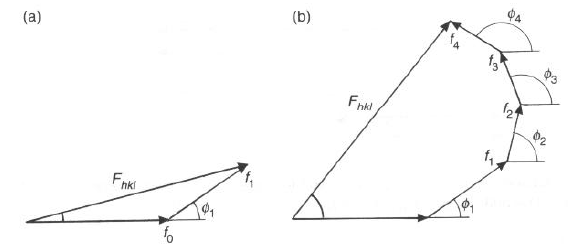
Nel caso generale, in cui ci siano più atomi, ciascuno di fattore di scattering atomico fi, in posizioni caratterizzate da ri, basta usare un diagramma vettoriale, da cui si ricava che:
definendo fi = 2p/l DC.O. = 2p(hu1 + kv1 + lw1)
l'onda risultante è caratterizzata da:
Fhkl = S fi exp [2pi (hui + kvi + lwi)]
Con:
- (ui, vi, wi) coordinate frazionarie (POSIZIONI) degli atomi in cella
- 2p(hui + kvi + lwi) angolo di fase fi dell'atomo i-esimo
- Fhkl = fattore di struttura (complesso) del riflesso di indici di Laue hkl (che determina l'intensità del raggio diffratto)
In pratica, esiste una relazione matematica tale per cui,
- nota la metrica della cella reale (da cui si ricava quella reciproca)
- nota la posizione di tutti gli atomi in cella (ui, vi, wi)
Si può calcolare la grandezza Fhkl = |Fhkl|eif e, noto |Fhkl|, calcolare |Fhkl|2, che è proporzionale all'intensità diffratta del "riflesso" di indici hkl.
Per la notazione: Fhkl = A + iB
A =
S fi cos [2p (hui + kvi + lwi)]B =
S fi sen [2p (hui + kvi + lwi)]f
= tan-1 B/AEsempio #1: Struttura del CsCl
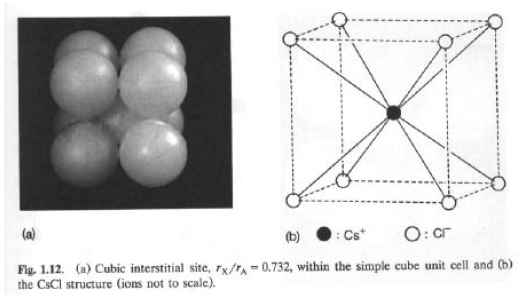
Le posizioni atomiche sono (uCl, vCl, wCl) = (0, 0, 0)
(
uCs, vCs, wCs) = (-, -, -)da cui:
Fhkl =
fCl exp[2pi(h0+k0+l0)] + fCs exp[2pi(h'+k'+l')] == =
fCl + fCs exp[pi(h+k+l)]I caso: (h+k+l) = intero pari = 2n; exp[2n
pi] = 1; Fhkl = fCl + fCsII caso: (h+k+l) = intero dispari = 2n+1; exp[(2n+1)
pi] = -1; Fhkl = fCl - fCs
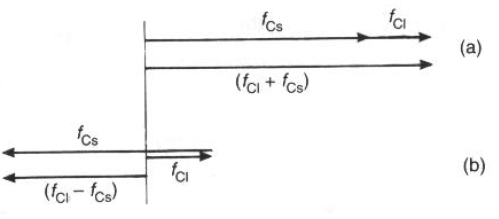
In ambedue i casi i valori Fhkl sono valori reali (componente immaginaria nulla): questo è valido ogniqualvolta la struttura ha un centro di simmetria all'origine della cella!
Esempio #2: Struttura di un metallo hcp (cella primitiva esagonale)
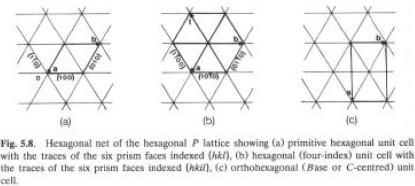
Le posizioni atomiche sono:
(
uA, vA, wA) = (0, 0, 0)(
uB, vB, wB) = (1/3, 2/3, 1/2)Fhkl = f exp[2
pi(h0+k0+l0)] + f exp[2pi(h1/3+k2/3+l1/2)] = f [1 + exp[2pi(h1/3+k2/3+l1/2)]
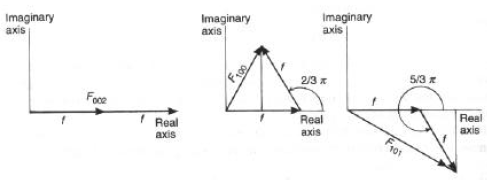
Qualche esempio:
- Piano (002)
F002 = f [1 + exp(2
pi)]= 2f- Piano (100)
F100 = f [1 + exp[2
pi(1/3)]] = f [1 +cos(2/3p) + isen(2/3p)] = f (0.5+i0.866)- Piano (101)
F101 = f [1+exp[2
pi(1/3+1/2)]]= f [1+cos(5/3p)+isen(5/3p)] = f (1.5-i0.866)Le intensità, proporzionali a |Fhkl|2, saranno date da:
I002 = 2f.2f = 4
f2I100 = [f (0.5+i0.866)][f (0.5-i0.866)] =
f2I101 = [f (1.5-i0.866)][f (1.5+i0.866)] = 3
f2
N.B. Le intensità sono numeri reali anche se Fhkl sono complessi. La misura sperimentale delle intensità non permette la determinazione della fase associata ad ogni riflesso.
Esempio #3: Realtà dei fattori di struttura di cristalli centrosimmetrici (con l'origine sul centro di simmetria)
- Per ogni atomo di coordinate frazionarie (uA, vA, wA) ce n'è uno di coordinate frazionarie (-uA, -vA, -wA)
- Per ogni atomo con angolo di fase +f, ce n'è uno con angolo di fase -f
- Per ogni coppia di atomi centrosimmetrici, Fhkl = f exp [2pi (huA+ kvA + lwA)] + f exp [2pi (-huA - kvA - lwA)] =
= f exp [2pi (huA+ kvA + lwA)] + f exp [-2pi (huA+ kvA + lwA)] = somma di un complesso col suo coniugato: i termini in seno spariscono:
Fhkl = 2f cos [2
p (huA+ kvA + lwA)] numero reale- Sommando su ogni coppia di atomi si sommano numeri reali Fhkl = SN/2 fi cos [2p (hui + kvi + lwi)]
Corollario: la distribuzione delle intensità diffratte da un cristallo centrosimmetrico è anch'essa centrosimmetrica.
Per un solo atomo in cella, calcoliamo separatamente I(+h+k+l) e I(-h-k-l)
I(+h+k+l) = F(+h+k+l) F*(+h+k+l) = f exp[2
pi(hu+kv+lw)] f exp[-2pi(hu+kv+lw)] = f exp[2pi(hu+kv+lw)] f exp[2pi(-hu-kv-lw)]I(-h-k-l) = F(-h-k-l) F*(-h-k-l) = f exp[2
pi(-hu-kv-lw)] f exp[-2pi(-hu-kv-lw)] = f exp[2pi(-hu-kv-lw)] f exp[2pi(hu+kv+lw)]Ovvero: F(+h+k+l) = F*(-h-k-l) e F*(+h+k+l) = F(-h-k-l), da cui: I(+h+k+l) = I(-h-k-l)
La distribuzione delle intensità diffratte da un cristallo, centrico od anche acentrico, è sempre centrosimmetrica
- N.B. Se e solo se f è reale (in assenza di assorbimento..)
- In presenza di assorbimento, f = f0 + f' + if' (f ' complesso, ma f' è di solito piccolo..): la legge di Friedel è (quasi) vera..
- Le correzioni f' ed f' sono i fattori di diffusione anomala: non dipendono da sinq/l, ma dall'energia della radiazione incidente.
- La presenza di un centro di simmetria nella distribuzione delle intensità, qualsiasi sia la simmetria reale del cristallo, implica che gruppi puntuali non centrosimmetrici non possono essere distinti da quelli centrici
- Dei 32 gruppi puntuali cristallografici, solo 11 contengono un centro di simmetria: sono i cosiddetti gruppi Laue
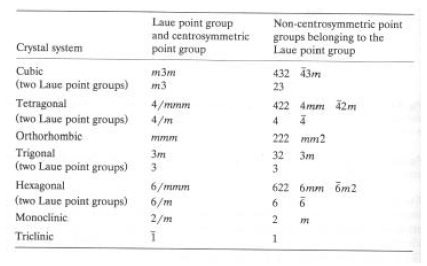
- Esistono comunque tecniche più raffinate (scattering anomalo) o di analisi statistica delle intensità che permettono "ipotesi" di simmetria centrica od acentrica.
In pratica:
- La misura delle Ihkl permette di calcolare |Fhkl|, ma non la sua fase.
- Nota la struttura, è possibile calcolare |Fhkl|, la sua fase, ed Ihkl
- Determinare la struttura = vuol dire assegnare la fase a ciascun riflesso per cui si è misurata Ihkl
- Tipicamente, si raccoglie un numero alto di Ihkl (1000-100000), per poi risolvere la struttura (risolvendo il problema della fase) per molecole di 10 - 200 atomi circa.
In prima approssimazione: Ihkl = k |Fhkl|2
In realtà: Ihkl = k |Fhkl|2(Lp)(Abs)
Dove:
- (Lp) è un fattore trigonometrico conosciuto (e che dipende dal tipo di strumento), che tiene conto della velocità (angolare) di scansione w (detto fattore di Lotentz L o fattore cinetico) e della polarizzazione indotta da un eventuale monocromatore (p). (Lp) è indipendente dalla struttura cristallina.
- (Abs) è un fattore di attenuazione dei raggi primario e diffratto dovuto all'assorbimento (tipo Lambert-Beer I = I0 exp-mx che va integrato su tutto il volume del cristallo per tutti i differenti cammini ottici). (Abs) dipende fortemente dalla forma e dalle dimensioni del cristallo e dalla sua composizione chimica. Solo per cristalli sferici la correzione dipende solo da q (ovvero da d*hkl, e non è vettoriale..).
-
|Fhkl| in realtà è il fattore di struttura per atomi a riposo, |Fnovib|. Dato che ad ogni temperatura, tutti gli atomi si muovono, se <u2> è lo spostamento quadratico medio per un moto armonico isotropo intorno alla posizione di equilibrio (in -2):|Fhkl| = |Fnovib| exp(-Bisosin2
q/l2) e Biso = 8p2<u2> (in -2)- Tipicamente, a T ambiente cristalli ionici hanno 0.5 < Biso < 2.0
- Tipicamente, a T ambiente cristalli molecolari hanno 3.0 < Biso < 6.0 Biso = 3.5 significa <u2>1/2 di 0.21 - (10-15% di d(A-A) 1-2.5 )
- Ovvero, ad alto q (>25è con tipica radiazione Mo-Ka), cristalli ionici mostrano intensità diffratta e cristalli molecolari no!
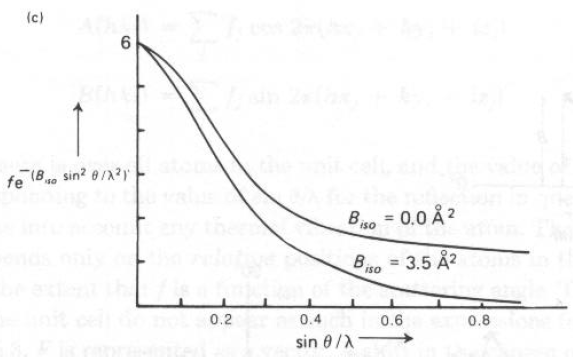
Quindi, il valore "corretto" di Ihkl che dipende solo dalla struttura e dal movimento degli atomi, ma non dall'esperimento e dalla forma e dimensioni del campione è:
Icorr = Ihkl/(Abs)(Lp) = k |Fhkl|2
- Se riusciamo a stimare k (Metodo di Wilson o Wilson Plot, che stima anche un <B> medio), possiamo misurare:
|Fhkl| = (Icorr/k)1/2 in scala assoluta (elettroni!), che è uno degli ingredienti fondamentali per tentare di assegnare le fasi e risolvere la struttura.
Dalle formule viste, in ogni nodo del reticolo reciproco, esiste un'intensità diffratta che contiene il contributo di tutti gli atomi in cella, in termini di specie atomica (fj), coordinate (ujvjwj) e moto termico (<B> o Bj).
1. Diversamente dai cristalli ideali, hanno dimensioni finite
2. Il numero di celle contigue è "limitato"
Dalla teoria della diffrazione ottica:
- La larghezza dei picchi principali dipende da quanto è grande N (numero di righe in un reticolo, o numero di fenditure)
- Se N non è particolarmente grande, compaiono minimi e massimi secondari, tanto più importanti quanto è basso N
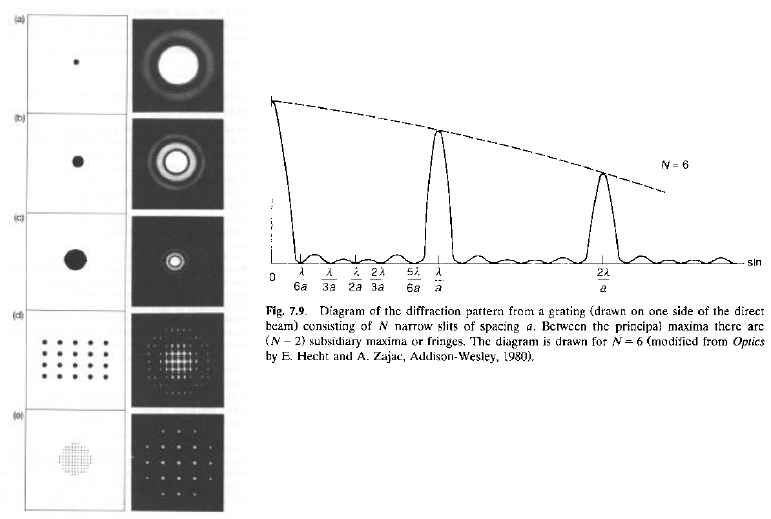
- Per la diffrazione di raggi X, se N è piccolo, i punti reticolari in cui si ha diffrazione non-nulla sono dei "nodi con dimensione"; pertanto, essi attraversano la sfera di Ewald non "istantaneamente" (all'angolo q), ma a anche a valori angolari leggermente diversi (q + dq)
- Cristalli piccoli (tipicamente <1 mm) hanno picchi allargati. Rispetto alla risoluzione strumentale (dqS) , il picco ha una larghezza effettiva (sperimentale) dqE = dqS + dqC [dqC = dqC(Campione)] o, in qualche caso, dqE
2= dqS
2 + dqC
2.
Problema: come si può quantificare l'allargamento dqC e valutare N?
- Si prenda un cristallo finito, di dimensione t nella direzione normale ai piani dhkl
- Se ci sono m piani, mdhkl = t
- Immaginiamo che il cristallo sia in condizioni di riflessione (del 1° ordine) di Bragg, per cui: l = 2dhklsenq
- Tra i piani 0 ed 1, il DC.O. è 2dhklsenq = l
- Tra i piani 0 e 2, il DC.O. è 4dhklsenq = 2l
- Tra i piani 0 e k, il DC.O. è multiplo di 2dhklsenq = multiplo di l
Ovvero: tutti i piani sono in condizioni di interferenza costruttiva
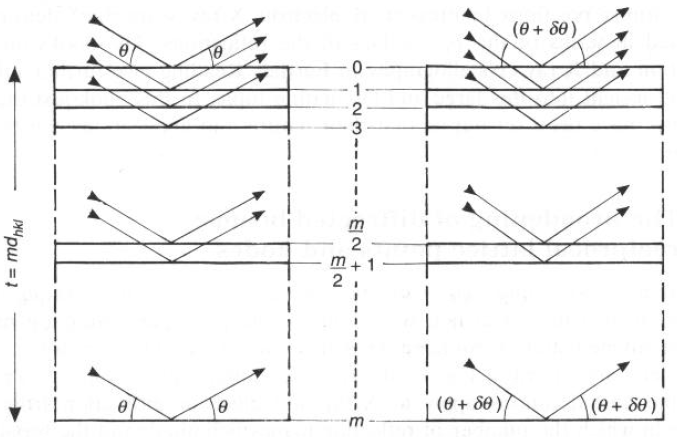
- Immaginiamo che il cristallo sia QUASI in condizioni di riflessione (del 1° ordine) di Bragg, per cui: l = 2dhklsenq
- Tra i piani 0 ed 1, il DC.O. è QUASI 2dhklsenq = l (Interferenza costruttiva)
-
Tra i piani 0 e 2, il DC.O. è QUASI 4dhklsenq = 2l (Interferenza un po' meno costruttiva)-
Tra i piani 0 e k, il DC.O. finisce per non essere più QUASI multiplo di 2dhklsenq = QUASI multiplo di l, ma, più k si allontana da 0, si rischia che ci siano piani con DC.O. semintero!
-
Accoppiamo i raggi diffratti dal piano 0 e dal piano m/2:-
All'angolo di Bragg: (m/2)l = (m/2)2dhklsenq (Interferenza costruttiva)-
Si ha interferenza distruttiva all'angolo (q + dq) quando invece: (m/2)l + l/2= (m/2)2dhklsen(q + dq)-
Questo è anche l'angolo per cui interferiscono fuori fase i piani (1 e m/2+1); (2 e m/2+2), etc.-
In pratica, (m/2)l + l/2= (m/2)2dhklsen(q + dq) ci d' la condizione angolare per cui i raggi diffratti danno interferenza distruttiva su tutto il cristallo.(m/2)
l + l/2 = (m/2)2dhklsen(q + dq) = (m/2)2dhkl(senqcosdq + cosqsendq)Per piccoli angoli d
q, cosdq - 1 e sendq - dq(m/2)
l + l/2 = (m/2)2dhklsenq + (m/2)2dhklcosq dq ovvero:l
/2 = (m/2)2dhklcosq dq l = (m)2dhklcosq dq = 2tcosq dq da cui: 2dq = l/tcosq Equazione di Scherrerspesso modificata in 2d
q = kl/tcosq e k - 0.9 (o meno).Spesso si associa alla larghezza di un picco la FWHM o
b - 2dq
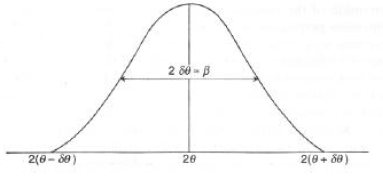
2d
q = b = l/tcosq, o: thkl = l/bcosqhklNella costruzione di Ewald, per un nodo di dimesioni NON puntiformi, ma spesso t (nella direzione
d*hkl):Dato che |
d*hkl| = d*hkl = 2senq/ld
(d*hkl) = d(2senq/l) = 2cosq/l dqOvvero:
d
(d*hkl) = 2cosq/l l/2tcosq = 1/t = t-1
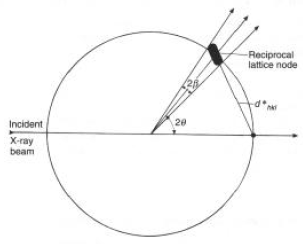
- Le dimensioni del nodo lungo (hkl) sono il reciproco dello spessore del cristallo in (hkl)
- Corollario: la forma tridimensionale del nodo è determinata dalla forma tridimensionale del cristallo!
- Cristalli 3D infiniti i nodi sono puntiformi
- Cristalli 2D infiniti i "nodi" sono linee strutture a strati
- Cristalli 1D infiniti i "nodi" sono piani polimeri stirati
- Oggetti 0D (amorfi, gas) non ci sono nodi!
Portale "Ingegneria e
Campanologia" -
Autore -
Sommario
- Mappa del Sito -
Home
Bib-TS-081 - Prof. N. Masciocchi - Dispense del Corso di Laurea in Chimica - Insegnamento di strutturistica chimica
Bib-TS-082 - C.Hammond - The Basics of Crystallography and Diffraction - Ed. International Union of Crystallography and Oxford University Press, 240 pg. (Ed. italiana: Zanichelli)
Bib-TS-083 - J.P.Glusker & K.N.Trueblood - Crystal Structure Analysis: A Primer - Oxford University Press, 220 pg. (non tradotto).