Portale "Ingegneria e Campanologia" - Autore - Sommario - Mappa del Sito - Home
Strutturistica Chimica
AREA I - ARTE TECNICO-SCIENTIFICA (ATS)
Cap. ATS-F02 - Chimica - Pag. ATS-F02.14
Gli argomenti trattati sono stati inseriti da Ing. Arch. Michele Cuzzoni nel 2012 - © Copyright 2007- 2024 - e sono desunti dalla documentazione indicata in Bibliografia a fondo pagina
La distanza che separa due piani contigui (misurata lungo la normale ad essi) si può calcolare sapendo che, per un piano di indici (hkl), essa coincide con la sua distanza dall’origine (dove passa un altro piano!):
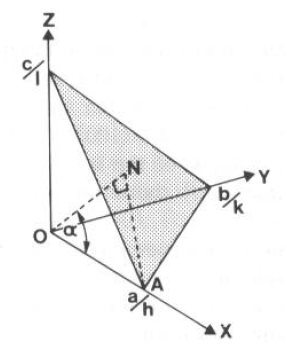
· Distanza da O = |ON|;
· Angolo AON = a;
· Angolo ONA = 90° per costruzione
· |OA| cos a = |ON|
· (a/h) cos a = dhkl
· cos a = (h/a) dhkl
· Analogamente:
· cos b = (k/b) dhkl
· cos g = (l/c) dhkl
Per assi ortogonali: cos2 a + cos2 b + cos2 g = 1 (Pitagora)
(h/a)2 d2hkl + (k/b)2 d2hkl + (l/c)2 d2hkl = 1
Per un cristallo cubico: 1/d2hkl = 1/a2 * (h2+k2+l2)
I concetti di piano reticolare e di distanza interplanare sono alla base della definizione di reticolo reciproco e dell’equazione di Bragg:
nl = 2dhkl sin q
dove
n è l’ordine di una riflessione,
l è la lunghezza d’onda della radiazione incidente,
dhkl è la separazione tra i piani riflettenti
q è l’angolo di incidenza e riflessione.
Nella legge di Bragg è fondamentale distinguere tra piani reticolari e piani riflettenti:
· Tranne nel caso di reticoli NON primitivi, gli
indici di Miller NON hanno fattori comuni;· Piani riflettenti distinti POSSONO avere indici con fattori comuni, detti
indici di Laue (indicati SENZA parentesi…);· Che relazione esiste fra gli indici di Miller e quelli di Laue?
Per il piano reticolare (111) posso avere fisicamente più riflessioni:
1. Prim’ordine: 1l = 2d111 sin q1
2. Second’ordine: 2l = 2d111 sin q2
3. Etc… nl = 2d111 sin qn
Per ogni ordine di riflessione, posso riscrivere la relazione di Bragg:
1
l = 2(d111/n) sin qn
· Ovvero: riflessioni di ordine n possono essere viste come riflessioni del prim’ordine di piani (reticolari non esistenti) con distanza interplanare (d111/n) (indici di Laue nnn)
· Piani di tipo 222 non sono piani reticolari, ma solo uno su due passa per i nodi del reticolo
· Per abitudine, in esperimenti di diffrazione, si tende a dimenticare la distinzione tra (hkl) ed hkl. Il riflesso 2h,2k,2l è comunemente inteso come quello derivante dal piano hkl (n = 2) o, il che è equivalente, dal piano ‘fittizio’ 2h,2k,2l per n=1
· In reticoli NON primitivi: I piani (100) e (200) sono ambedue piani reticolari distinti; I riflessi 100 e 200 derivano da interferenza per n = 1 e n = 2 della stessa distanza d100 (o, il che è equivalente, da distanze distinte d100 e d200 (ma questa volta i piani (200) non sono fittizi!)
· La legge di ZONA (o legge di Weiss):
Se un piano (hkl) giace in una zona [uvw] (ovvero, se la direzione [uvw] è parallela al piano (hkl), allora hu + kv + lw =0
· Asse di zona come intersezione tra due piani:
La linea di intersezione tra due piani in una zona (h1k1l1) e (h2k2l2) costituisce l’asse di zona [uvw], dove:
u = (k1l2-k2l1); v = (l1h2-l2h1); w = (h1k2-h2k1);
Mnemonicamente:

u = det(M1) = +k1l2 – k2l1, etc.
· Piano parallelo a due direzioni:
Date due direzioni [u1v1w1] e [u1v1w1], il piano parallelo ad ambedue si costruisce in modo analogo con:
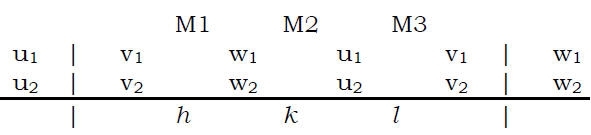
h = det(M1) = +v1w2 – v2w1, etc.
· La regola dell’addizione:
Siano dati due piani (h1k1l1) e (h2k2l2) che giacciono in una zona. L’indice di Miller di qualsiasi altro piano (HKL) in zona con questi piani è dato da:
H = (
mh1 + nh2); K = (mk1 + nk2); L = (ml1 + nl2),con m e n interi (piccoli);
Ovvero: (HKL) è combinazione lineare di (h1k1l1) e (h2k2l2)
Esempio:
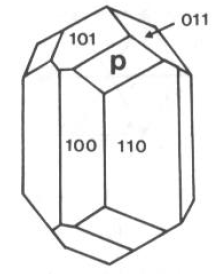
Problema:
Determinare l’indice di Miller del piano P, che giace sia nella zona determinata da (100) e (011), che in quella determinata da (110) e (101).
L’indice di Miller di P deve essere ottenibile come combinazione lineare sia della prima coppia che della seconda:
A tentativi: (101) + (110) = (211) (m=1, n=1)
(011) + 2(100) = (211) (m=1, n=2)
I reticoli romboedrici ed esagonali sono basati sull’impilamento di reticoli planari esagonali in sequenza ABCABC… (romboedrico) o AAA.. (esagonale semplice).
Per convenzione, gli strati esagonali stanno alla ‘base’ della cella (assi a e b), mentre l’asse c ne è perpendicolare, e parallelo alla direzione di impilamento.
Si possono usare almeno TRE diverse celle di riferimento:
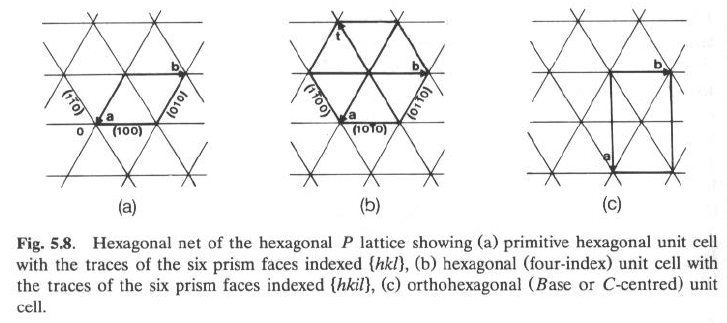
Come in (a): cella esagonale primitiva, con assi a e b di lunghezza uguale e con angolo g = 120°. Questa scelta semplice NON rivela la simmetria esagonale del reticolo.
P.es., le facce laterali (equivalenti per simmetria! – forma {100} ) di un prisma esagonale retto hanno indici di Miller del tipo:
(100), (010), (1-10) (più le centrosimmetriche),
facendole sembrare di tipo e natura diverse!
Per superare questa apparente incongruenza, si introduce un QUARTO asse (NON indipendente!), chiamato u, a 120° sia da x che da y.
I quattro assi di Miller-Bravais x,y,u,z sono definiti da vettori di cella a, b, t, c, e implicano indici di Miller-Bravais di tipo (hkil)
Si introduce così una cella esagonale primitiva a 4 assi (b) con indici (hkil) o (hk.l), dove, per costruzione, h + k + i = 0, ovvero i = - (h+k)
· La forma {10-10} comprende (10-10), (01-10); (1-100) (più le centrosimmetriche!)
· La forma {10.0} comprende: (10.0), (01.0); (1-1.0) (più le centrosimmetriche!)
La terza scelta, © prevede una cella ortoesagonale (ortorombica con a/b=Ö3), che non evidenzia la simmetria esagonale del reticolo, ma può essere usata quando piccole distorsioni dall’idealità fanno scendere la simmetria da vera esagonale a reale ortorombica.
Anche per gli assi di zona si usano 4 indici (simboli di Weber), del tipo [UVTW], tale per cui U + V + T = 0
Come si passa da [uvw] a [UVTW]?
U = 1/3 (2u-v); V = 1/3 (2v-u); T = -U+V; W = w
Con questa convenzione, gli assi x, y ed u si trasformano in: x = [2-1-10]; y = [-12-10]; u = [-1-120];
La trasformazione inversa da [UVTW] a [uvw] si ottiene con: u = (U-T); v = (V-T); w = W;
Con gli indici di Miller-Bravais (piani) e simboli di Weber (assi), la legge di Weiss diventa:
hU + kV + iT + lW = 0
In conclusione, un simbolo del tipo (111) per un sistema trigonale od esagonale può significare più cose, a seconda che il riferimento sia:
· la cella primitiva esagonale (tipo a);
· la cella ortoesagonale C (centrata in ab ) (tipo c);
· la cella esagonale a 4 assi (tipo b), e significa (11-21), ovvero (11.1)
NON SOLO per i sistemi trigonali ed esagonali sono necessarie relazioni geometriche che trasformano celle, indici e simboli vari, dato che, p.es., alcune scelte convenzionali possono non essere adottate da tutti;
Es. storico: per anni l’asse unico del sistema monoclino era c, (non b)
Es. comune: Uso di Monoclino I, al posto di Monoclino C
Ci aiuta in queste trasformazioni l’algebra matriciale.
Esempio:
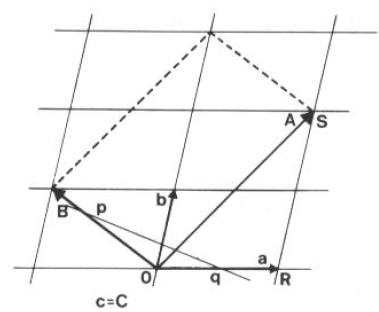
Due diverse celle possono descrivere il reticolo bidimensionale della figura (immaginata con il terzo asse perpendicolare al foglio):
I cella: a, b, c II cella: A, B, C
Ovviamente: c = C
Ma come sono correlati a,b con A, B?

Per la I cella (abc), siano (hkl) e [uvw] piani ed assi;
Per la II cella (ABC), siano (HKL) e [UVW] piani ed assi;
Il piano generico di traccia pq sia il primo piano fuori dall’origine:
Per definizione, pq ha intercette a/h su a, A/H su A, b/k su b, etc.
Ma: h è anche il numero di piani che sono intercettati lungo il vettore a
H è il numero di piani intercettati lungo A; etc.
h è il numero di piani intercettati lungo a (da O a R)
2k è il numero di piani intercettati lungo 2b (da R a S)
Quindi, il numero di piani intercettati lungo 1a + 2b (da O a S) è h+2k; dato che A = 1a + 2b, H è proprio h+2k;
Si deriva pertanto:
H = 1h + 2k + 0l
K = -1h + 1k + 0l
L = 0h + 0k + 1l
Gli indici di Miller si trasformano in modo UGUALE agli assi di cella.
Si adotta la convenzione di usare VETTORI-RIGA per gli indici:

Preso un generico vettore r = ua + vb + wc = UA + VB + WC
r = ua+vb+wc = U(1a+2b+0c) + V(-1a+1b+0c) + W(0a+0b+1c)
e riordinando: u = 1U + -1V + 0W
v = 2U + 1V + 0W
w = 0U + 0V + 1W
Le direzioni si trasformano in modo UGUALE agli assi di cella, se usiamo VETTORI-COLONNA:

La STESSA matrice T collega:
· Indici di Miller, famiglie di piani, dalla I alla II cella [righe]
· e direzioni, assi, zone dalla II alla I cella [colonne]
Le trasformazioni inverse sono date dalle matrici INVERSE
L’inversa della matrice T è T-1:

Nota: Il determinante della matrice T è det(T) = 3; ciò significa che la cella II, generata dalla I secondo:
(ABC)colonna = T(abc)colonna ha un volume 3 volte superiore!
Ricapitolando:
(ABC)colonna = T(abc)colonna (abc)colonna= T-1(ABC)colonna
(HKL)riga = (hkl)rigaT (hkl)riga = (HKL)rigaT-1
(UVW)colonna = T-1(uvw)colonna (uvw)colonna= T(UVW)colonna
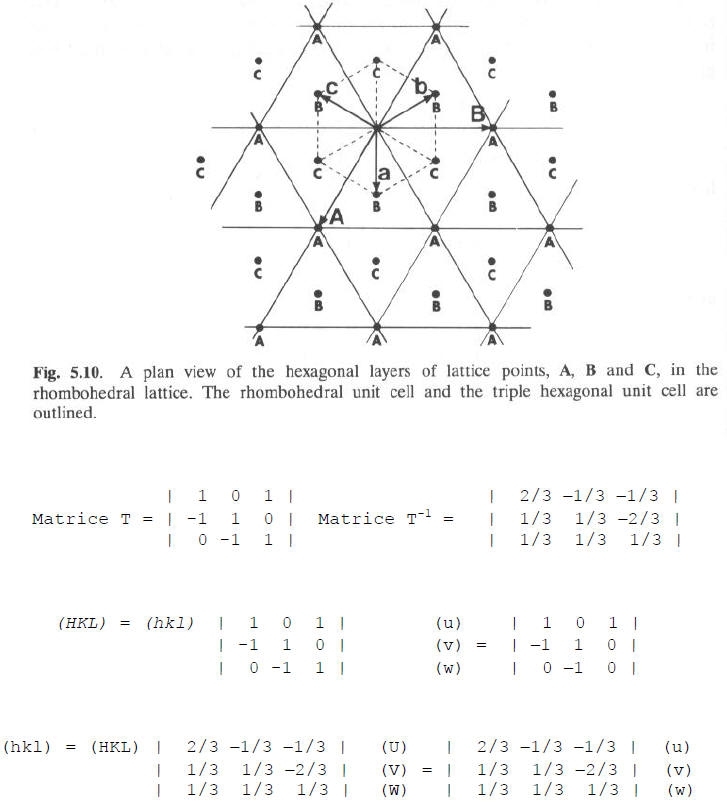
Trasformazione speciale: da romboedrico ad assi equiinclinati: a,b,c (a,a,a) in esagonale non primitivo R: A, B, C (90,90,120)
Portale "Ingegneria e
Campanologia" -
Autore -
Sommario
- Mappa del Sito -
Home
Bib-TS-081 - Prof. N. Masciocchi - Dispense del Corso di Laurea in Chimica - Insegnamento di strutturistica chimica
Bib-TS-082 - C.Hammond - The Basics of Crystallography and Diffraction - Ed. International Union of Crystallography and Oxford University Press, 240 pg. (Ed. italiana: Zanichelli)
Bib-TS-083 - J.P.Glusker & K.N.Trueblood - Crystal Structure Analysis: A Primer - Oxford University Press, 220 pg. (non tradotto).