Portale "Ingegneria e Campanologia" - Autore - Sommario - Mappa del Sito - Home
Fisica Acustica
AREA I - ARTE TECNICO-SCIENTIFICA (ATS)
Cap. ATS-E01 - Fisica - Pag. ATS-E01.05
Gli argomenti trattati sono stati inseriti da Ing. Arch. Michele Cuzzoni nel 2008 - © Copyright 2007- 2024 - e sono desunti dalla documentazione indicata in Bibliografia a fondo pagina
D’Alembert fu il primo che presentò una soluzione per integrare l’equazione:
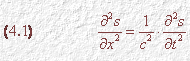
che caratterizza le vibrazioni delle molecole in un mezzo elastico, dove c è la velocità di propagazione dell’onda. Pertanto la 4.1 prende anche il nome di “equazione di D’Alembert”.
D’Alembert affrontò il problema studiando le forme assunte da una corda vibrante vincolata agli estremi. In particolare, mostrò che le configurazioni assunte dalla corda sono infinite: la configurazione sinusoidale, dimostrata da Bernoulli, è una delle tante.
La funzione s(t, x) che descrive le infinite configurazioni della corda – così dimostrò D’Alembert – è data da:
![]()
dove f1 e f2 sono due funzioni arbitrarie, da valutare mediante le condizioni al contorno e le condizioni iniziali del problema. In altre parole, la soluzione generale è data dalla somma di due onde viaggianti, una progressiva (f1) e l’altra regressiva (f2).
Data la sua complessità, l’equazione di d’Alembert può essere integrata con gli ordinari metodi del calcolo solo in tre casi: quello di onda piana progressiva (come si è ipotizzato nei tre paragrafi precedenti, allorché abbiamo considerato la propagazione dell’onda in una sola direzione entro un mezzo di lunghezza indefinita), di onda sferica progressiva, e di onda piana stazionaria (quando il mezzo dove si manifesta la propagazione del moto vibratorio è di lunghezza definita). Per la risoluzione di casi più complessi si ricorre a metodi numerici.
Il problema fu affrontato da D’Alembert mediante una sostituzione di variabili; noi lo affronteremo invece mediante il procedimento di separazione delle variabili, che ci consente di sviluppare in forma compendiaria un ragionamento alquanto complesso.
Poiché la funzione risolutiva della 4.1 sarà del tipo:
s = s(t, x)
poniamo:
s(t, x) = T(t)·X(x)
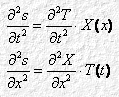
Quindi, sostituendo nella 4.1:
![]()
Infine, separando le variabili:
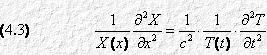
Poiché X e T sono due funzioni indipendenti l’una dall’altra, i due membri della (4.3) equivalgono a una costante, che chiameremo “– k2”. Otteniamo così due equazioni differenziali ordinarie, a una sola variabile:
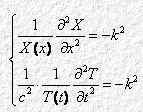
ovvero:
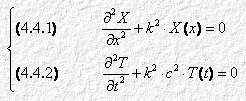
Per integrare la 4.4.1, scriviamone l’equazione caratteristica associata, sostituiamo cioè: al posto della derivata seconda, a2; al posto della derivata prima (che peraltro qui non c’è), a; al posto della variabile, 1. Otteniamo allora:
a2 + k2 = 0
Di qui ricaviamo:
a = ± j k
dove j è l’unità immaginaria. Possiamo allora scrivere la soluzione della 4.4.1 nella forma:
X(x) = Aejkx + Be–jkx
o anche:
X(x) = E sin(kx + f)
Analogamente per la 4.4.2 si ha:
a2 + k2c2 = 0
Di qui ricaviamo:
a = ± j kc
Possiamo allora scrivere la soluzione della 4.4.2 nella forma:
T(t) = Cejkct + De–jkct
o anche:
T(t) = F sin(kct + y)
Pertanto la soluzione della 4.1 sarà:
s(t, x) = T(t)·X(x) = G· sin(kx + f)· sin(kct + y)
Osserviamo a questo punto che kc ha le dimensioni di una “pulsazione” (rad/s), pertanto al suo posto scriviamo w, che è – appunto – il simbolo della pulsazione:
s(t, x) = G· sin(kx + f)·sin(wt + y)
Per semplificare questa espressione, ipotizziamo che per t = 0 e x = 0 sia s = 0 (per esempio, nel caso di un’asta vincolata a un’estremità, possiamo porre l’origine dell’asse x su quell’estremità e cominciare calcolare i tempi nel preciso istante in cui l’asta viene sollecitata a vibrare). In tal caso f = y = 0. Possiamo allora scrivere:
(4.5) s(t, x) = G·sin kx · sin wt
Ricordando inoltre la relazione tra velocità di propagazione di un fenomeno ondoso, frequenza f e lunghezza d’onda l, possiamo dare un significato a k:
k = w/c = 2pf / f·l = 2p/l
Il parametro k prende il nome di “numero d’onda”.
La 4.5 è dunque la soluzione generale della 4.1. Per poterla confrontare con la 4.2, la soluzione proposta da D’Alembert, dobbiamo operare ancora una trasformazione. Applichiamo allora le formule di addizione della trigonometria:
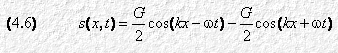
Per determinare G e w nella 4.6 (o, più semplicemente, nella 4.5) occorre sviluppare alcune considerazioni sulle condizioni al contorno: per esempio, nel caso di una sbarra non vincolata alle estremità, imponiamo che per x = L (la lunghezza della sbarra) la deformazione (s/x) sia uguale a zero. Facendo i calcoli, si ottiene un insieme infinito di valori della pulsazione wi, ai quali corrispondono le relative frequenze naturali del sistema fi, secondo la formula wi = 2p fi. A ogni frequenza fi corrisponde un numero d’onda ki = wi / c.
Sempre in base a considerazioni di contorno, si dimostra che – nel caso di onde longitudinali piane in una colonna d’aria di lunghezza indefinita – l’espressione di s(x, t) presentata nella 4.6 manca del secondo termine: si ha una sola onda viaggiante, progressiva. Inoltre, in questo caso il sistema non ha frequenze naturali.
Portale "Ingegneria e
Campanologia" -
Autore -
Sommario
- Mappa del Sito -
Home
Bib-TS-067 - Ing. Arch. Michele Cuzzoni - Appunti di Fisica 2: Acustica – Facoltà di Ingegneria, Pavia - A.A. 1995-1996
Bib-TS-068 - Il Nuovo Colombo - Manuale dell'Ingegnere - Volume primo - 83^ edizione - Ed. Ulrico Hoepli Milano - 1997 Ristampa 2001